数字逻辑设计及应用 -- 数制与编码

                                               数制与编码

       在信息世界中，信息分为数值信息和非数值信息，我们学习的数字系统只处理数字信号0,1，所以在数字系统中需要将任意信息用（0,1）表达。

       用（0,1）表达数量：数制 -- 二进制

       用（0,1）表达不同对象：编码

      下面讲解按位计数制

      特点：

             1、采用基数，R进制的基数是R

             2、基数确定数符的个数

                 eg:十进制的数符为：0、1、2、3、4、5、6、7、8、9，个数为10；

                      二进制的数符为：0、1，个数为2

            3、逢基数进一

              如：

                       考虑到数字系统的成本和性能，数字电路中多使用二进制来表示信息。

                                                               十进制、二进制 、八进制、十六进制转换表

---

                                  

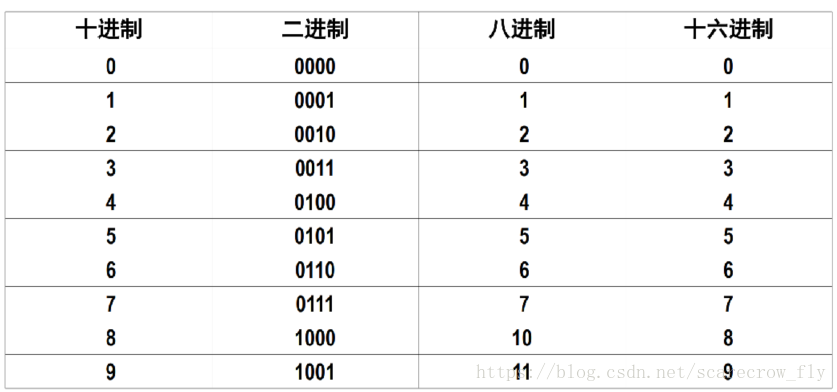
                                    二进制和八进制、十六进制之间的转换方法

•    位数替换法

         保持小数点不变，以小数点为起点，向左、向右分别取位数，每位八进制对应3位二进制数，每位十六进制数对应4位二进制数，在最高有效位和最低有效位前/后方可以补零。

         反之，八进制/十六进制转换为二进制也是同理，值得注意的是，转换之后的数值，最高有效位之前的零和最低有效位之后的零不写。

       

---

                                    

                                     任意进制和十进制之间的转换方法

•  权位展开相加

        当其他进制数转换为十进制的时候，以小数点为界，向左各位数上的数值分别乘以基数的0次幂、1次幂、2次幂...向右各位数上的数值分别乘以基数的-1次幂、-2次幂...

        eg：二进制数：（101.01） =  1*2^2+0*2^1+1*2^0+0*2^(-1)+1*2^(-2) = 4+0+1+0+0.25 = 5.25(十进制数)

---

                                     十进制和二进制之间的转换方法

•    整数部分

        1、除2取余，直到商为0为止，逆序排列

       

        2、按权

       156  转换为2进制数：

       ① 比较与156相近的2的幂次数   128 = 2^7

       ② 156-128=28，再返回第一步，比较与28相近的2的幂次数   16  = 2^4

       ......

       得到：2^7 + 2^4 + 2^3 + 2^2

       将二进制按权相标

       分别为， n , (n-1),......7,6,5,4,3,2,1,0

       对号入座，有幂次数的位数所在的数值为1，其余为0

       则二进制数为：10011100

•    小数部分：乘2取余，顺序排列

        具体做法：用2乘十进制小数，得道积，将积的整数部分取出，再用2乘以余下的小数部分，得到积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或达到要求的精度为止，然后将取出的整数部分开始按次序取出即为二进制的小数部分.

        eg:

 

  附上进制转换工具

   https://tool.lu/hexconvert/