本文详细介绍了归并排序的原理与代码实现，包括其在计算逆序数和小和问题上的应用。通过实例演示，展示了如何手撕归并排序算法，并探讨了二分查找的非递归和递归版本。同时，前缀树（Trie树）的基础操作及实际场景也被深入剖析。
一 归并排序
归并排序也是分治法一个很好的应用，先递归到最底层，然后从下往上每次两个序列进行归并合起来，是一个由上往下分开，再由下往上合并的过程。
而对于每一次合并操作，对于每一次 merge 的操作过程如下：
1、准备一个额外的数组（help），使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2、设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3、比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4、重复步骤3直到某一指针达到序列尾；
5、将另一序列剩下的所有元素直接复制到合并序列尾；
看下面的例子合并过程如下：
1、归并排序的代码实现
public class Test {
public static void main(String[] args) {
int[] arr = {50,10,90,30,70,40,80,60,20};
mergeSort(arr,0,arr.length-1);
for(int i=0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
public static void merge(int[] arr,int low,int mid,int high){
int[] tmp = new int[high-low+1];
int i = 0;
int j = low,k = mid+1; //左边序列和右边序列起始索引
while(j <= mid && k <= high){
if(arr[j] < arr[k]){
tmp[i++] = arr[j++];
}else{
tmp[i++] = arr[k++];
}
}
//若左边序列还有剩余，则将其全部拷贝进tmp[]中
while(j <= mid){
tmp[i++] = arr[j++];
}
while(k <= high){
tmp[i++] = arr[k++];
}
for(int t=0;t<i;t++){
arr[low+t] = tmp[t];
}
}
public static void mergeSort(int[] arr,int low,int high){
if(low<high){
int mid = (low+high)/2;
mergeSort(arr,low,mid); //对左边序列进行归并排序
mergeSort(arr,mid+1,high); //对右边序列进行归并排序
merge(arr,low,mid,high); //合并两个有序序列
}
}
}
2、逆序对数问题，是归并排序的一个应用
另外再补充一个LintCode532Reverse Pairs归并排序求解逆序数的问题:
这个的关键在于，在合并 l ~ mid 和 mid+1~r 的过程中，只要 arr[p1] > arr[p2]，则 arr[p2] 和 arr[p1 ~ mid] 都能组成逆序对，所以我们每次都可以加上 mid - p1 + 1 个数，故可以方便求出逆序数对数。
public class test {
public static void main(String[] args) {
int[] arr = {7,5,6,4};
System.out.print(mergeSort(arr,0,arr.length-1));
}
public static long merge(int[] arr,int low,int mid,int high){
int[] tmp = new int[high-low+1];
int i = 0;
int sum=0;
int j = low,k = mid+1; //左边序列和右边序列起始索引
while(j <= mid && k <= high){
if(arr[j] < arr[k]){
tmp[i++] = arr[j++];
}else{
sum += mid-j+1;
tmp[i++] = arr[k++];
}
}
//若左边序列还有剩余，则将其全部拷贝进tmp[]中
while(j <= mid){
tmp[i++] = arr[j++];
}
while(k <= high){
tmp[i++] = arr[k++];
}
for(int t=0;t<i;t++){
arr[low+t] = tmp[t];
}
return sum;
}
public static long mergeSort(int[] arr,int low,int high){
if(low>=high)
return 0;
else{
int mid = (low+high)/2;
return mergeSort(arr,low,mid)
+mergeSort(arr,mid+1,high)
+merge(arr,low,mid,high);
}
}
}
3、小和问题
还有一个题目就是小和问题: 具体的问题和上面的逆序数差不多。
public class test {
public static void main(String[] args) {
int[] arr = {1,3,4,2,5};
System.out.print(mergeSort(arr,0,arr.length-1));
}
public static long merge(int[] arr,int low,int mid,int high){
int[] tmp = new int[high-low+1];
int i = 0;
int sum=0;
int j = low,k = mid+1; //左边序列和右边序列起始索引
while(j <= mid && k <= high){
if(arr[j] < arr[k]){
sum += arr[j]*(high-k+1);
System.out.println(arr[j]*(high-k+1));
tmp[i++] = arr[j++];
}else{
tmp[i++] = arr[k++];
}
}
//若左边序列还有剩余，则将其全部拷贝进tmp[]中
while(j <= mid){
tmp[i++] = arr[j++];
}
while(k <= high){
tmp[i++] = arr[k++];
}
for(int t=0;t<i;t++){
arr[low+t] = tmp[t];
}
return sum;
}
public static long mergeSort(int[] arr,int low,int high){
if(low>=high)
return 0;
else{
int mid = (low+high)/2;
return mergeSort(arr,low,mid)
+mergeSort(arr,mid+1,high)
+merge(arr,low,mid,high);
// mergeSort(arr,low,mid); //对左边序列进行归并排序
// mergeSort(arr,mid+1,high); //对右边序列进行归并排序
// merge(arr,low,mid,high); //合并两个有序序列
}
}
}
本文主要讲述面试现场常遇见的手撕代码题：二分查找。虽然代码很好理解也很简单，但是感觉只有多练，多理解才能真的掌握。千万不要眼高手低，稳扎稳打才是王道。
二. 二分查找
二分法是算法里的一个重要方法，很多算法都可以用这个思想去解决，所以一定要掌握。
要使用它有一个前提条件：数组必须有序，递增或者递减；
二分查找的优点：比较次数较少、查找速度快、平均性能好；
二分查找的缺点：待查表为有序表，插入困难；由此延伸为顺序结构中，插入与删除比较困难；
二分查找的思想：
- 首先确定整个查找区间的中间位置mid = （end - start）/2；
- 用待查关键字值与中间位置的关键字值进行比较，若相等，则返回中间下标；
若不相等，有两种情况：
- 若array[mid] > key：查找范围缩小为左半区域，具体表现为：statrt不变，end = mid - 1；
- 若array[mid] < key：查找范围缩小为右半区域，具体表现为：end不变，start = mid + 1；
- 对确定的缩小区域再进行折半公式，重复以上步骤！
注意的点：在使用if时一定要确定好是否还可以继续if的条件，那就是：start ，只有在这个条件底下，才可以查询！！！
1.非递归版本
public class BinarySearch {
/**
* 非递归实现
* @param array ： 有序数组
* @param key ：需要查找的数
* @return ：返回 key 在数组 array 中的下标
*/
public static int binarySearch(int[] array, int key){
if(array.length < 1){
return -1;
}
int mid;
int start = 0;
int end = array.length - 1;
while(start <= end){
// 为了防止int溢出，最好这样写
mid = (end - start) / 2 + start;
if(key > array[mid]){
start = mid + 1;
}else if(key < array[mid]){
end = mid - 1;
}else{
return mid; // 找到了
}
}
return -1; // 没找到
}
public static void main(String[] args) {
int[] arr = {1,2,3,4,5};
System.out.println(binarySearch(arr,3));
}
}
2.递归版本实现
public class BinarySearchWithRecursion {
public static int binarySearch(int[] arrs,int key,int low,int high) {
if(low<=high) {
int mid = (high+low)/2;
if(arrs[mid]==key)
return mid;
else if(arrs[mid]<key)
return diguibinarySearch(arrs,key,mid+1,high);
else
return diguibinarySearch(arrs,key,low,mid-1);
}
return -1;
}
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6};
System.out.println(binarySearch(arr, 6));
}
}
三 前缀树：Prefix Tree
- 前缀树又叫字典树、Trie 树，单词查找树或键树，是一种多叉树结构。
- 前缀树的功能很强大，比如有一个字符串数据，我们要从查找其中以“hell”开头的(设置一个passN)，或者以"ive"结尾的字符的个数等等操作。我们只需要在定义前缀树的时候加上相应得数据项就可以了。
- 建议：字母用边表示，不要塞到节点里【具体看代码实现】。
3.1 前缀树题目举例力扣 208：一个字符串类型的数组 arr1，另一个字符串类型的数组 arr2
题目1、 arr2中有哪些字符，是arr1中出现的？请打印。
- 返回树中有多少个要求查找的单词 public int search(String word) 的变体。
题目2、arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印。
- 有多少单词以pre为前缀 public int prefixNumber(String pre)的变体。
题目3、arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印arr2中出现次数最大的前缀。
- 有多少单词以pre为前缀 public int prefixNumber(String pre)，找最大的个。
3.2 前缀树的 insert、delete、search、prefixNum 方法
- 几种方法的代码相似度很高，前半部分基本一样，都是从 root 开始遍历；
- 假设刚开始我们，有一个空节点，现在我们有一个操作，往这个空的节点上insert字符串“abc”, 那么我们按照下面的步骤insert：
- process: 首先看当前节点有没有指向字符'a'的路径，没有的话就创建指向'a'的路径，否则滑过到下一个字符，同样是看看有没有到该字符的路径。一直遍历完字符，并且都创建好了路径。如下图所示：
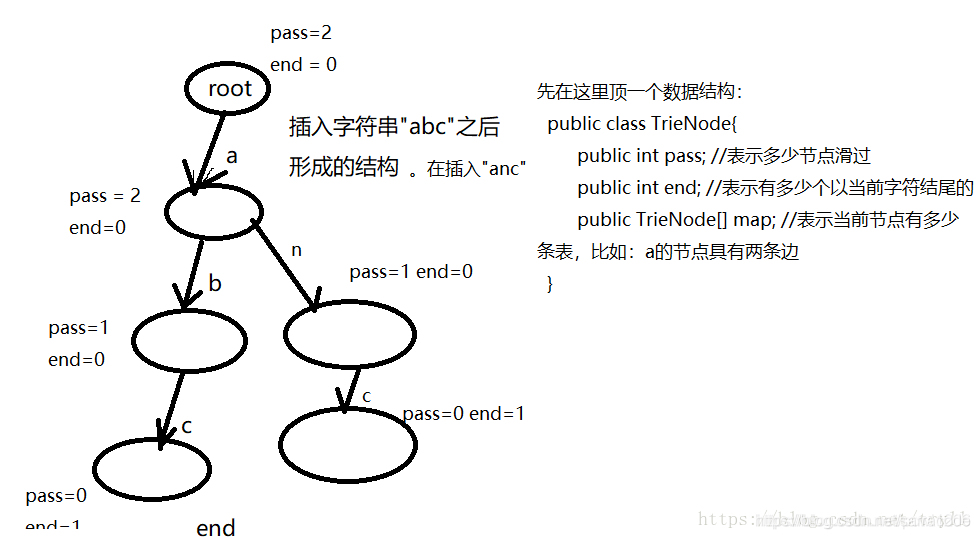
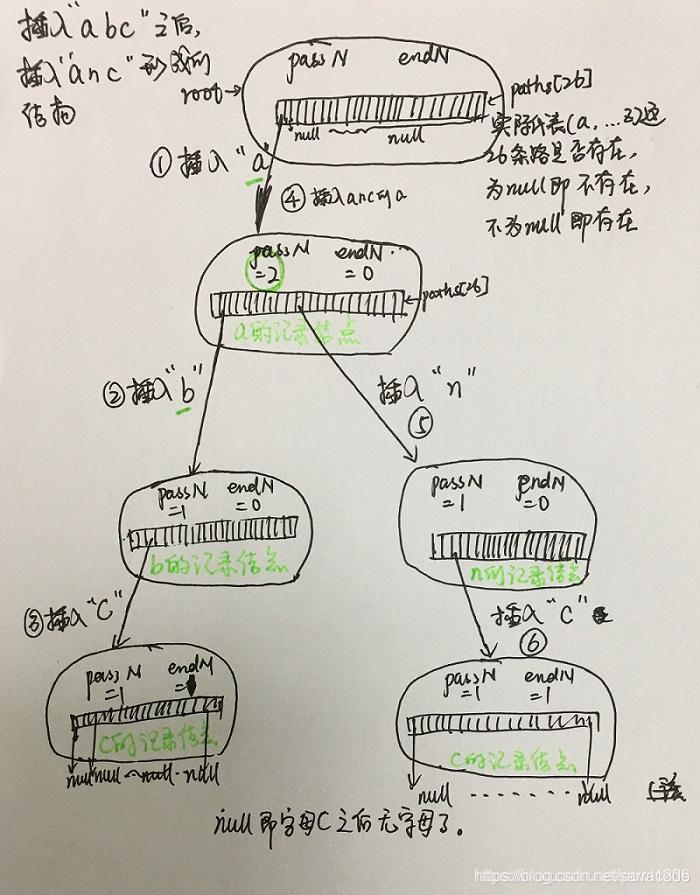
代码实现
package com.offer.foundation.class5;
/**
* @author pengcheng
* @date 2019/3/29 - 22:34
* @content: Trie树的基本操作的实现
*/
public class TrieTree {
public static class TrieNode{
private int passNum; // 表示有多少个字符串经过该节点
private int endNum; // 表示有多少个字符串以该节点结尾
private TrieNode[] paths; // 存储的是该节点到下一级所有节点的路径是否存在
public TrieNode(){
passNum = 0;
endNum = 0;
paths = new TrieNode[26]; // 假设只有26个小写字母，即每一个节点拥有26条可能的路径
}
}
private TrieNode root; // 不管什么操作，都是从根节点开始的，所以要记录根节点
public TrieTree(){
// Trie树的初始化
root = new TrieNode();
}
// 往trie树中插入一个字符串
public void insert(String word){
if(word == null){
return;
}
char[] chars = word.toCharArray();
TrieNode node = root;
int index = 0; // index值：0-25 对应 a-z
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a'; // 计算该字符在当前节点的那条路径上
// 判断该路径是否已经存在
if(node.paths[index] == null){
node.paths[index] = new TrieNode(); // 如果路径不存在，则创建它
}
// 路径已经存在的话，就继续向下走
node = node.paths[index];
node.passNum++; // 划过当前节点的字符串数+1
}
node.endNum++; // 遍历结束了，记录下以该字母结束的字符串数+1
}
// 删除一个字符串
public void delete(String word){
// 删除之前，先判断有没有
if(search(word) == 0){
return;
}
char[] chars = word.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a';
// 注意 --
if(--node.paths[index].passNum == 0){
// 如果遍历到某个节点时，将其index处passNum减1后等于0，则说明没有其他字符串经过它了，直接将其设置为null
node.paths[index] = null;
return;
}
node = node.paths[index]; // 继续向下遍历
}
node.endNum--; // 遍历完了，删除了整个单词，则将以该单词最后一个字符结尾的字符串的数目减1
}
// 在trie树中查找word字符串出现的次数
public int search(String word){
if(word == null){
return 0;
}
char[] chars = word.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a';
if(node.paths[index] == null){
return 0; // 不存在
}
node = node.paths[index]; // 到达了该字母记录的节点路径，继续往下走
}
// 整个单词的所有字母都在树中，说明单词在树中，返回该单词最后一个字符的endNum
return node.endNum;
}
// 返回有多少单词以pre为前缀的
public int prefixNum(String pre){
if(pre == null){
return 0;
}
char[] chars = pre.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a';
if(node.paths[index] == null){
return 0; // 不存在
}
node = node.paths[index]; // 继续向下找
}
return node.passNum; // 找到pre最后一个字符的passNum值
}
}
扫一扫
684
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
