原博:https://blog.youkuaiyun.com/iyuanshuo/article/details/80112211
典型的动态规划问题。
首先定义状态矩阵,dp[m][n],其中m为word1的长度+1,n为word2的长度+1,为什么+1?因为要考虑如果word1或word2为空的情况,后面可以看到。
定义dp[i][j]为word1中前ii个字符组成的串,与word2中前jj个字符组成的串的编辑距离。
插入操作:在word1的前ii个字符后插入一个字符,使得插入的字符等于新加入的word2[j]。这里要考虑清楚,插入操作对于原word1字符来说,ii是没有前进的,而对于word2来说是前进了一位然后两个字符串才相等的。所以此时是dp[i][j]=dp[i][j-1]+1。
删除操作:在word1的第i−1i−1个字符后删除一个字符,使得删除后的字符串word[:i-1]与word2[:j]相同。这里要考虑清楚,删除操作对于原word2字符来说,j−1j−1是没有前进的,而对于word1来说是删除了一位然后两个字符串才相等的。所以此时是dp[i][j]=dp[i-1][j]+(0 or 1)。
class Solution:
def minDistance(self, word1, word2):
m=len(word1)+1; n=len(word2)+1
dp = [[0 for i in range(n)] for j in range(m)]
for i in range(n):
dp[0][i]=i
for i in range(m):
dp[i][0]=i
for i in range(1,m):
for j in range(1,n):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1
return dp[m-1][n-1]
word1 = "intention"
word2 = "execution"
test = Solution()
print(test.minDistance(word1, word2))





 本文介绍了一个典型的动态规划问题——计算两个字符串之间的编辑距离。通过定义状态矩阵dp[m][n],并详细解释了插入和删除操作如何影响编辑距离的计算。
本文介绍了一个典型的动态规划问题——计算两个字符串之间的编辑距离。通过定义状态矩阵dp[m][n],并详细解释了插入和删除操作如何影响编辑距离的计算。
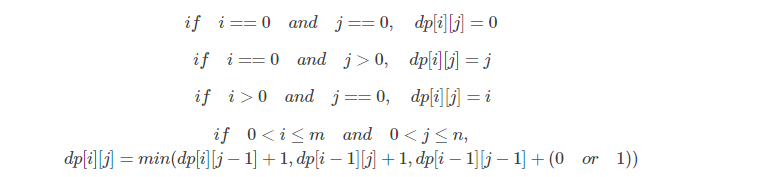
















 2853
2853

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








