数据库查询系统压缩

问题描述

        

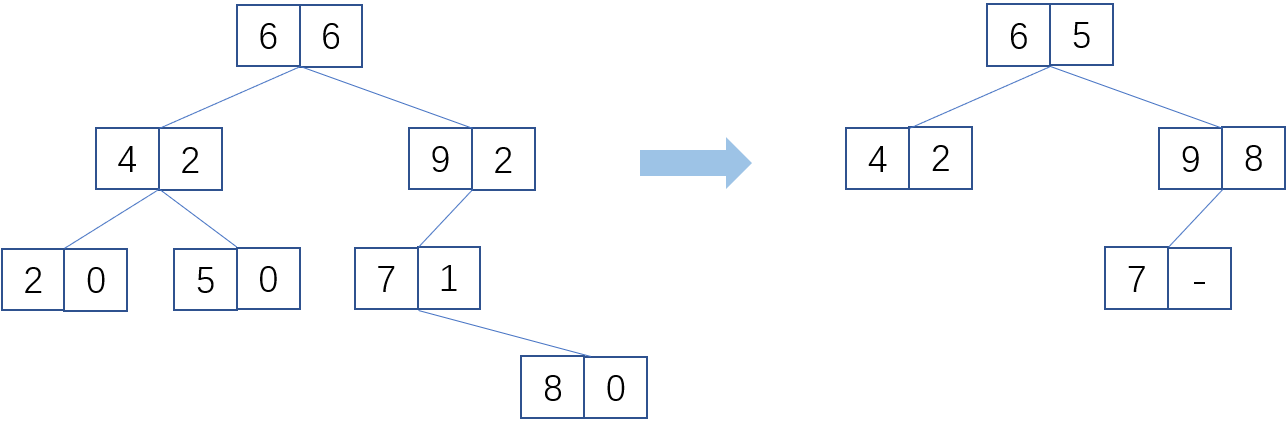
某数据库为提升搜索效率，对某一整型字段构建二叉搜索树(BST)。每个结点包含两个数据信息：1）结点的数据；2）该结点子树的元素数目。为了压缩搜索树规模，该数据库为每个结点增加一个字段，该字段用于存储中序遍历时在访问该结点之前访问的结点数据。在该改进下，被存储的结点如果为叶子结点，该结点在新树中将被删除，以提高存储效率。如果一个叶子结点无中序后继，则无需删除。

给定该BST的先序遍历（第二个字段未给出），请编写程序，输出经过压缩后新BST的先序遍历结果。

输入格式

输入共两行：

第一行为一个int数据n，表示该BST的总结点个数。1<=n<=100000；

第二行为n个int数据，为该BST的先序遍历结果（保证顺序是正确的，并保证数据两两不同）。 每个数据的范围：0<=x<=1*107。

输出格式

输出共一行：

第一行为新BST的先序遍历结果，依序输出结点数据以及保存的其他结点数据（若没有则输出字符-）

输入样例

7
6 4 2 5 9 7 8

输出样例

6 5 4 2 9 8 7 -

提示

1. 需要从先序遍历构建二叉树，并对二叉树进行压缩。

2. 【具体存储规则】题目描述等价于如下表述：对任意结点v：(1) 如果其有左子树，则存储其左子树的最大值，保留该结点；（2）如果没有左子树但有右子树，则不存储任何值，保留该结点；（3）否则（为叶子结点时），如果有中序后继，则可以删除，反之则不存储任何值，保留该结点。

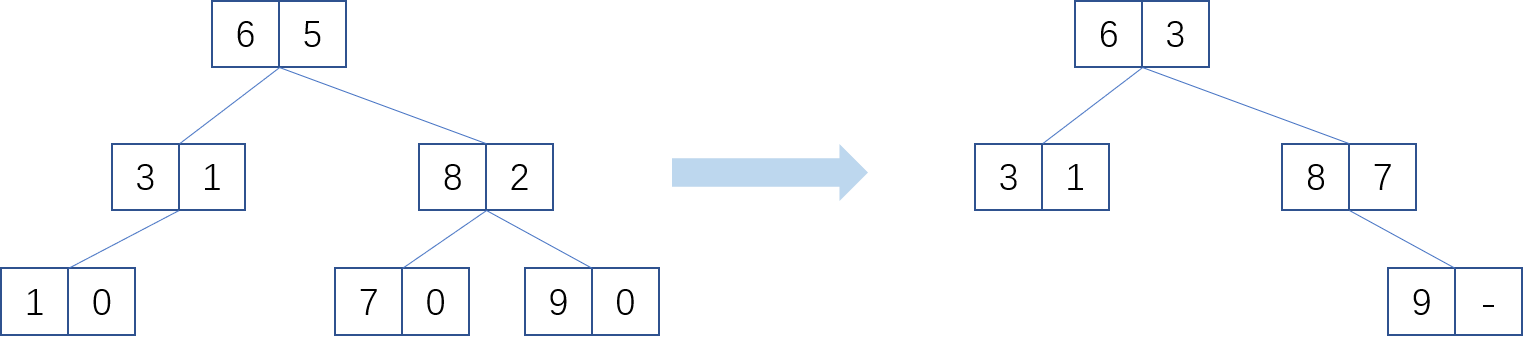
【举例】一些结点可能并未被删除，但你仍需将其记录在中序遍历中下一个结点的第二个字段上（对应规则1）。下面的例子中，尽管左图中结点(3,1)没有被删除，但是为了充分利用已经开辟的存储空间，其父结点仍需存储该节点的值。

3. 注意不要输出多余空格。

4. 个别输入样例需要在压缩二叉树时具有O(1)的空间复杂度，请搜索相关算法实现

问题分析:

       本题有很多坑，比如这句话 "该数据库为每个结点增加一个字段，该字段用于存储中序遍历时在访问该结点之前访问的结点数据。"

        对于以下案例

        最后一个元素的中序前驱应该是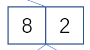，最后理应是

9

8

        直到我看到这句话“（2）如果没有左子树但有右子树，则不存储任何值，保留该结点；（3）否则（为叶子结点时），如果有中序后继，则可以删除，反之则不存储任何值，保留该结点。”

        并且由于题目限制，结构体如果太大无法使用动态申请内存的方式。只能提前以数组的形式申请好内存（原因在于malloc申请的内存会进行内存对齐）

        在构建线索树的同时就找到了节点的中序前驱，时间复杂度会减少很多

以下是AC代码
 

#include<stdio.h>
#include<stdlib.h>
#define MAX_INT  (((unsigned int)(-1))>>1)
typedef struct TNode {
	int val;//结点的值
	//bool valid;布尔型变量valid，为什么不读取但写在这
	struct TNode *left;//结点的左右指针
	struct TNode *right;
	int prev;//新加的字段   本来只用加这个，时间复杂度会降很多，但是奈何不让加啊,一加就超了
}*BTree, TNode;

TNode Nodes[1000000];
int top = 0;

int readNum() { // 快速读入
	char ch = getchar();
	while (ch < '0' or ch > '9') ch = getchar();
	int v = 0;
	while (ch >= '0' and ch <= '9') {
		v = v * 10 + ch - '0';
		ch = getchar();
	}
	return v;
}

BTree createNode(int num) {
//	BTree newNode = (BTree)malloc(sizeof(TNode));
	BTree newNode = Nodes + top++;
	newNode->val = num;
	newNode->prev = -1;
	newNode->left = NULL;
	newNode->right = NULL;
	return newNode;
}

BTree buildBST(int n) {
	BTree root = createNode(readNum());
	BTree cur = root, prev = NULL;
	int num = -1, i = 1, flag = 1;;
	BTree newNode;
	while (1) {
		if (i < n && flag)
			newNode = createNode(num = readNum());
		else if (i == n)
			num = MAX_INT, newNode = NULL;
		flag = 1;
//		if (i == n || (cur->right != NULL && cur->right->val < num))
		if (cur->val > num) { //如果比当前节点小，直接把newnode接在左节点就好
			cur->left = newNode;
			cur->prev = num;
			newNode->right = cur;
			prev = cur;
			//printf("i_%d_步骤1：num=%d__cur.val=%d__cur.prev=%d\n",i, num, cur->val, cur->prev);

			cur = newNode;
			i++;
		} else if (cur->right == NULL || cur->right->val > num) { //如果比cur大，且比cur的parent小。或者到头了
			if (newNode == NULL)break;
			newNode->right = cur->right;
			cur->right = newNode;
			//printf("i_%d_步骤2：num=%d__cur.val=%d__cur.prev=%d\n",i, num, cur->val, cur->prev);

			prev = cur;
			cur = newNode;
			num = -1;
			i++;
		} else {
			BTree tmp = cur->right;
			//printf("i_%d_步骤3：num=%d__cur.val=%d__cur.prev=%d\n",i, num, cur->val, cur->prev);
			tmp->prev = cur->val;
			if (prev->left == cur) {
				prev->left = NULL;
			} else
				prev->right = tmp;
			cur = tmp;
			flag = 0;
		}
		//printf("%d-%d\n",i,cur->val);
	}
	//printf("读入结束\n");
	return root;
}

void preorderMorrisTraversal(BTree root) {
	BTree cur = root;
	while (cur != NULL) {
		if (cur->left != NULL) {
			if (cur->val != -1) {
				printf("%d %d ", cur->val,cur->prev);
				cur->val = -1;
				cur = cur->left;
			} else cur = cur->right;
		} else {
			printf("%d ", cur->val);
			if (cur->prev == -1)
				printf("- ");
			else printf("%d ", cur->prev);
			cur = cur->right;
		}
	}
}



int main() {
	int n;
	scanf("%d", &n);

	BTree root = buildBST(n);

	preorderMorrisTraversal(root);

	return 0;
}