代码随想录Day24 | 回溯

回溯理论

文档讲解：代码随想录
视频讲解： 带你学透回溯算法（理论篇）
状态

回溯就是在递归中回溯。所以回溯函数就是递归函数。
我们在二叉树递归中用到回溯就可以发现使用了回溯的方法，都是需要遍历整个二叉树的。所以使用回溯通常就是暴力搜索解决问题

一般解决问题

1. 组合问题：N个数里面按一定规则找出k个数的集合
2. 切割问题：一个字符串按一定规则有几种切割方式
3. 子集问题：一个N个数的集合里有多少符合条件的子集
4. 排列问题： N个数一定规则全排列，有几种排列方式
5. 棋盘问题： N皇后、解数独
   关于组合和排列： 组合是集合中的元素不强调元素顺序，排列是强调元素顺序

回溯抽象

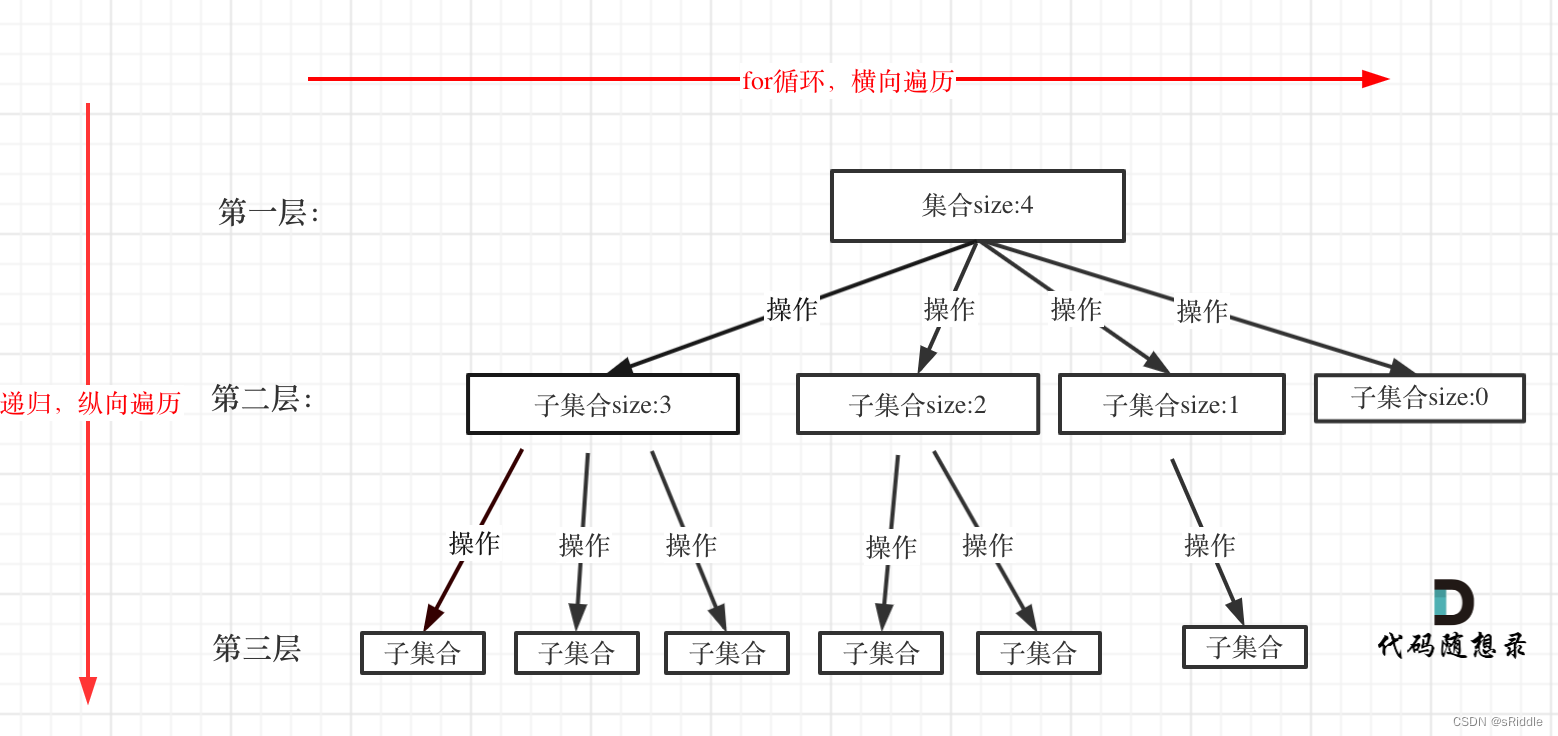
一个回溯问题可以抽象为一棵树，这是由于回溯问题就是在集合中递归查找满足条件的子集，一个集合的大小就构成了树的高度，递归查找的次数可以看作树的深度。

回溯模板

1. 返回值和参数

//一般返回值为void
//参数的确定是需要根据实际逻辑来写的

2. 终止条件
   可以参考我们遍历树的每条路径的道理，回溯的终止条件就是当现在这个结果满足条件时，存放结果然后返回

if(满足条件)
{
	存放
	return ;
}

3. 遍历过程
   

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

这是由于回溯对比二叉树来说，它其实是一个N叉树，所以需要对一层中每个节点进行扫描(for循环)，然后再纵向遍历(递归)

77.组合

文档讲解：代码随想录
视频讲解： 带你学透回溯算法-组合问题（对应力扣题目：77.组合）
状态

注意本题是组合，所以是无序的。
从n个数里面取k个，我们将其对应到上方那个n叉树中，第一层根节点整个集合，第二层就是集合取1个数之后的剩余子集和，并且相对左子树取过的数在第二层集合也不需要出现(避免重复，如果是排列就需要出现了)，那么第三层就是每个父节点再取1个数，直到取满k个数。

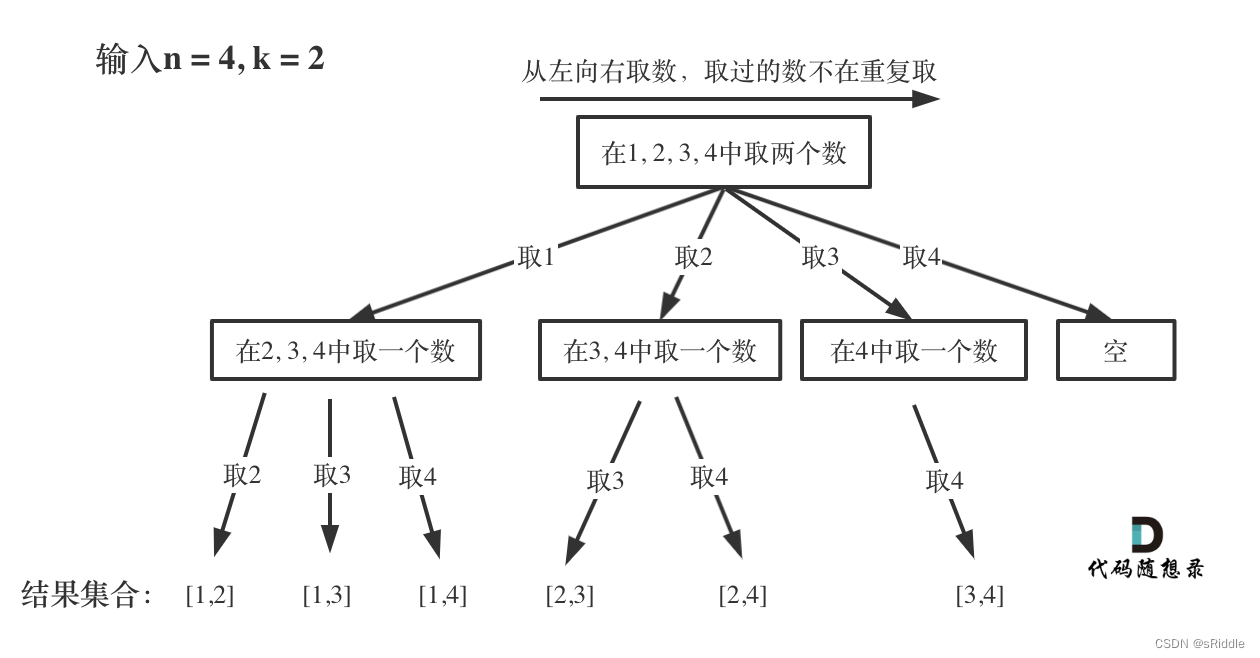
那么终止条件就是当存储数组的长度达到k时，返回并且存储结果。
单层回溯的逻辑就是，对该层的父节点中的每个元素进行递归调用

class Solution {
private:
vector<int> path;
vector<vector<int>> res;

public:
    void backtracking(int n,int k, int targetIndex)
    {
        //终止条件 path的长度 == k
        if(path.size() == k)
        {
            res.push_back(path);
            return ;
        }
        //单层回溯逻辑
        //遍历一层
        for(int i=targetIndex;i<=n;i++)
        {
            //路径压入当前元素
            path.push_back(i);
            //为当前元素的子节点递归
            backtracking(n,k,i+1);
            //弹出压入的元素，回到父节点，开启下一个元素的搜索
            path.pop_back();
        }
        return ;
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n,k,1);
        return res;
    }
};

回溯的优化–剪枝

文档讲解：代码随想录
视频讲解： 带你学透回溯算法-组合问题的剪枝操作（对应力扣题目：77.组合）| 回溯法精讲！
状态

对于这道题目，显然当n-i+1<k-path.size()时就不需要进行递归了，因为之后剩余的元素肯定不存在元素个数=k的数组了。
即如果i>n-(k-path.size())+1之后就不可能在后续子树中找到由k个数组合的数组了

 //修改边界条件到达剪枝
        for(int i=targetIndex;i<=n+1-(k-path.size());i++)
        {
            //路径压入当前元素
            path.push_back(i);
            //为当前元素的子节点递归
            backtracking(n,k,i+1);
            //弹出压入的元素，回到父节点，开启下一个元素的搜索
            path.pop_back();
        }