为什么需要线性代数？

我们说数学是人类用来描绘宇宙秩序和规律的语言，如果说微积分体现了无限细分和无限求和的思想，并揭示了变化和累积的奥秘。那么线性代数就是人类洞察多维世界的强大工具，聚焦于多维空间结构的表示及变换作用。线性代数将数学从单一变量的研究扩展到多维空间的分析，帮助我们处理多维数据、解方程组以及描述复杂的空间关系。

数学的发展始终与人类对世界的探索密切相关，所有的数学刚开始都是为了解决实际问题，而且最初的数学理解起来也不难。只是后来公理化让数学在抽象化的道路上越走越远，使得这套数学体系越来越难理解。线性代数最初为了解决线性方程组求解问题，即如何找到同时满足多个线性方程的未知数。

为了得到线性方程组的解，数学家就想着搞个公式出来，通过公式就能直接得到未知数。看下图就知道这个过程了，方程的解x、y、z都可以通过系数来表示，这是一个通用的求解公式。那么如果扩展到更多维的线性方程组呢？数学家发现方程组的解都可以通过所有系数来表示，而且为了看起来更简洁就抽象成行列式来描述，还定义了很多操作。数学说是为了追求简洁，但也搞出了很多算来算去的运算方式，而且还定义了奇奇怪怪的名字，搞得大家都很懵。

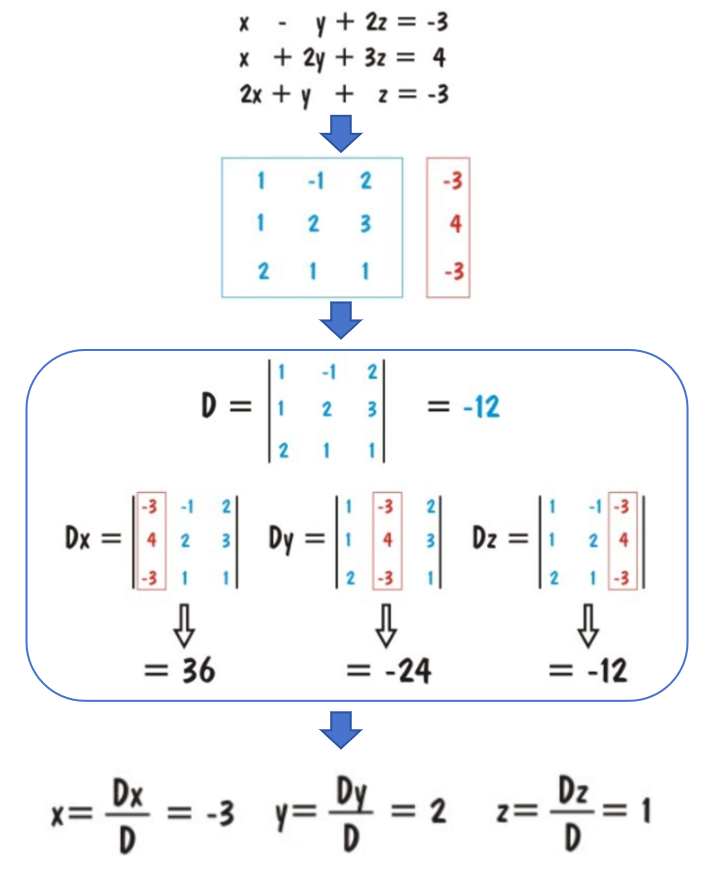
然而行列式其实也不是很方便，而且应用范围有限。于是数学家继续推广到矩阵，这样就能更高效简洁地组织和操作线性方程组，而且还能快速进行各种线性变换。此时不管多少元方程组都可以表示成AX=B矩阵形式，而且通过矩阵运算能很快得到解。也就是说不管多少维都能简洁地表示出来，而且还能做各种运算，在成百上千或更大维度时更难体现出这种优势。

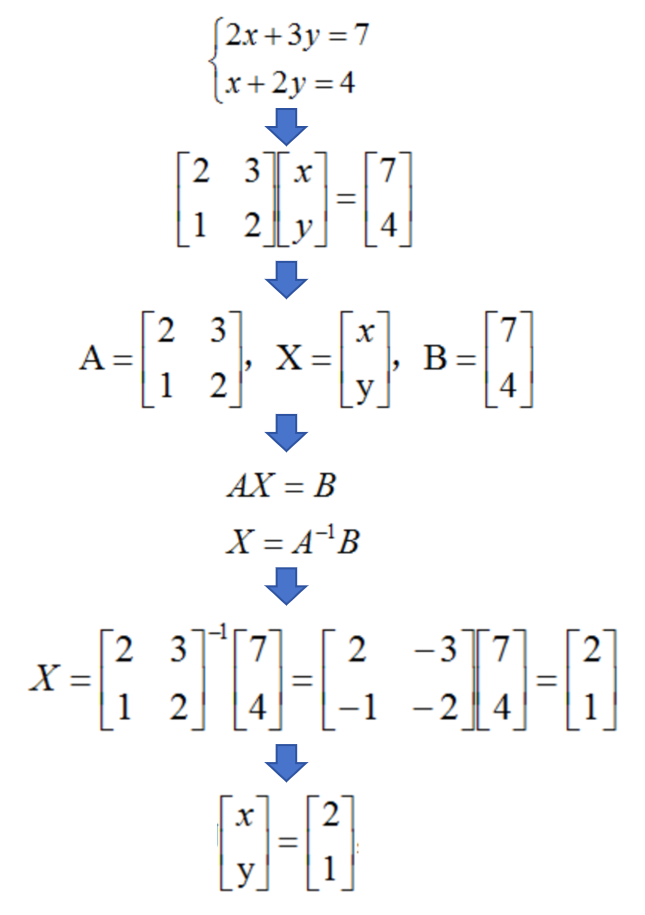
为了完善线性代数分支，提出了向量、矩阵、线性相关、基、向量空间、线性变换、特征向量、内积、正交、奇异值分解等等概念。这些概念都是根据需要定义出来的，都是为了解决向量和矩阵等的线性结构和线性映射变化而提出来，包括线性方程组的解，高维空间的数据表示及几何变换等问题。

线性代数将数学视角从单一维扩展到多维空间，核心就是用来处理多维复杂结构。现在很多学科（物理学、经济学、工程学、统计学等）都涉及到高维结构的处理，举个简单的例子，一张图片其实就是一个矩阵。通过对矩阵的各种操作就能实现相关的图像处理，如果没有矩阵没有线性代数，你能想象如何处理屏幕上百万量级的像素点吗？其实不仅是图片，万物皆可向量化，向量化后才能装进机器里面。

当前人工智能异常火爆，我再讲讲线性代数与人工智能的关系。可以说，没有线性代数就没有当前的人工智能。此轮AI大模型浪潮的核心就是深度学习，而深度学习就是神经网络，神经网络的本质就是层叠的线性变换。训练神经网络就是调整巨大的矩阵参数，使之能得到所定义的最优解。《炉边夜话—深入浅出话AI》有讲AI原理。

神经网络是一种万能函数，理论上通过简单的线性方程嵌套就能拟合任意函数。也就是说不管多复杂的关系，都可以通过线性方程嵌套来逼近。这个世界的规律，也可以通过线性方程来捕获，只要这个方程的参数足够大，它能捕获物理世界的所有运行规律。

线性代数始于线性方程的求解，但又不仅仅限于方程求解。它提供了一套强大而普适的语言和框架，用于描述、分析和处理现实世界无处不在的线性结构和线性变换，展现了高维空间中秩序与结构的美感。一个庞大复杂的系统，蕴藏着由简洁线性规则编织的优雅结构。当我们使用向量和矩阵来编码这个世界时，就必须依赖线性代数。