人工智能的本质是最优化过程

模型三要素

为了将事物和问题转化为最优化问题数学模型我们需要考虑三个要素：因素变量、约束条件和目标函数。我们根据事物和问题先找到影响模型的所有因素变量，然后再根据目的建立一个目标函数用来衡量系统的效果，最后还要找到客观的限制条件并作为模型的约束。

公式

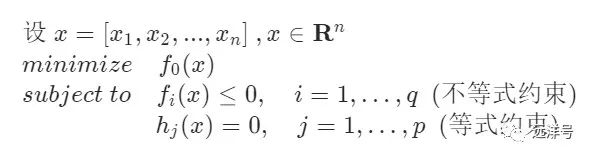
如上公式，实际问题的因素变量其实可以看成是一个n维向量，向量的每个元素都是实数。f0(x)是我们构建的目标函数，我们的目标就是最小化该函数（最大化的情况其实也可以转化为最小化的情况）。fi(x)和hj(x)作为约束函数，分不等式约束和等式约束两类，约束函数用来限制可能空间，如果不存在约束则不需要约束函数。

目标函数

人工智能的最优化

最优化与人工智能有什么关系呢？可以这样说：人工智能在本质上也是一个最优化过程，对于我们要实现的智能，也是通过学习以求得最优解。这是一个总的大框架，人工智能的问题到最后几乎都是回到最优解问题。

不管是传统的机器学习还是大热的深度学习，亦或是大有潜力的强化学习，它们的基础核心思想都可以提升到最优化问题。

最优化

有约束最优化

前面提到过，最优化问题可能存在约束也可能不存在约束，而且有约束的情况比无约束的情况更加复杂。约束又可以分为不等式约束