编译原理（3）：词法分析

        上一篇文章说了词法跟语法以及文法一些概念（看以前的在这里）

        本次来说词法分析的步骤以及用到的工具。

一、语法分析器

        语法分析器就是进行语法分析的工具，是用编程语言编写出的语法分析程序，具有预处理子程序：（剔除无用的空白、跳格、回车和换行等编辑性字符;区分标号区、捻接续行和给出句末符等）、超前搜索识别单词符号、输出单词类别（标识符、运算符、界符等）以及对单词串进行判断的功能。

二、状态转换图

• 状态转换图是一张有限方向图。
• 结点代表状态，用圆圈表示。
• 状态之间用箭弧连结，箭弧上的标记(字符)代表射出结点状态下可能出现的输入字符或字符类。
• 一张转换图只包含有限个状态，其中有一个为初态，至少要有一个终态。

• 一个状态转换图可用于识别(或接受)一定的字符串。

 ps：只简单介绍状态转换图是什么，不介绍它的实现。

三、正规表达式与有限自动机  

      了解几个概念：有穷字母表∑也就是字符集，字符集中的每一个元素称为一个符号，多个符号组成的有穷序列成为字符串。不包含任何符号的字符串称为空字ε，用∑*表示∑上的所有字的全体,包含空字ε。

例如: 设 ∑={a， b}，则 ∑*={ε,a,b,aa,ab,ba,bb,aaa,...}

         ∑*的子集U和V的连接（积）定义为 UV＝{ ab| a∈U & b∈V }   

         V自身的 n次积记为     Vn=VV…V

         规定V的0次积V0={ε}，令    V*=V0∪V1∪V2∪V3∪… 称V*是V的闭包;

         记 V＋＝VV* ，称V+是V的正则闭包。

            闭包与正则闭包在前面的文章讲过，可以去翻一下。

1.正规式与正规集

          正规集可以用正规表达式（简称正规式）表示，正规表达式是表示正规集一种方法，即能用正规式或正规文法表示的集合称为正规集。一个字集合是正规集当且仅当它能用正规式表示。

   对于正规式的递归定义：

         对给定的字母表∑

 （1）ε和空集都是∑上的正规式，它们所表示的正规集为{ε}和空集;

 （2）任何a∈∑ ，a是∑上的正规式，它所表示的正规集为{a} ;

 （3） 假定e1和e2都是∑上的正规式，它们所表示的正规集为L(e1)和L(e2)，则

•          (e1|e2)为正规式，它所表示的正规集为L(e1)∪L(e2)，
•          (e1.e2)为正规式，它所表示的正规集为L(e1)L(e2)，
•          (e1)*为正规式，它所表示的正规集为(L(e1))*， 

       仅由有限次使用上述三种运算而定义的表达式才是∑上的正规式，仅由这些正规式表示的字集才是∑上的正规集。

    下面看两个例子：

   例1 令∑={a,b}，求下面正规式相应的正规集：

• ba*   ：∑上所有以b为首后跟任意多个a的字
• a(a|b)* ：∑上所有以a为首的字
• (a|b)*(aa|bb)(a|b)* ：∑上所有含相继2个a或相继2个b的字

  例2 令∑={A,B，0,1}，求下面正规式相应的正规集：

• (A|B)(A|B|0|1)* ：∑上标识符的全体
• （0|1）(0|1)*  ：  ∑上数的全体

     同学们仔细体会一下正规式与正规集以及字的概念，后续的文法的语言都是由此处演变过来的。

若两个正规式所表示的正规集相同，则称这两个正规式等价。

对正规式，下列等价成立：

• 交换律     ：e1|e2 = e2|e1         
• 结合律     ：e1 |(e2|e3) = (e1|e2)|e3       
• 结合律     ：e1(e2e3) = (e1e2)e3       
• 分配律     ：e1(e2|e3) = e1e2|e1e3      
• 分配律     ：(e2|e3)e1 = e2e1|e3 e1    
• eε = εe = e         
• e1e2 <> e2 e1  

    EG:

L(e1|e2) = L(e1 ) ∪ L(e2) = L(e2 ) ∪ L(e1) = L(e2|e1)

2.确定有限自动机DNF

      对状态转换图进行形式化，则可以下定义： 自动机M是一个五元式M=(S, ∑, f, S0, F),其中：

• 1. S: 有穷状态集
• 2. ∑：输入字母表(有穷)
• 3. f: 状态转换函数，为S×∑→S的单值部分映射，f(s, a)=s’表示：当现行状态为s，输入字符为a时，将状态转换到下一状态s’。我们把s’称为s的一个后继状态。
• 4. S0∈S是唯一的一个初态；
• 5.F⊆S ：终态集(可空)。   

例如：DFA M=({0，1，2，3}，{a，b}，f，0，{3})， 其中：f定义如下：

     f(0, a)=1        f(0, b)=2       f(1, a)=3          f(1, b)=2

    f(2, a)=1        f(2, b)=3        f(3, a)=3         f(3, b)=3

要注意的几个点：

•         确定有限自动机 DFA可以表示为状态转换图。假定DFA M含有m个状态和n个输入字符，那么，这个图含有m个状态结点，每个结点顶多含有n条箭弧射出，且每条箭弧用Σ上的不同的输入字符来作标记。
•        DFA有限自动机 M能够识别的字的全体记为L(M)。
•        可以证明：∑上的字集V⊆∑*是正规集，当且仅当存在∑上的DFA M，使得V＝L(M)。

3.非确定有限自动机NFA

       定义：一个非确定有限自动机(NFA) M是一个五元式M=(S, ∑, f, S0, F)，其中：   

•  1  S: 有穷状态集；   
•  2  ∑ ：输入字母表(有穷)；  
•  3  f: 状态转换函数，为S×∑*→2**s的部分映射(非单值)；   
•  4 S0∈S是非空的初态集；   
•  5 F ⊆S ：终态集(可空)。

 从定义中可看NFA 和DFA的区别：  

•             弧上的标记可以是∑*中的一个字，而不一定是单个字符；  
•             同一个字可能出现在同状态射出的多条弧上。
•             DFA是NFA的特例。

•        定义：对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’等价。
•       自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的。
•       对于每个NFA M存在一个DFA M’，使得 L(M)=L(M’)。亦即DFA与NFA描述能力相同。

4.非确定有限自动机的确定化

        首先，我们由上述可知：对于每个NFA M存在一个DFA M’，使得 L(M)=L(M’)。亦即DFA与NFA描述能力相同。也就是说能够找到一个与非确定有限自动机等价的确定有限自动机使得他们表示的正规集等价。

NFA确定化——采用子集法：

      设I 是的状态集的一个子集，定义I 的 ε-闭包 ε-closure(I)为:  

         i) 若s∈I，则s∈ε-closure(I)；  

         ii) 若s∈I，则从s出发经过任意条ε弧而能到达的任何状态s’都属于ε-closure(I)  

         即   ε-closure(I)=I∪{s’|从某个s∈I出发经过任意条ε弧能到达s’}

  EG：  

     设a是∑中的一个字符，定义 Ia= ε-closure(J)   其中，J为I中的某个状态出发经过一条a弧而到达的状态集合。

     

            ε-closure({1})={1，2}=I  

            J={5，4，3}  

            Ia= ε-closure(J)=ε-closure({5，4，3}) ={5，4，3，6，2，7，8}

确定化的过程

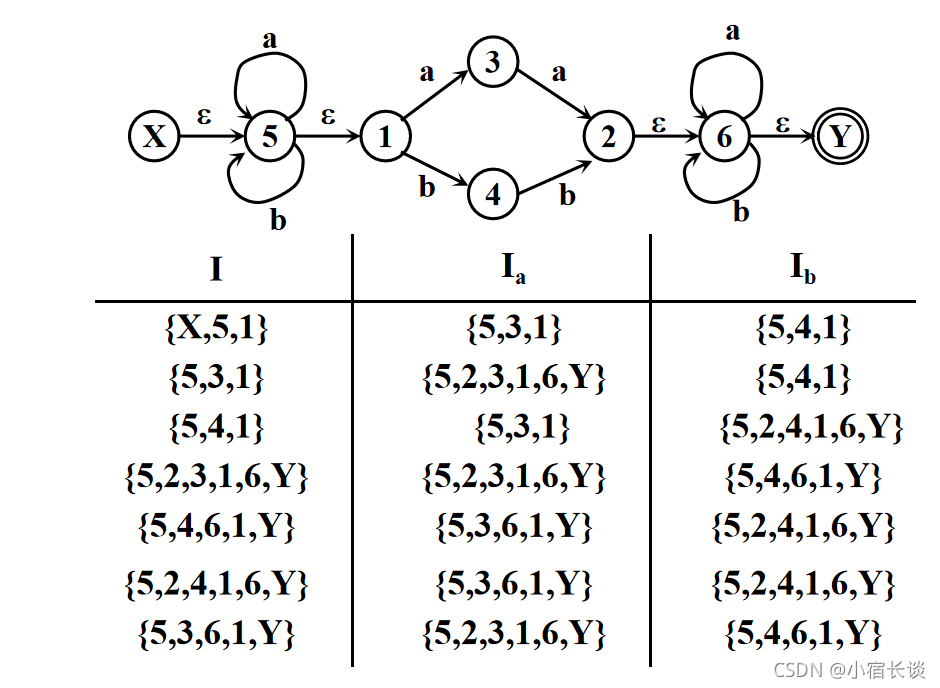
       不失一般性，设字母表只包含两个字符a和b，我们构造一张表:

           

         I ： ε-Closure({X})                          Ia                      Ib-     

                       .......                                 ......                  .......

•        首先，置第1行第1列为 ε-closure({X})求出这一列的Ia，Ib；
•        然后，检查这两个Ia，Ib，看它们是否已在表中的第一列中出现，把未曾出现的填入后面的空行的第1列上，求出每行第2，3列上的集合...
•       重复上述过程，直到所有第2，3列子集全部出现在第一列为止。

EG:

•  现在把这张表看成一个状态转换矩阵，把其中的每个子集看成一个状态。
• 这张表唯一刻划了一个确定的有限自动机M，它的初态是ε-closure({X}) ，它的终态是含有原终态Y的子集。
• 不难看出，这个DFA M与M’等价

写出状态转换矩阵、画出状态转换图后就是下面这样。 

四、正规文法与有限自动机的等价性

定义：  

• 1.对每一个右线性正规文法G或左线性正规文法G，都存在一个有限自动机(FA) M，使得L(M)＝L(G)。
•  2.对每一个FA M，都存在一个右线性正规文法GR和左线性正规文法GL，使得L(M)＝L(GR)＝L(GL)。

五、正规式与有限自动机的等价性

定义：  

• 1. 对任何FA M，都存在一个正规式r，使得L(r)=L(M)。
• 2. 对任何正规式r，都存在一个FA M，使得L(M)=L(r)。
• 对转换图概念拓广，令每条弧可用一个正规式作标记。(对一类输入符号)

六、有限自动机的化简

       对DFA M的化简:寻找一个状态数比M少的DFA M’，使得L(M)=L(M’)

       假设s和t为M的两个状态，称s和t等价:如果从状态s出发能读出某个字a而停止于终态，那么同样，从t出发也能读出a 而停止于终态；反之亦然。 两个状态不等价，则称它们是可区别的。

1.对一个DFA M最少化的基本思想:    

       把M的状态集划分为一些不相交的子集，使得任何两个不同子集的状态是可区别的，而同一子集的任何两个状态是等价的。最后，让每个子集选出一个代表，同时消去其他状态。

2.具体做法: 对M的状态集进行划分

     首先，把S划分为终态和非终态两个子集，形成基本划分Π。 

     假定到某个时候，Π已含m个子集，记为Π={I(1)，I(2)，......，I(m)}，检查Π中的每个子集看是否能进一步划分:  对某个I(i)，令I(i)={s1,s2, ......,sk}，若存在一个输入字符a使得Ia(i) 不会包含在现行Π的某个子集I(j)中，则至少应把I(i)分为两个部分。

EG:

       假定状态s1和s2经a弧分别到达t1和t2，而t1和t2属于现行Π中的两个不同子集，说明有一个字α， t1读出α后到达终态，而t2读出α后不能到达终态，或者反之，那么对于字aα ， s1读出aα 后到达终态，而s2读出aα 不能到达终态，或者反之，所以s1和s2不等价。

          如果s1、s2不等价则将I(i)分成两半，使得一半含有s1 :   I(i1)={s|s∈I(i)且s经a弧到达t,   且t与t1属于现行Π中的同一子集}    另一半含有s2 : I(i2)=I(i)-I(i1)

•           一般地，对某个a和I(i)，若Ia(i) 落入现行Π中 N个不同子集，则应把I(i)划分成N个不相交的组，使得每个组J的Ja都落入的Π同一子集。这样构成新的划分。
•          重复上述过程，直到Π所含子集数不再增长。
•          对于上述最后划分Π 中的每个子集，我们选取每个子集I中的一个状态代表其他状态，则可得到化简后的DFA M’。
•          若I含有原来的初态，则其代表为新的初态，
•          若I含有原来的终态，则其代表为新的终态。

练习

小结

     语法分析部分说完了，语法分析器的写法并没说，这个需要同学们自行查阅资料。总结来说，重点讲了有限自动机以及确定化，这个是非常重要的，有什么不懂的可以留言，发现错误还请指出。谢谢大家观看。