算法—双指针

1.基本介绍

严格的来说，双指针只能说是是算法中的一种技巧。

双指针指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个相同方向（快慢指针）或者相反方向（对撞指针）的指针进行扫描，从而达到相应的目的。最常见的双指针算法有两种：一种是，在一个序列里边，用两个指针维护一段区间；另一种是，在两个序列里边，一个指针指向其中一个序列，另外一个指针指向另外一个序列，来维护某种次序。

双指针算法的核心思想（作用）：优化

在利用双指针算法解题时,考虑原问题如何用暴力算法解出,观察是否可构成单调性,若可以,就可采用双指针算法对暴力算法进行优化

2.例题

1.唯一的雪花

UVA11572 唯一的雪花 Unique Snowflakes - 洛谷

解法：

暴力枚举 -> 枚举出所有符合要求的子数组

两层for循环，可以枚举出所有子数组 ，时间复杂度O(n*n) 超时

如何判断枚举的子数组中，所有元素全都不同？ 借助哈希表 O(1)

先来模拟一下暴力枚举的做法：

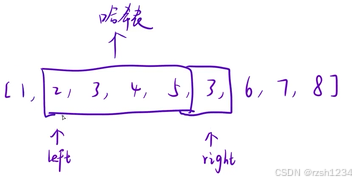
最开始 left ,right 在初始位置1

right向后循环 ，right 向后走一步就借用哈希表判断一下这个元素出现了几次

直到 j 走到图示时，3出现了两次，right 停止循环，left++ ，right 回到 left 位置

 

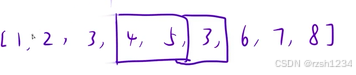
 right 回到 left 位置后，继续向右循环，直到 right 再次走到第二个3位置，借用哈希表判断，3出现两次，right 结束循环 ，同理 left++ , right 又回到 left 的位置

所以我们发现，left 只要在第一个3之前 (或者在3位置)，right 就不会向后移动超过第二个3位置

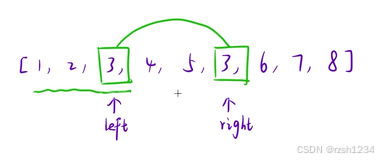
当前(left,right)之间不合法(出现相同数字)时，就没有必要让 right 再往回退，走重复的路程，仅需让left自己往后移动即可

如果left向后移动，直到(left,right)之间位置合法时，也没有必要让right回退到left位置(因为即使right回退到left位置，还是要从left位置向后走到right位置，再往后遍历，不需要走重复路程，直接向后遍历即可)

利用单调性，使用同向双指针来优化

通过枚举暴力解法，发现性质：在暴力枚举过程中，left 以及 right 是可以不回退的

同向双指针相当于滑动窗口，窗口内的值就是符合要求的(每个元素只有一个)

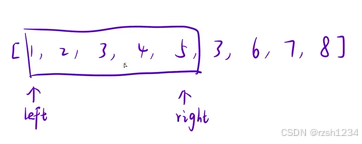
用哈希表维护窗口信息

right向后移动一次，就把right对应的值进入窗口，用哈希表判断当前值出现几次，出现超过一次窗口就不合法

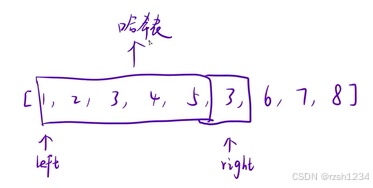
窗口不合法，left++，直到窗口合法 

更新结果：合法窗口内最多的元素

代码：

#include<iostream>
#include<unordered_map>
using namespace std;

int t, n;
const long long N = 1e6+10;
int a[N];


int main()
{
	cin >> t;
	while (t--)
	{
		cin >> n;
		for (int i = 1;i <= n;i++) cin >> a[i];

		int left = 1, right = 1,ret = 0; //初始化
		unordered_map<int, int> mp;
		while (right <= n)
		{
			mp[a[right]]++;  //进窗口
			if (a[right] > 1)  //判断窗口是否合法
			{
				mp[a[left]]--;  //出窗口
				left++;
			}
			right++;
			ret = max(ret, right - left + 1); //更新结果
		}
		cout << ret << endl;
	}

	return 0;
}

2.逛画展

P1638 逛画展 - 洛谷

 解法：

暴力枚举所有符合要求的子数组

如何判断子数组是否包含m种数字 (一个数组mp[ ] + 变量kind)

从前往后遍历的过程中，mp[i] 由0变为1时，说明他之前不存在，现在存在了，让kind++即可

模拟暴力枚举的解法

最开始 i j 在起始位置，j 向后遍历，当子数组中包含了m种数字时，j停止遍历，i++

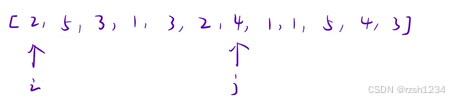
j 回到 i 位置，继续往后遍历，直到找到m种数字 

 

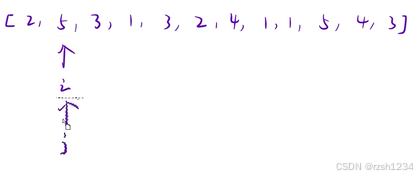
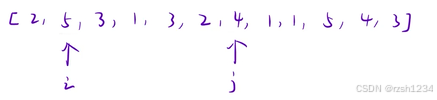
i 从头遍历到尾，找出最小子数组即可

但是暴力枚举时间复杂度为O(n*n)会超时

利用单调性，使用滑动窗口来优化

与暴力枚举类似，先枚举到第一个符合条件的子数组

与暴力枚举不同的是，left++时，right不需要回退 ,因为即使回退也还要再走一遍相同的路线

 

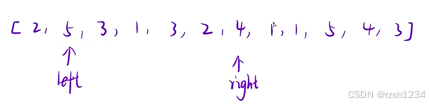
 只需让left++ ，滑动窗口变小，当不符合条件时，right再向后遍历，直到遍历到最后一个数值

代码：

#include<iostream>
using namespace std;

const int N = 1e6 + 10;
int a[N];
int mp[N];//统计窗口内每个元素出现的次数
int n, m,kind;

int main()
{
	cin >> n >> m;
	for (int i = 1;i <= n;i++) cin >> a[i];

	int left = 1, right = 1;
	int ret = n, begin = 1;
	while (right <= n)
	{
		if (mp[a[right]]++ == 0) kind++; // 进窗口

		while(kind == m) // 判断
		{
			int len = right - left + 1;
			if (ret > len)
			{
				ret = len;
				begin = left;
			}

			if (mp[a[left]]-- == 1) kind--;
			left++;
		}

		right++;
	}

	cout << begin << " " << ret + begin - 1 <<endl;
	
	return 0;
}

3.字符串

字符串

代码 

#include<iostream>
#include<string>
#include<unordered_map>
using namespace std;


string s;
int mp[26];
int kind;

int main()
{
    cin >> s;
    int left = 0, right = 0;
    int ret = s.size(); 
    while (right < s.size())
    {
        if (mp[s[right] - 'a']++ == 0)
            kind++;
        while (kind == 26)
        {
            ret = min(ret, right - left + 1);
            if (mp[s[left] - 'a']-- == 1)
                kind--;
            left++;
        }
        right++;
    }
    cout << ret << endl;
    return 0;
}

4.丢手绢

https://ac.nowcoder.com/acm/problem/207040

解法：

针对第 i 个人，如何找出距离他最远的那个人离他的距离是多少？

可能有两个：一个是顺时针的最远，另一个是逆时针的最远

从1号小朋友开始往后枚举，用变量k表示1号小朋友到第 i 号小朋友的距离

sum表示所有小朋友的间距之和

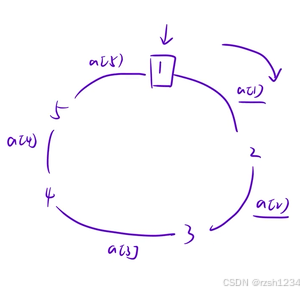
假如加上a [3] 时，第一次出现 k >= (sum)/2，说明1号小朋友顺时针走最远走到3号小朋友，逆时针最远走到4号小朋友

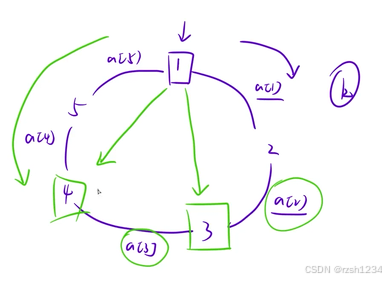
关心第一次出现 2*k >= sum 的位置

暴力枚举：

暴力枚举所有小朋友距离别的小朋友的最远距离

两个变量，两层for循环，left枚举起始位置，right枚举终止位置。当第一次枚举到2*k >= sum 的位置时，枚举终止，求顺时针走的距离和逆时针走的距离，再取最大值

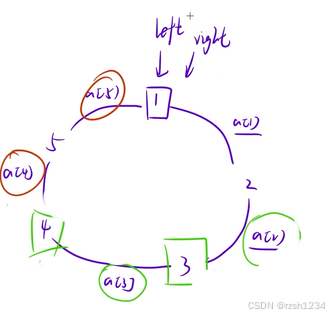
双指针优化

当我们「暴⼒枚举」的过程中，固定⼀个起点位置 left，然后right 之后向后遍历时，记 k为

[left , right]之间的距离。当第⼀次扫描到 k*2 >= sum时，此时我们会发现：

right ⽆需再向后遍历，因为继续向后⾛的结果⼀定不是最优的；

left 向后移动⼀格之后,right指针也不⽤回退，因为我们已经维护出来 区间[ left , right]的 信息,right回退也不是最优解。

代码：

#include<iostream>
using namespace std;

typedef long long LL;
const int N = 1e5+10;
LL a[N];
int n,sum;


int main()
{
    cin>>n;
    for(int i = 1;i <= n;i++)
    {
        cin>>a[i];
        sum += a[i];
    }
    int left = 1,right = 1,k = 0;
    int ret = 0;
    while(right <= n)
    {
        k += a[right]; //进窗口
        while(2*k >= sum) //判断
        {
            ret = max(ret,sum-k); //更新结果
            k -= a[left++]; //出窗口
        }
        ret = max(ret,k); //更新结果
        right++;
    }
    cout<<ret<<endl;
    return 0;
}