聚类1：K-means与k-means++聚类-优快云博客

本文链接：https://blog.youkuaiyun.com/ruoyou521/article/details/132367741

聚类

1、聚类基础
2、K-means聚类（划分式聚类方法）
- 2.1 算法原理
- 2.2 python实现（k-means数据以及代码）
3、K-Means++算法（划分式聚类方法）

1、聚类基础

1.1 定义

(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得**同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。**也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

1.2 聚类和分类的区别

聚类(Clustering)：是指把相似的数据划分到一起，具体划分的时候并不关心这一类的标签，目标就是把相似的数据聚合到一起，聚类是一种无监督学习(Unsupervised Learning)方法。
分类(Classification)：是把不同的数据划分开，其过程是通过训练数据集获得一个分类器，再通过分类器去预测未知数据，分类是一种监督学习(Supervised Learning)方法。

https://blog.youkuaiyun.com/pearl8899/article/details/126457302

1.3 聚类的分类

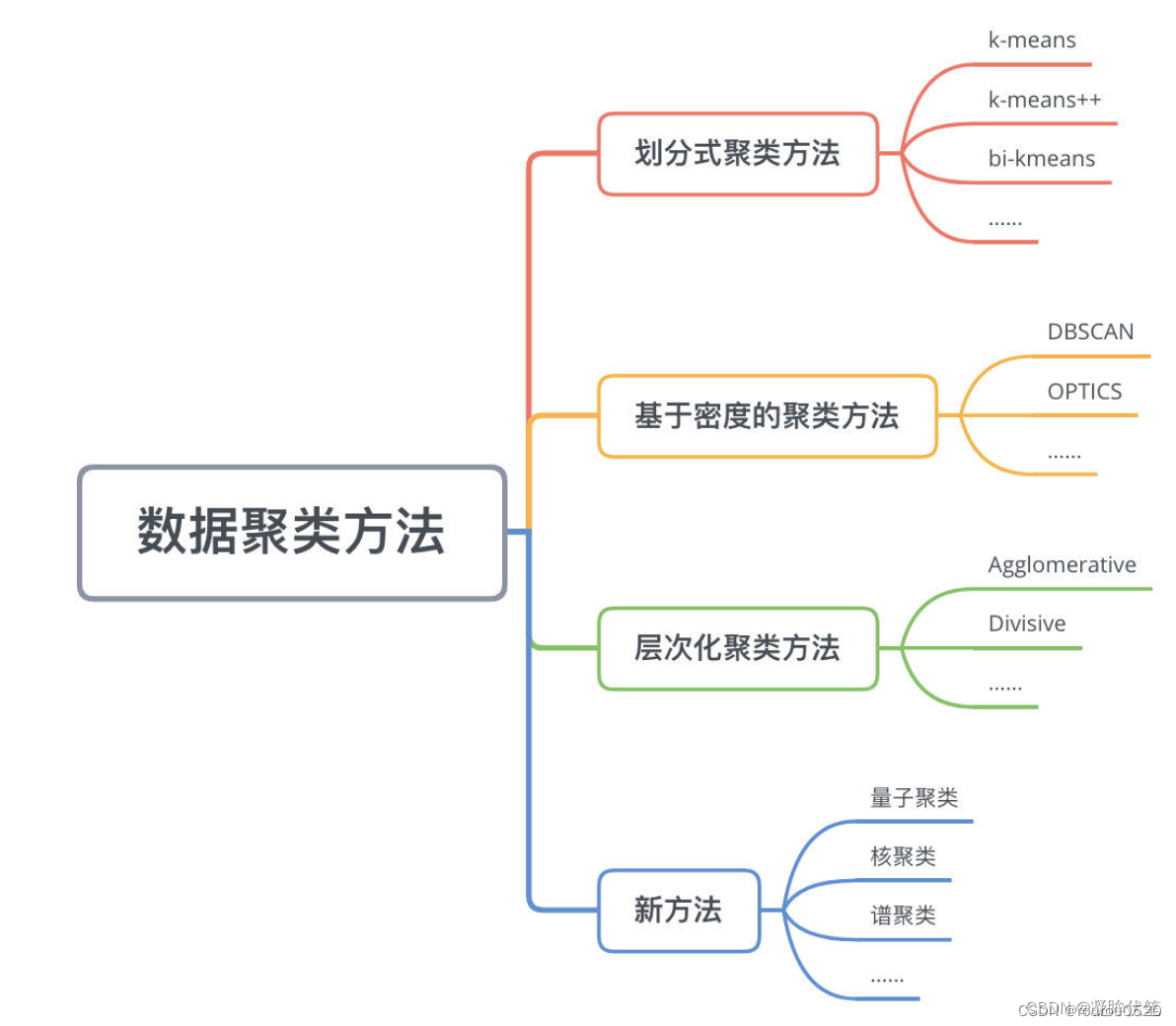
在这里插入图片描述
1、划分式聚类：
划分式聚类方法需要事先指定簇类的数目或者聚类中心，通过反复迭代，直至最后达到"簇内的点足够近，簇间的点足够远"的目标。
它通过将对象划分为互斥的簇进行聚类，每个对象属于且仅属于一个簇；划分结果旨在使簇之间的相似性低，簇内部的相似度高；

2、基于层次的聚类：
层次聚类的应用广泛程度仅次于基于划分的聚类，核心思想是通过对数据集按照层次，把数据划分到不同层的簇，从而形成一个树形的聚类结构。层次聚类算法可以揭示数据的分层结构，在树形结构上不同层次进行划分，可以得到不同粒度的聚类结果。

按照层次聚类的过程分为自底向上的聚合聚类和自顶向下的分裂聚类。聚合聚类以AGNES、BIRCH、ROCK等算法为代表，分裂聚类以DIANA算法为代表。

自底向上的聚合聚类将每个样本看作一个簇，初始状态下簇的数目等于样本的数目，然后然后根据一定的算法规则，例如把簇间距离最小的相似簇合并成越来越大的簇，直到满足算法的终止条件。
自顶向下的分裂聚类先将所有样本看作属于同一个簇，然后逐渐分裂成更小的簇，直到满足算法终止条件为止。
目前大多数是自底向上的聚合聚类，自顶向下的分裂聚类比较少

总结：
基于划分聚类和基于层次聚类的方法在聚类过程中根据距离来划分类簇，因此只能够用于挖掘球状簇

3、基于密度的聚类：
基于密度聚类算法利用密度思想，将样本中的高密度区域(即样本点分布稠密的区域)划分为簇，将簇看作是样本空间中被稀疏区域(噪声)分隔开的稠密区域。
这一算法的主要目的是过滤样本空间中的稀疏区域，获取稠密区域作为簇基于密度的聚类算法是根据密度而不是距离来计算样本相似度，所以基于密度的聚类算法能够用于挖掘任意形状的簇，并且能够有效过滤掉噪声样本对于聚类结果的影响。
https://blog.youkuaiyun.com/weixin_43584807/article/details/105539675

https://blog.youkuaiyun.com/weixin_44177594/article/details/115975110

2、K-means聚类（划分式聚类方法）

2.1 算法原理

,K-means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，即用每一个的类的质心对该簇进行描述。

其算法思想大致为：先从样本集中随机选取 k个样本作为簇中心，并计算所有样本与这 k个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。
根据以上描述，我们大致可以猜测到实现kmeans算法的主要四点：
（1）簇个数 k 的选择
（2）各个样本点到“簇中心”的距离
（3）根据新划分的簇，更新“簇中
（4）重复上述2、3过程，直至"簇中心"没有移动

2.2 python实现（k-means数据以及代码）

sklearn库中的KMeans函数

引用：https://blog.youkuaiyun.com/wyn1564464568/article/details/125782286

函数说明：

KMeans类的初始化参数n_clusters即簇数k kk;
random_state是用于初始化选取k kk个向量的随机数种子;
kmeans.labels_即每个点所属的簇；
kmeans.predict方法预测新的数据属于哪个簇;
kmeans.cluster_centers_返回每个簇的中心。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd


#-------------------------------1.导入数据，聚类只需要数值，不需要属性--------------------------------#
df = pd.read_excel('k-means.xlsx')  # 城市数据
Name = df['城市名称']      #列
X = df.iloc[:, 1:3]   #第而到三列
future_labels = X.columns[0:]   #行（首行）

#-------------------------------2.寻找最佳K值  手肘原则--------------------------------#
## 寻找最佳K值
x1 = df[['生活消费', '学习消费']].values
print(x1)
Name1 = df['城市名称'].values
print(Name1)


'''
inertia = []
for i in range(1, 11):
    km = KMeans(n_clusters=i)
    km.fit(X)
    inertia.append(km.inertia_)  # 簇内的误差平方和
plt.figure(figsize=(12, 6))
plt.plot(range(1, 11), inertia)

plt.title("寻找最佳K值")
plt.xlabel('簇的数量')
plt.ylabel('簇内误差平方和')
plt.show()
##手肘原则
'''



# *======================2. 加载数据，创建K-means算法实例，并进行训练，获得标签====================**
km = KMeans(n_clusters=4, random_state = 0)  # 2.创建实例
label = km.fit_predict(x1)  # 3.调用Kmeans（）fit_predict()方法进行计算，计算簇中心以及标号
expenses = np.sum(km.cluster_centers_, axis=1)    #簇中心每一行向量相加axis=1
# print(expenses)
CityCluster = [[], [], [], []]  #按label分成设定的簇
for i in range(len(Name1)):
        CityCluster[label[i]].append(Name1[i])  # 将每个簇的城市输出
for i in range(len(CityCluster)):  # 将每个簇的平均花费输出
        print("Expenses:%.2f" % expenses[i])
        print(CityCluster[i])

3、K-Means++算法（划分式聚类方法）

K-Means++算法就是对K-Means随机初始化质心的方法的优化。它可以更好地初始化聚类中心，从而提高聚类结果的准确性和稳定性。

优化地方:
在 k-means 中，初始的聚类中心通常是随机选择的，这可能会导致聚类结果不稳定，因为聚类中心的位置可能会影响最终的聚类结果。
k-means++ 算法通过一种启发式的方式选择初始聚类中心，使得它们彼此之间的距离更远，从而提高聚类结果的准确性和稳定性。

3.1 K-means++算法的操作步骤

1.从数据集中随机选择一个数据点作为第一个质心。

2.对于每个数据点x，计算它与已选取的质心中距离最近的距离D(x)，并将D(x)的值累加起来得到一个累积距离S。

3.从剩余的数据点中随机选择一个数据点y，使得每个数据点被选中的概率与它与已选取的质心中距离最近的距离的平方成正比，即P(y) = D(y)^2 / S。这样选择的质心距离已选取的质心较远，从而保证了初始质心的分布更加广泛。

4.重复步骤2和步骤3，直到选取k个质心为止。

5.运行K-means算法，将数据点分配到最近的质心，并更新质心的位置。

6.重复运行步骤5，直到质心的位置不再改变或达到最大迭代次数。

原文链接：https://blog.youkuaiyun.com/qq_40276082/article/details/130237784

3.2 matlab实现

% 生成数据
X = [randn(100,2); randn(100,2)+5; randn(100,2)+10];

%聚类种类
K = 3;
max_iters = 10;
centroids = init_centroids(X, K);

% 迭代更新簇分配和簇质心
for i = 1:max_iters
    % 簇分配
    labels = assign_labels(X, centroids);
    % 更新簇质心
    centroids = update_centroids(X, labels, K);
end

% 绘制聚类结果
colors = ['r', 'g', 'b'];
figure;
hold on;
for i = 1:K
    plot(X(labels == i, 1), X(labels == i, 2), [colors(i) '*']);
    plot(centroids(i, 1), centroids(i, 2), [colors(i) 'o'], 'MarkerSize', 10, 'LineWidth', 3);
end
title('K-means++ ');
legend('类别1', '质心1', '类别 2', '质心 2', '类别 3', '质心 3');
hold off;
% 初始化簇质心函数
function centroids = init_centroids(X, K)
    % 随机选择一个数据点作为第一个质心
    centroids = X(randperm(size(X, 1), 1), :);
    % 选择剩余的质心
    for i = 2:K
        D = pdist2(X, centroids, 'squaredeuclidean');
        D = min(D, [], 2);
        D = D / sum(D);
        centroids(i, :) = X(find(rand < cumsum(D), 1), :);
    end
end

% 簇分配函数
function labels = assign_labels(X, centroids)
    [~, labels] = min(pdist2(X, centroids, 'squaredeuclidean'), [], 2);
end

% 更新簇质心函数
function centroids = update_centroids(X, labels, K)
    centroids = zeros(K, size(X, 2));
    for i = 1:K
        centroids(i, :) = mean(X(labels == i, :), 1);
    end
end

3.3 python实现

结果与k-means聚类差不多一致

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd

#-------------------------------1.导入数据，聚类只需要数值，不需要属性--------------------------------#
df = pd.read_excel('k-means.xlsx')  # 城市数据
Name = df['城市名称']      #列
X = df.iloc[:, 1:3]   #第而到三列
future_labels = X.columns[0:]   #行（首行）


x1 = df[['生活消费', '学习消费']].values
print(x1)
Name1 = df['城市名称'].values
print(Name1)

#-------------------------------2.构建模型，计算簇中心并标号--------------------------------#

model = KMeans(n_clusters=2, init='k-means++')
model.fit(x1)
label = model.predict(x1)
clusters = np.unique(label)
expenses = np.sum(model.cluster_centers_, axis=1)    #簇中心每一行向量相加axis=1
CityCluster = [[], [], [], []]  #按label分成设定的簇
for i in range(len(Name1)):
        CityCluster[label[i]].append(Name1[i])  # 将每个簇的城市输出
for i in range(len(CityCluster)):  # 将每个簇的平均花费输出
        print("Expenses:%.2f" % expenses[i])
        print(CityCluster[i])

#-------------------------------2.绘图--------------------------------#
for cluster in clusters:
    row_ix = np.where(label == cluster)
    plt.scatter(x1[row_ix, 0], x1[row_ix, 1], label=cluster)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(ncol=2)
plt.show()