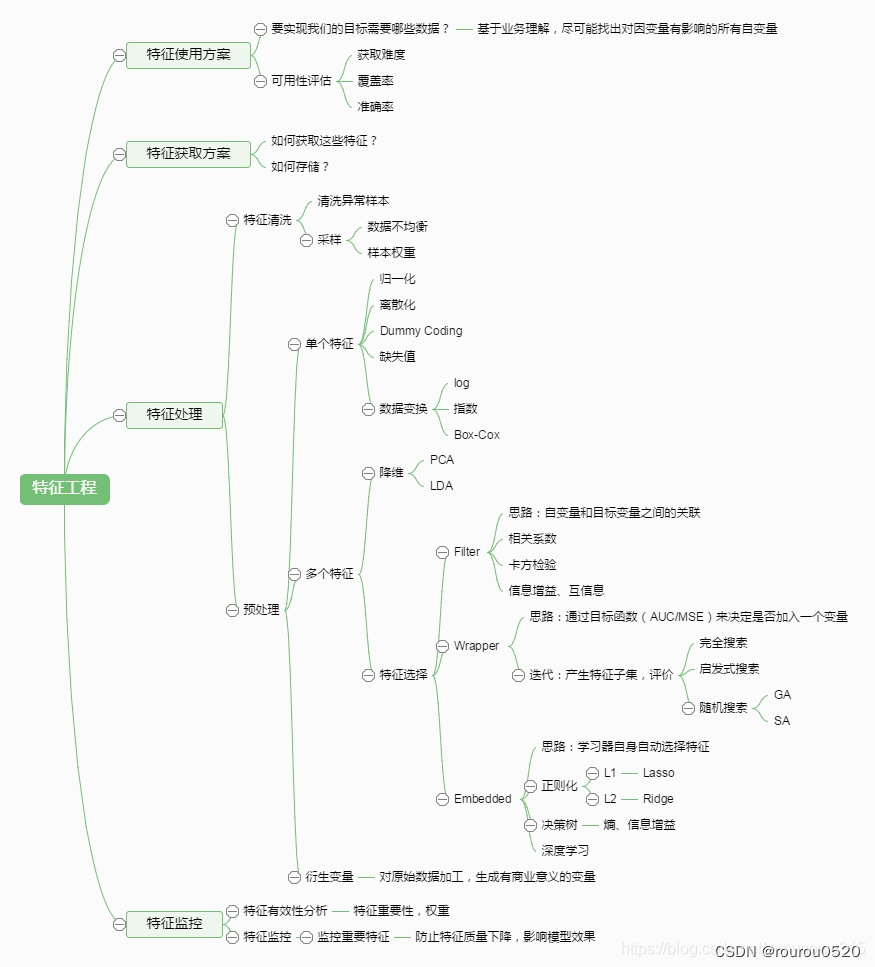
数据降维概述
1、PCA主成分:线性降维
理论参考:
https://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
通过某种线性投影,将高维的数据映射到低维的空间中,并期望方差最大,从而达到使用
较小的数据维度保留较多的原始数据点特征的效果。(PCA的输入数据是不带标签的,所以PCA是一种unsupervised learning)
代码实现
1、https://blog.youkuaiyun.com/weixin_63773176/article/details/132429709?ops_request_misc=&request_id=&biz_id=102&utm_term=python%E5%AE%9E%E7%8E%B0pca%E8%AE%A1%E7%AE%97%E6%9D%83%E9%87%8D&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-5-132429709.142v93chatsearchT3_2&spm=1018.2226.3001.4187
2、https://blog.youkuaiyun.com/ruoff/article/details/116568680
准备
from sklearn.decomposition import PCA #导入主成分分析库
import numpy as np
import pandas as pd
from sklearn import preprocessing
#数据导入
csv_file = "filename.csv"
csv_data = pd.read_csv(csv_file, low_memory=False) # 防止弹出警告
csv_df = pd.DataFrame(csv_data)
#计算相关系数矩阵热力图
sns.heatmap(round(csv_df.corr(), 2),annot=True)
#标准化
scaler = preprocessing.MinMaxScaler().fit(csv_df)
# X = X - X.mean(axis = 0)去中心化
X = pd.DataFrame(scaler.transform(csv_df))
主成分分析建模
pca = PCA(n_components=None) # n_components提取因子数量
# n_components=‘mle’,将自动选取主成分个数n,使得满足所要求的方差百分比
# n_components=None,返回所有主成分
fit = pca.fit(X) #模型训练
print(fit.explained_variance_ ) # 贡献方差,即特征根
print(fit.explained_variance_ratio_) #方差贡献率,各个特征值所占的百分比,也就是每个主成分保留的方差百分比
# 当前保留总方差百分比;总方差百分比越高,说明保留的主成分越多,降维后的数据保留了较多的信息,
print('总方差百分比: ',pca_1.explained_variance_ratio_.sum(),'\n')
print(fit.components_) #得到的主成分,成分矩阵,线性变化规则
#这是PCA类中的属性,表示主成分(特征值)对应的特征向量。特征向量描述了数据的方向,在PCA中,它可以用来了解数据降维过程中的线性变换规则。同时,通过这个属性,也可以了解每个原始特征在新特征构建过程中的权重。
#得到主成分得分
X_train_pca = fit.transform(X_train)
X_test_pca = fit.transform(X_test)
X_train_pca
k1_spss = pca.components_ / np.sqrt(fit.explained_variance_.reshape(-1, 1)) # 成分得分系数矩阵
#可视化
plt.plot(fit.explained_variance_ratio_, 'o-')
plt.xlabel('Principal Component')
plt.ylabel('Proportion of Variance Explained')
plt.title('PVE')
#画累计百分比,判断主成分个数
plt.plot(fit.explained_variance_ratio_.cumsum(), 'o-')
plt.xlabel('Principal Component')
plt.ylabel('Cumulative Proportion of Variance Explained')
plt.axhline(0.9, color='k', linestyle='--', linewidth=1)
plt.title('Cumulative PVE')
#主成分核载矩阵:该矩阵展示了每个主成分是原始数据的线性组合,以及线性的系数
fit.components_
columns = ['PC' + str(i) for i in range(1, 9)]
pca_loadings = pd.DataFrame(fit.components_, columns=csv_df.columns, index=columns)
round(pca_loadings, 2)
#画图展示
# Visualize pca loadings
fig, ax = plt.subplots(2, 2)
plt.subplots_adjust(hspace=1, wspace=0.5)
for i in range(1, 5):
ax = plt.subplot(2, 2, i)
ax.plot(pca_loadings.T['PC' + str(i)], 'o-')
ax.axhline(0, color='k', linestyle='--', linewidth=1)
ax.set_xticks(range(8))
ax.set_xticklabels(csv_df.columns, rotation=30)
ax.set_title('PCA Loadings for PC' + str(i))
确定权重
# 求指标在不同主成分线性组合中的系数
j = 0
Weights = []
for j in range(len(k1_spss)):
for i in range(len(fit.explained_variance_)):
Weights_coefficient = np.sum(100 * (fit.explained_variance_ratio_[i]) * (k1_spss[i][j])) / np.sum(
fit.explained_variance_ratio_)
j = j + 1
Weights.append(np.float(Weights_coefficient))
print('Weights',Weights)
#对权重结果进行归一化
Weights=pd.DataFrame(Weights)
Weights1 = preprocessing.MinMaxScaler().fit(Weights)
Weights2 = Weights1.transform(Weights)
print('Weights2',Weights2)
案例详解:
**> 非常有用:**https://blog.youkuaiyun.com/weixin_46277779/article/details/125533173
2、非线性主成分分析(KPCA:核主成分)

使用近似核心方程处理协方差矩阵,不再进行特征矩阵和特征值的计算(减少计算量),从而直接获得近似的投影后坐标
KPCA, PCA与LDA区别
**1、PCA:**主要用于线性非监督学习(监督学习也可以)的数据降维
**2、LDA:**主要用于线性监督学习的数据降维
**3、KPCA:**得益于PCA非监督及监督学习通吃的特性,KPCA适用于几乎所有的非监督/监督非线性分类问题
理论式:

代码实现:
使用KPCA时最重要的一点就是其内置高斯近似方程参数gamma值,这个值是无法通过理论获得的,只能够通过实践尝试获得较优的gamma值,这里使用的gamma值是15
其中的核函数有多种方法:poly,rfb,cosine
一般rfb多一点
https://blog.youkuaiyun.com/youcans =
https://blog.youkuaiyun.com/WEILING123/article/details/107376184
# Demo of sklearn.decomposition.KernelPCA
from sklearn.datasets import load_iris # Youcans, XUPT
from sklearn.decomposition import KernelPCA, PCA
import matplotlib.pyplot as plt
import numpy as np
X, y = load_iris(return_X_y=True)
print(type(X)) # <class 'numpy.ndarray'>
modelPCA = PCA(n_components=2) # 建立模型,设定保留主成分数 K=2
Xpca = modelPCA.fit_transform(X) # 用数据集 X 训练 模型 modelPCA
modelKpcaP = KernelPCA(n_components=2, kernel='poly') # 建立模型,核函数:多项式
XkpcaP = modelKpcaP.fit_transform(X) # 用数据集 X 训练 模型 modelKPCA
modelKpcaR = KernelPCA(n_components=2, kernel='rbf',gamma=15) # 建立模型,核函数:径向基函数
XkpcaR = modelKpcaR.fit_transform(X) # 用数据集 X 训练 模型 modelKPCA,使用KPCA降低数据维度,直接获得投影后的坐标
modelKpcaS = KernelPCA(n_components=2, kernel='cosine') # 建立模型,核函数:余弦函数
XkpcaS = modelKpcaS.fit_transform(X) # 用数据集 X 训练 模型 modelKPCA,主成分
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
ax4 = fig.add_subplot(2,2,4)
for label in np.unique(y):
position = y == label
ax1.scatter(Xpca[position, 0], Xpca[position, 1], label='target=%d' % label)
ax1.set_title('PCA')
ax2.scatter(XkpcaP[position, 0], XkpcaP[position, 1], label='target=%d' % label)
ax2.set_title('kernel= Poly')
ax3.scatter(XkpcaR[position, 0], XkpcaR[position, 1], label='target=%d' % label)
ax3.set_title('kernel= Rbf')
ax4.scatter(XkpcaS[position, 0], XkpcaS[position, 1], label='target=%d' % label)
ax4.set_title('kernel= Cosine')
plt.suptitle("KernalPCA (Youcans,XUPT)")
plt.show()
自己编写代码:
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
sq_dists = pdist(X, 'sqeuclidean')
mat_sq_dists = squareform(sq_dists)
K = exp(-gamma * mat_sq_dists)
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
alphas = np.column_stack([eigvecs[:, i] for i in range(n_components)])
lambdas = [eigvals[i] for i in range(n_components)]
return alphas, lambdas
- alphas: 直接降维后获得的投影坐标,即是使用sklearn实现时的X_skernpca
- lambdas: 用于对新数据进行投影时的特征向量。我们知道KPCA与PCA最大的一个不同就是获得的矩阵即为投影后的坐标值而不是用于投影坐标转换的特征矩阵,无法对新的训练集数据进行转换处理,lambdas填补了这一缺陷
3、线性判别分析法(LDA)
理论参考:
https://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近(监督学习算法)。
1 from sklearn.lda import LDA
2
3 #线性判别分析法,返回降维后的数据
4 #参数n_components为降维后的维数
5 LDA(n_components=2).fit_transform(iris.data, iris.target)























 916
916

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








