Codeforces Round #695 (Div. 2) C. Three Bags

最新推荐文章于 2026-01-07 18:44:27 发布

原创最新推荐文章于 2026-01-07 18:44:27 发布 · 351 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

博客介绍了Codeforces Round #695 (Div. 2) C题目的解决方案，涉及如何通过特定的移动规则使得三个数集中只剩下一个数，且这个数是所有可能性中的最大值。移动规则包括从两个非空数集中各取一个数，然后将一个数替换为两数之差。博客讨论了如何找到最佳配置以最大化最后剩下的数，涉及到对数列的操作和策略分析。

题目出处:Codeforces Round #695 (Div. 2)
https

题目描绘

C. Three Bags

You are given three bags. Each bag contains a non-empty multiset of numbers. You can perform a number of operations on these bags. In one operation, you can choose any two non-empty bags, and choose one number from each of the bags. Let’s say that you choose number a from the first bag and number b from the second bag. Then, you remove b from the second bag and replace a with a−b in the first bag. Note that if there are multiple occurrences of these numbers, then you shall only remove/replace exactly one occurrence.

You have to perform these operations in such a way that you have exactly one number remaining in exactly one of the bags (the other two bags being empty). It can be shown that you can always apply these operations to receive such a configuration in the end. Among all these configurations, find the one which has the maximum number left in the end.

Input:

The first line of the input contains three space-separated integers n1, n2 and n3 (1≤n1,n2,n3≤3⋅105, 1≤n1+n2+n3≤3⋅105) — the number of numbers in the three bags.
The i-th of the next three lines contain ni space-separated integers ai,1, ai,2, …, ai,ni (1≤ai,j≤109) — the numbers in the i-th bag.

Output:

Print a single integer — the maximum number which you can achieve in the end.

题目解释

题意：

给三个数组，通过一定的规则对三个数组中的元素进行移动，最后剩下一个数时，对该数进行输出，该数应尽可能最大。

移动规则：

数组A,B,C ,可以选数组A中的a元素，B数组中的b元素，然后对A 数组中的a换成a-b，B数组中的b元素移除。

输出：

利用移动规则使三数组剩下最后一个元素，并使该元素为所有情况中的最大值。

思路

该移动规则意味着对某一元素的移动会使其符合发生改变，又因为A,B,C元素均为正，那么移动数为奇数时该元素为负，为偶数则为正。
也就是说当所有元素移动到最后一个元素身上时，保证损失最少并且增量最多即可。

$\left\{ \begin{aligned} A=\{a_1,a_2,...,a_n\}\\ B=\{b_1,b_2,...,b_n\}\\ C=\{c_1,c_2,...,c_n\} \end{aligned} \right.$

设 $A^*,B^*,C^*$ 为 $A, B, C$ 数组除去 $a_1,b_1,c_1$ 的三个数组。

通过移动的规律可以发现答案可能出现在这两种情况下，

$ans=c_1-A+B+C^*$
$ans=c_1-a_1-b_1+A^*+B^*+C^*$

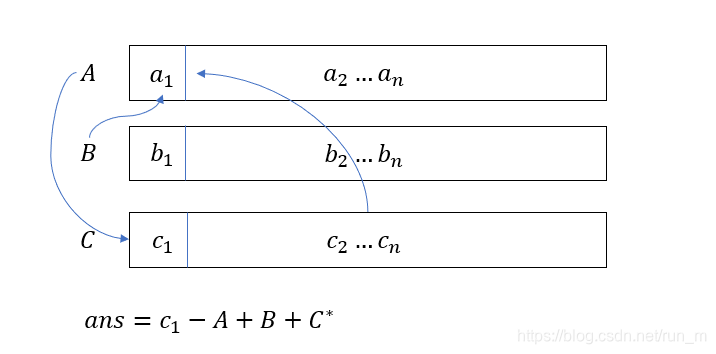
在这里插入图片描述

$B->a_1, A^*->c_1,a_1->c_1$
把整个B的数组所有元素均移动到 $a_1$ 上，即 $a_1-B$ ,消去数组 $B$
再把 $A^*$ 移动到 $c_1$ 上，即 $c_1-A^*$
最后把 $a_1$ 移动到 $c_1$ 上，即 $c_1-a_1$
也就是 $c_1-A$
有因为操作次数的原因，总体对数组A的操作为奇数，B，C则为偶数，故只需要找出最小数组A即可。
$A^*->b_1,B^*->a,a_1->c_1,b_1->c_1$
同上述原理一样，这种情况则 $a_1,b_1$ 为负， $A^*,B^*,C$ 为正
即找出最小的 $a_1,b_1$ 。
因为一个元素的移动是从元素数组删除，再对目标元素进行相减，也就是损失该元素的两倍。

代码实现

可以先对数组A,B,C排序，找到最小的值，即为上述的a1，b1，c1，
因为上述情况中只有A或者a1，b1为需要减去的数值，所以只要事先求和总数然后减去它们。最后对每种答案进行比较即可。

最后上代码：

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
ll a[300000],b[300000],c[300000];
bool cmp(ll x,ll y)
{
    return x<y;
}
int main()
{
    int x,y,z;
    ll ans=0,res;
    ll sum_a=0,sum_b=0,sum_c=0;
    cin>>x>>y>>z;
    for(int i=0;i<x;++i) 
    {
        cin>>a[i];       //存储数组A
        ans+=a[i];       //求三数组的总和
        sum_a+=a[i];     //求数组A的和
    }

    for(int i=0;i<y;++i)  //与A同理
    {
        cin>>b[i];
        ans+=b[i];
        sum_b+=b[i];
    }

    for(int i=0;i<z;++i)  //与A同理
    {
        cin>>c[i];
        ans+=c[i];
        sum_c+=c[i];
    }

    sort(a,a+x,cmp);     //对各数组进行排序，方便找出各数组最小的值
    sort(b,b+y,cmp);
    sort(c,c+z,cmp);

    res=max(max(ans-2*(a[0]+b[0]),ans-2*(a[0]+c[0])),ans-2*(b[0]+c[0]));  //枚举所有可能情况
    res=max(max(max(res,ans-2*sum_a),ans-2*sum_b),ans-2*sum_c);           

    cout<<res;      //输出答案

}