算法编程题-区间子数组个数

摘要：本文将对LeetCode原题 区间子数组个数进行介绍，首先给出自己的实现思路和代码，然后进一步优化过的代码和其他的一些思路，所有代码基于golang语言实现，且通过LeetCode所有测试用例，最后本文将给出各个方法的复杂度分析。
关键词：Golang、LeetCode、双指针、算法

原题描述

LeetCode 795 区间子数组个数：给定一个数组nums，以及下限left和上限right，求所有满足区间最大值在[left, right]范围内的子数组个数。比如，对于nums=[2,9,2,5,6]，left=2，right=8，符合条件的子数组个数为7。

方法一、一次遍历

思路简述

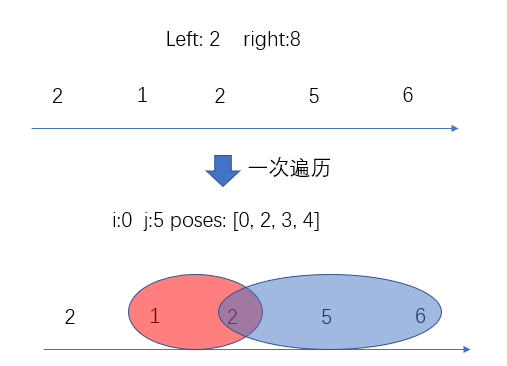
这道题目笔者想了很多种错误的思路包括什么单调栈单调队列堆等等，最后才用双指针梳理出了一种思路和实现。在遍历的过程中，维护右指针j往右移动，直到遇到一个数大于上限right，并且在这一个过程中，维护所有大于等于下限left的数到poses数组中。然后开始计数，枚举上一步得到的所有poses里的数作为某个区间的第一个符合条件的数，显然这样的子数组区间是满足要求的，在下图所示的数据环境中，一次遍历完成后，得到的poses数组为[0，2，3，4]，枚举到以2位置的数2作为第一个符合条件的数的区间时，红色部分是这个区间可能的起点位置，蓝色部分是该区间可能的终点位置，所以这样的区间一共有$2\ast 3=6$个。

但这个过程还是稍微复杂了一点，还有一种简化思路，通过枚举区间的右端点，记录此时符合条件的数最后一次出现的位置为$las{t}_i$，若不存在，则该值为-1，以及最后一次出现的大于上限right的位置为$las{t}_j$，则以当前点为右端点的区间个数为$las{t}_i-las{t}_j$，表示可能的左端点的可能点数目。

代码实现

第一版代码如下：

func numSubarrayBoundedMax(nums []int, left int, right int) int {
	n := len(nums)
	i := 0
	j := 0
	res := 0
	for i < n {
		j = i
		poses := make([]int, 0)
		for j < n && nums[j] <= right {
			if nums[j] >= left {
				poses = append(poses, j)
			}
			j++
		}
		// 计数
		for _, pos := range poses {   // 枚举所有可能结束位置
			res += (pos - i + 1) * (j - pos)
			i = pos + 1
		}
		i = j + 1
	}
	return res
}

LeetCode运行截图如下：

第二版代码如下:

func numSubarrayBoundedMax(nums []int, left int, right int) int {
	n := len(nums)
	i := 0
	lasti := -1
	lastj := -1
	res := 0
	for i < n {
		if nums[i] >= left && nums[i] <= right {
			lasti = i
		}
		if nums[i] > right {
			lastj = i
		}
		res += max(0, lasti - lastj)
		i++
	}
	return res
}

运行截图如下：

复杂度分析

• 时间复杂度：$O(n)$，以第一种方法来说明，看起来有两层循环，但是两层循环里的操作就是访问数组中的一个点，而可以保证数组中的每一个位置至多被访问两次
• 空间复杂度：$O(1)$，第一版在部分数据情况下为$O(n)$

方法二、计数

思路简述

还有一种思路，基于转换思维，区间最大数小于等于right的区间里，既有那些区间最大数介于[left，right]之间的，也有那些区间最大数小于left的，所以可以将这一个问题转换为区间最大数小于等于right的个数减去区间最大数小于等于left-1的个数，即可得符合条件的区间个数。

代码实现

func numSubarrayBoundedMax(nums []int, left int, right int) int {
	return numSubArrLE(nums, right) - numSubArrLE(nums, left - 1)
}

func numSubArrLE(nums []int, target int) int {
	n := len(nums)
	res := 0
	i := 0
	j := 0
	for i < n {
		j = i
		for j < n && nums[j] <= target {
			j++
		}
		res += (j - i + 1) * (j - i) / 2
		i = j + 1
	}
	return res
}

运行截图如下：

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：$O(1)$

参考

• 区间子数组个数