Binary Tree 非递归遍历模板小结(经典!)

置顶 已于 2023-11-01 06:43:40 修改
阅读量1.3k 收藏 5
点赞数
CC 4.0 BY-SA版权
分类专栏： algorithm-design 文章标签： Algorithm 1024程序员节
于 2018-05-28 15:55:56 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/roufoo/article/details/80474819
本文详细介绍了二叉树的前序、中序、后序及层级遍历方法，包括递归与非递归实现，并提供了简洁易懂的代码模板。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

Binary Tree的遍历可分为preorder, inorder, postorder和in-level order四种。前3种可用递归或非递归(基于stack，后进先出)，第4种通常用BFS，基于queue(先进先出)，也可以用DFS，基于stack。注意这里是Binary Tree，不需要是Binary Search Tree。

preorder遍历非递归模板：
遍历顺序为根、左、右
思路：

  1. 如果根节点非空，将根节点加入到栈中。
  2. 如果栈不空，弹出栈顶节点，将其值加加入到数组中。
    2.1 如果该节点的右子树不为空，将右子节点加入栈中。
    2.2 如果左子节点不为空，将左子节点加入栈中。
  3. 重复第二步，直到栈空。
    代码如下：//最终参考版
/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 */

class Solution {
public:
    /**
     * @param root: A Tree
     * @return: Preorder in ArrayList which contains node values.
     */
    vector<int> preorderTraversal(TreeNode * root) {
        if (!root) return {};
        vector<int> result;
        stack<TreeNode*> s;
        s.push(root);
        while(!s.empty()) {
            TreeNode* temp = s.top();
            s.pop();
            result.push_back(temp->val);

            if (temp->right) s.push(temp->right);
            if (temp->left) s.push(temp->left);
        }  
        return result;
    }
};

in-order非递归模板：（非常重要!!!）
遍历顺序为左、根、右

思路
1. 从根节点开始，开始把左节点挨个压栈，直至最左端的叶节点。
2. 若stack不为空，对node=stack.top()，存入结果。
若node无右节点，则pop，并看node在stack前一个位置(也就是新的stack.top)是不是node的父节点，并且node是它的右节点）；若是，也将其pop()。
//注意：根据in-order的特点，如果某个节点无右节点，或者右节点已经访问过，说明这就是根了，应该pop。
若node有右节点，则将其压栈，并将其左节点挨个压栈，直至其左子树的最左端的叶节点。
//注意：根据in-order的特点，如果某个节点还有右节点没访问，那就要先访问右节点，即要先将其压栈。
3. 重复2，直到stack空。

举例如下：
第一个while循环沿着左节点压栈，s={6,5,3,2}, 2是栈顶。
第二个while循环
先将node=s.top()的存入结果(2)，然后看node是否有右节点，这里没有，所以pop()。
然后新的node=s.top()存入结果(3)，这里因为3有右节点4（这里3不能pop，否则4返回就找不到3了），所以将节点4压栈，s={6,5,3,4}。
然后新的node=s.top()存入结果(4)，这里4没有右节点，所以4 pop，然后我们看到4是3的右节点，所以3 pop。然后后面的循环会处理5,6,…。
第三个while循环本质上和第一个while循环一样。
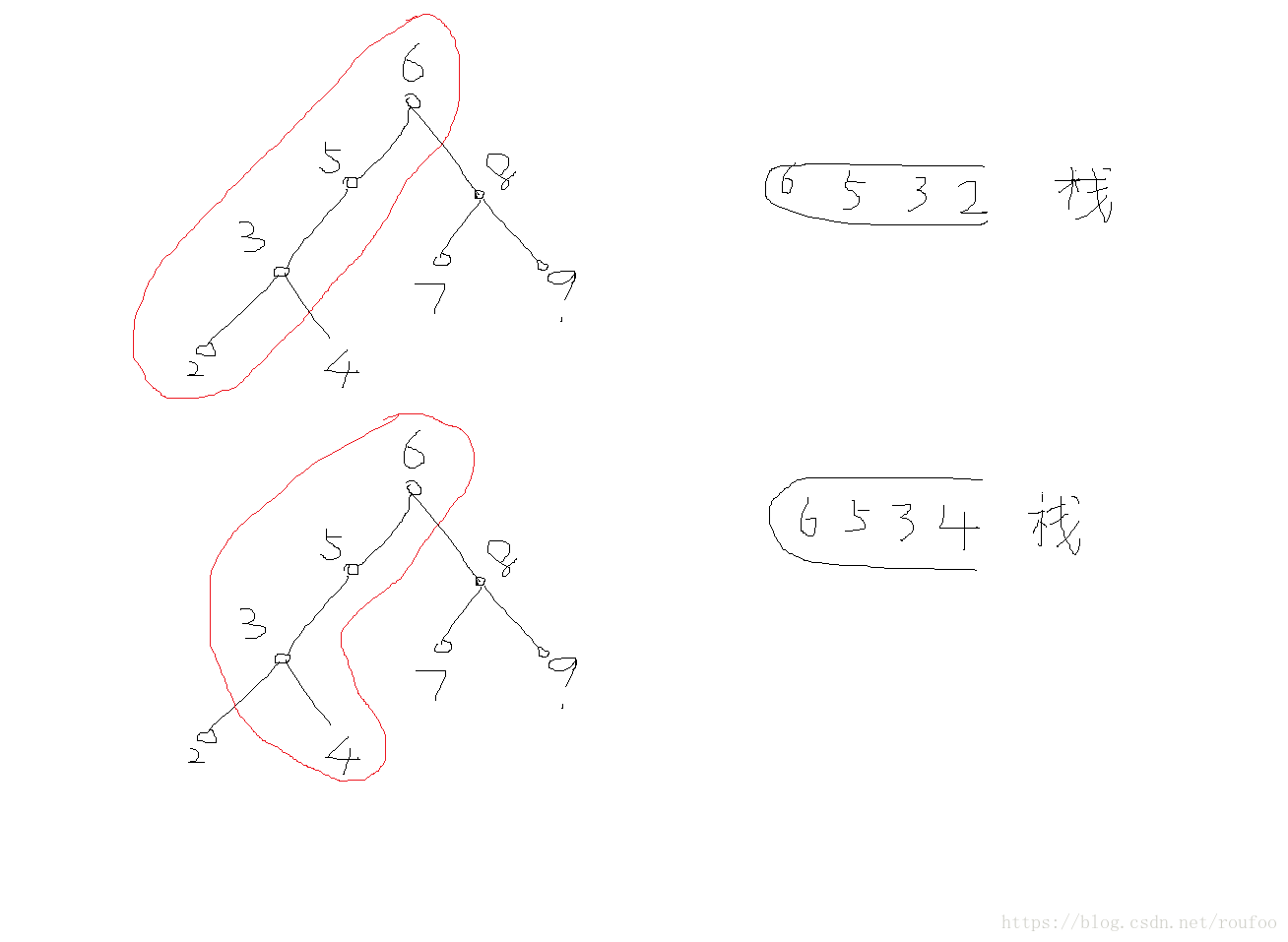
这里写图片描述

代码如下(参考自九章)：//最终参考版
首先访问左子树，将左子树存入栈中，每次将栈顶元素存入结果，如果右子树为空，取出栈顶元素，如果当前元素为栈顶元素右子树，一直弹出至当前元素不为栈顶元素右子树(此处说明访问右子树，根节点已经被访问过，弹出即可)。如果节点右子树不为空，访问右子树，继续循环遍历左子树，存入栈中。

    vector<int> inorderTraversal(TreeNode * root) {
         
        vector<int> result;
        stack<TreeNode *> s;
        if (!root) return result;

        while(root) {
            s.push(root);
            root=root->left;
        }

        while(!s.empty()) {
            TreeNode* node=s.top();
            result.push_back(node->val);
            
            if (!node->right) {
                s.pop();
                while(!s.empty() && (s.top()->right==node)) {
                    node=s.top();
                    s.pop();
                }
            } else {
                node = node->right;
                while(node) {
                    s.push(node);
                    node=node->left;
                }
            }
        }
         
        return result;
    }

又看了一下代码，之前的解释不是很清楚。现在重新解释一下，上面的if(node->right)这个分支好理解，就是如果当前节点有右节点，那就找到右子树的最左边的节点，并沿途挨个压栈。
难点在于if(!node->right)这个分支，为什么有下面这行代码呢? 因为如果没有之前的if(node->right)处理，也就是s.top()没有右子树的话，那就直接s.pop()就可以了，但之前因为s.top()有右节点，进行了if(node->right)的处理，所以s.top()这个节点要推迟到现在才能s.pop()。为啥不能去掉(s.top()->right==node)呢？因为s.top()这个节点和node不一样，node没有右节点，s.top()不一定没有。如果把s.top()不管三七二十一都pop()掉，那么s.top()的右节点就断了，以后也找不到了。

                while(!s.empty() && (s.top()->right==node)) {
                    node=s.top();
                    s.pop();
                }

简化版:
事实上每次stack的top push到res里后就可以从stack里面删掉了，不需要留着。注意下面的这个代码可以用于求二叉树的next iterator，但是不能用于求previous iterator。因为栈里面有些信息已经被删掉了。而上面那个版本不光可以求next iterator,也可以求previous iterator(把代码里面的left 和right互换就可以)。

class Solution {
public:
    /**
     * @param root: A Tree
     * @return: Inorder in ArrayList which contains node values.
     */
    vector<int> inorderTraversal(TreeNode *root) {
        if (!root) return {};
        vector<int> res;
        stack<TreeNode *> stk;

        while (root) {
            stk.push(root);
            root = root->left;
        }

        while (!stk.empty()) {
            TreeNode *node = stk.top();
            res.push_back(node->val);
            stk.pop();
            if (node->right) {
                node = node->right;
                while (node) {
                    stk.push(node);
                    node = node->left;
                }

            }

        }
        return res;
    }
};

post-order非递归模板
遍历顺序为左、右、根

  1. 如果根节点非空，将根节点加入到栈中。
  2. 如果栈不空，取栈顶元素（暂时不弹出），
    i. 如果（左子树已访问过或者左子树为空），且（右子树已访问过或右子树为空），则弹出栈顶节点，将其值加入数组，
    ii. 如果左子树不为空，切未访问过，则将左子节点加入栈中，并标左子树已访问过。
    iii. 如果右子树不为空，切未访问过，则将右子节点加入栈中，并标右子树已访问过。
  3. 重复2，直到栈空。

代码如下：

/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 */

class Solution {
public:
    /**
     * @param root: A Tree
     * @return: Postorder in ArrayList which contains node values.
     */
    vector<int> postorderTraversal(TreeNode * root) {
        vector<int> result;
        stack<TreeNode *> s;
        
        TreeNode * current = root, * lastVisited = NULL;
        
        if (!root) return vector<int>();
        
        s.push(root);
        
        while(!s.empty()) {
            current = s.top();
            if (!lastVisited || current == lastVisited->left || current == lastVisited->right) {
                if (current->left) {
                    s.push(current->left);
                } else if (current->right) { //note! the else is needed here!!!
                    s.push(current->right);
                }
            } else if (current->left == lastVisited) {
                if (current->right) {
                    s.push(current->right);
                }
            } else {
                result.push_back(current->val);
                s.pop();
            }   
            
            lastVisited = current;
        }
        
        return result;
    }
};

下面这个版本更好。//最终参考版
使用栈进行二叉树后序遍历，首先对左子树进行遍历压入栈中，直至左子树为空，然后访问右子树。故每个节点会被访问两次，当节点被第二次访问时，即curr->right=lastvisit时，该节点出栈。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> result;
        stack<TreeNode *> myStack;
        
        TreeNode *current = root, *lastVisited = NULL;
        while (current != NULL || !myStack.empty()) {
            while (current != NULL) {
                myStack.push(current);
                current = current->left;
            }
            current = myStack.top(); 
            if (current->right == NULL || current->right == lastVisited) {
                myStack.pop();
                result.push_back(current->val);
                lastVisited = current;
                current = NULL;
            } else {
                current = current->right;
            }
        }
        return result;
    }
};

上面的几种解法还是没有统一风格，下面是链接
https://www.jianshu.com/p/49c8cfd07410
给出的更统一的模板。非常好。

//更简单的非递归前序遍历
void preorderTraversalNew(TreeNode *root, vector<int> &path)
{
    stack< pair<TreeNode *, bool> > s;
    s.push(make_pair(root, false));
    bool visited;
    while(!s.empty())
    {
        root = s.top().first;
        visited = s.top().second;
        s.pop();
        if(root == NULL)
            continue;
        if(visited)
        {
            path.push_back(root->val);
        }
        else
        {
            s.push(make_pair(root->right, false));
            s.push(make_pair(root->left, false));
            s.push(make_pair(root, true));
        }
    }
}
//更简单的非递归中序遍历
void inorderTraversalNew(TreeNode *root, vector<int> &path)
{
    stack< pair<TreeNode *, bool> > s;
    s.push(make_pair(root, false));
    bool visited;
    while(!s.empty())
    {
        root = s.top().first;
        visited = s.top().second;
        s.pop();
        if(root == NULL)
            continue;
        if(visited)
        {
            path.push_back(root->val);
        }
        else
        {
            s.push(make_pair(root->right, false));
            s.push(make_pair(root, true));
            s.push(make_pair(root->left, false));
        }
    }
}

//更简单的非递归后序遍历
void postorderTraversalNew(TreeNode *root, vector<int> &path)
{
    stack< pair<TreeNode *, bool> > s;
    s.push(make_pair(root, false));
    bool visited;
    while(!s.empty())
    {
        root = s.top().first;
        visited = s.top().second;
        s.pop();
        if(root == NULL)
            continue;
        if(visited)
        {
            path.push_back(root->val);
        }
        else
        {
            s.push(make_pair(root, true));
            s.push(make_pair(root->right, false));
            s.push(make_pair(root->left, false));
        }
    }
}

in-level order 非递归版
思路: 用queue。
一开始将root放入queue中，然后进入while(!queue.empty())，若queue不为空，则按queue中有多少元素(queue.size())，不断取queue.front()，将其值存入结果，再将其左右节点push进queue。周而往复，直到queue空。
代码如下：

/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 */

class Solution {
public:
    /**
     * @param root: A Tree
     * @return: Level order a list of lists of integer
     */
    vector<vector<int>> levelOrder(TreeNode * root) {
        vector<vector<int> > result;
        if (!root) return result;
        
        queue<TreeNode *> q;
        q.push(root);
        
        while(!q.empty()) {
            vector<int> vec;
            int size=q.size();
            for (int i=0; i<size; ++i) {
                TreeNode* node=q.front();
                q.pop();   
                vec.push_back(node->val);
                if (node->left) 
                    q.push(node->left);
                if (node->right)
                    q.push(node->right);
 
            }
            result.push_back(vec);
        } 
        return result; 
    }
};

另外还有二叉树Zigzag遍历，见
https://blog.youkuaiyun.com/roufoo/article/details/103946959

还有二叉树按vertical order遍历，见
https://blog.youkuaiyun.com/roufoo/article/details/103943335

还有二叉树Morris遍历

再来一个二叉树非递归模板，即直接用一个stack模拟系统调用，context存储系统调用中应该保留的信息。这里采用vector而不是stack做栈是因为希望修改stack.top()。

前序遍历


/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

struct Context {
    TreeNode* node;
    int step;
    Context(TreeNode* _node = NULL, int _step = 0) : node(_node), step(_step) {}
};

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<Context> s;
        s.push_back(Context(root, 0));
        vector<int> res;
        while (!s.empty()) {
            if (s.back().node == NULL) {
                //root为空，直接返回
                s.pop_back();
            } else if (s.back().step == 0) {
                s.back().step = 1;
                res.push_back(s.back().node->val);
                //if (s.back().step == 0) s.pop_back();
            } else if (s.back().step == 1) {
                s.back().step = 2;
                s.push_back(Context(s.back().node->left, 0));
            } else if (s.back().step == 2) {
                s.back().step = 3;
                s.push_back(Context(s.back().node->right, 0));
            } else if (s.back().step == 3) {
                //表示当前栈顶的左右子节点都处理完了，这是为了跟step==0做区分，step==0是当前栈顶还没开始处理左右字节点的情况。
                s.pop_back();
            }
        }
        return res;  
    }
};

中序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

struct Context {
    TreeNode* node;
    int step;
    Context(TreeNode* _node = NULL, int _step = 0) : node(_node), step(_step) {}
};

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
     vector<Context> s;
        s.push_back(Context(root, 0));
        vector<int> res;
        while (!s.empty()) {
            if (s.back().node == NULL) {
                //root为空，直接返回
                s.pop_back();
            } else if (s.back().step == 0) {
                s.back().step = 1;
                s.push_back(Context(s.back().node->left, 0));
                //if (s.back().step == 0) s.pop_back();
            } else if (s.back().step == 1) {
                s.back().step = 2;
                res.push_back(s.back().node->val);
            } else if (s.back().step == 2) {
                s.back().step = 3;
                s.push_back(Context(s.back().node->right, 0));
            } else {
                //表示当前栈顶的左右子节点都处理完了，这是为了跟step==0做区分，step==0是当前栈顶还没开始处理左右字节点的情况。
                s.pop_back();
            }
        }
        return res;      
    }
};

后序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

struct Context {
    TreeNode* node;
    int step;
    Context(TreeNode* _node = NULL, int _step = 0) : node(_node), step(_step) {}
};

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<Context> s;
        s.push_back(Context(root, 0));
        vector<int> res;
        while (!s.empty()) {
            if (s.back().node == NULL) {
                //root为空，直接返回
                s.pop_back();
            } else if (s.back().step == 0) {
                s.back().step = 1;
                s.push_back(Context(s.back().node->left, 0));
            } else if (s.back().step == 1) {
                s.back().step = 2;
                s.push_back(Context(s.back().node->right, 0));
            } else {
                res.push_back(s.back().node->val);
                s.pop_back();
            }
        }
        return res;  
    }
};

注意后序遍历中，根节点最后处理，可以顺便弹栈，所以它不用加step=3的情况。为了便于和前序和中序统一版本，也可以加step=3的情况，结果一样。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

struct Context {
    TreeNode* node;
    int step;
    Context(TreeNode* _node = NULL, int _step = 0) : node(_node), step(_step) {}
};

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<Context> s;
        s.push_back(Context(root, 0));
        vector<int> res;
        while (!s.empty()) {
            if (s.back().node == NULL) {
                //root为空，直接返回
                s.pop_back();
            } else if (s.back().step == 0) {
                s.back().step = 1;
                s.push_back(Context(s.back().node->left, 0));
            } else if (s.back().step == 1) {
                s.back().step = 2;
                s.push_back(Context(s.back().node->right, 0));
            } else if (s.back().step == 2) {
                s.back().step = 3;
                res.push_back(s.back().node->val);
            } else {
                s.pop_back();
            }
        }
        return res;  
    }
};

附加一个最好的中序遍历非递归模板，非常简洁。

class Solution {
public:
    /**
     * @param root: A Tree
     * @return: Inorder in ArrayList which contains node values.
     */
    vector<int> inorderTraversal(TreeNode *root) {
        stack<TreeNode *> stk;
        vector<int> res;
        while (root || !stk.empty()) {
            while (root) {
               stk.push(root);
               root = root->left;
            }
            root = stk.top();
            stk.pop();
            res.push_back(root->val);
            root = root->right;
        }
        return res;
    }
};

/////////
个人新总结：

  1. 前序遍历就是自上向下，后序遍历就是自下而上。
    中序遍历其实用得不多，因为如果分叉数不是2的话就不好用中序。
  2. Quick Sort类似于前序遍历，Merge Sort 类似于后序遍历。

准备采用这个模板了。前中后序遍历都可以用。

前序遍历:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (!root) return {};
        visited = new TreeNode(-1);
        vector<int> res;
        goLeft(root, res);
        while (!stk.empty()) {
            TreeNode *topNode = stk.top();
            
            if ((!topNode->left || topNode->left == visited) && topNode->right != visited) {
                //inorder here
                goLeft(topNode->right, res);
            }

            if (!topNode->right || topNode->right == visited) {

                stk.pop();
                visited = topNode;
            }
        }
        return res;
    }
private:
    void goLeft(TreeNode *root, vector<int> &res) {
        while (root) {
            //preorder here
            res.push_back(root->val);
            stk.push(root);
            root = root->left;
        }
        return;
    }
    stack<TreeNode *> stk;
    TreeNode *visited;
};

中序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode *visited = new TreeNode(-1);  //注意：这里不能用visited = NULL，不然跟后面的topNode->left == visited 或 topNode->right == visited搞混。
        pushLeft(root);
        while (!stk.empty()) {
            TreeNode *topNode = stk.top();
            if ((!topNode->left || topNode->left == visited) && (topNode->right != visited)) {
                //左子树遍历完，右子树还没有遍历。中序代码放这里
                res.push_back(topNode->val);
                pushLeft(topNode->right);
          }
            if (!topNode->right || topNode->right == visited) {
                //左子树和右子树都遍历完了。后序代码放这里
                visited = topNode;
                stk.pop();
            }
        }
        return res;
    }
private:
    stack<TreeNode *> stk;
    void pushLeft(TreeNode *root) {
        while (root) {
        //左子树还没有遍历。前序代码放这里
            stk.push(root);
            root = root->left;
        }
    }
};

后续遍历:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if (!root) return {};
        vector<int> res;
        visited = new TreeNode(-1);
        goLeft(root, res);
        while (!stk.empty()) {
            TreeNode *topNode = stk.top();

            if ((!topNode->left || topNode->left == visited) && topNode->right != visited) {
                //inorder here
                goLeft(topNode->right, res);
            }

            if (!topNode->right || topNode->right == visited) {
                //postorder here
                res.push_back(topNode->val);
                stk.pop();
                visited = topNode;
            }
        }
        return res;
    }
private:
    void goLeft(TreeNode *root, vector<int> &res) { //注意goLeft结束后，root值不变。goLeft的作用仅仅是把一系列left的节点压栈。
        while (root) {
            //preorder here
            stk.push(root);
            root = root->left;
        }
        return;
    }
    TreeNode *visited;
    stack<TreeNode *> stk;
};
Java实现二叉链表构建二叉树，实现相关功能
**My Coding Family**
07-23 1042
ok，以上就是我这期的Bug修复内容啦，如果还想查找更多解决方案，你可以看看我专门收集Bug及提供解决方案的专栏《优快云问答解惑-专业版》，都是实战中碰到的Bug，希望对你有所帮助。到此，咱们下期拜拜。码字不易，如果这篇文章对你有所帮助，帮忙给 bug菌 来个，您的支持就是我坚持写作分享知识点传播技术的最大动力。「猿圈奇妙屋」；
Binary-Tree
qq_41747979的博客
08-30 193
二叉树python实现 非递归实现各种遍历以及根据遍历结果恢复树结构
二叉树 (Binary Tree)的遍历
song_hui_xiang
08-15 1691
树是一种比较重要的数据结构，尤其是二叉树。二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。 二叉树节点定义： #define ElementType char typedef struct Node { ElementType data; str
[Data Structure] 重新实现BinaryTree类模板
ingy
12-28 311
二叉树（binary tree）是有限个元素的集合（允许为空）。当二叉树非空时，其中有一个称为根的元素，余下的元素（如果有的话）被组成 2个二叉树，分别称为左子树和右子树。 和树的主要区别是： 二叉树可以为空，树不能为空。 二叉树中每个元素都恰好有两棵子树（其中一个或两个可能为空）。而树中每个节点有若干子树且没有左右这样的区分。 包含n个节点的二叉树的高度最大为n，最小为log(n+...
二叉树(Binary tree)
最新发布
weixin_73966418的博客
07-04 1136
本文系统介绍了树型结构尤其是二叉树的基本概念、实现方法及其应用。树作为一种非线性数据结构，在计算机科学中有着广泛应用。文章首先阐述了树的基本定义、术语和表示方法，然后重点探讨了二叉树的特性，包括完全二叉树和满二叉树的区别、二叉树的遍历算法（前序、中序、后序、层序）及其Java实现。通过详细的代码示例，展示了二叉树的创建、遍历、节点计数等基本操作。同时，文章也介绍了二叉树的数学性质、存储方式（数组与链式结构）以及在实际问题中的应用。掌握二叉树需要理解递归思想，将复杂问题分解为子问题处理。
Binary Tree(构造）
Dizzy的专栏
10-04 392
Binary Tree Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 795    Accepted Submission(s): 466 Special Judge Problem Description The
二叉树
hello world
10-22 665
二叉树： 是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。 1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。 2）左子树和右子树是有顺序的，次序不能任意颠倒。 3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。 斜树： 所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右...
【启发】94. Binary Tree Inorder Traversal（树的非递归遍历 + 栈模拟递归）
课桌
08-16 716
题目 Given a binary tree, return the inorder traversal of its nodes' values. For example: Given binary tree [1,null,2,3], 1 \ 2 / 3 return [1,3,2]. Note: Recursive solution
[算法系列]递归应用——二叉树（1）：二叉树遍历详解解+LeetCode经典题目+模板总结
lawfree的博客
07-04 2087
本文是递归算法系列文的第7篇，依然沿着递归的脉络，介绍了常常运用递归处理问题的一个典型数据结构——二叉树。分析总结了LeetCode中的相关习题在解法上的思路和模板。 本文内容如下： 树的前、中、后序、层次遍历的递归和非递归写法 LeetCode上树的问题分类（基本遍历、路径、计数、加和、深宽、构造、BST等） 两种遍历为思想的问题（判定、比较结点或子树 以及 路径[ 和 ]、累计） 【小结】在解决树的遍历相关问题时，我们是如何使用基本遍历方法，进行递归设计的？ 由于树的相关问题题目较多，本文介绍第
直击高频编程考点：树相关知识及经典算法题总结
热门推荐
张彦峰的博客
10-27 5万+
树相关知识及编程练习总结：背景知识+树的应用举例（Spring中的应用举例+其他框架中的应用举例+实际开发中的应用举例）+相关编程练习（二叉树遍历：包括前序遍历、中序遍历、后序遍历、层序遍历等+二叉树的最大深度+二叉树的最小深度+对称二叉树+二叉树的最近公共祖先+二叉树的直径+二叉树的路径和+二叉搜索树中的插入操作+二叉搜索树中的删除操作+二叉搜索树中的搜索操作+二叉树的层平均值+二叉树的镜像+二叉树的序列化与反序列化+二叉树的右视图+二叉树的最大宽度+前序遍历和中序遍历构造二叉树+平衡二叉树）
ACM算法模板小汇总
羽歌Yo的博客
06-24 2823
一篇想到哪写到哪 · 不太全面的模板大集锦。
二叉树前序遍历算法详解与实现
这里给出的代码实现是模板类`BinaryTree`的成员函数`PreOrder`，它通过递归的方式来完成前序遍历。" 在二叉树递归的前序遍历算法中，首先访问根节点，然后递归地访问左子树，最后访问右子树。这是通过函数`PreOrder...
BinaryTree
分享技术，享受生活
07-10 766
class BinaryTree { // 定义二叉树的操作类 class Node {  @SuppressWarnings("unchecked")  private Comparable data; // 保存操作的数据内容  private Node left; // 左
Binary Tree
caerun
08-30 174
[code="java"]public class BinaryTree { Node root; public void addNode(int key, String name) { // Create a new Node and initialize it Node newNode = new Node(k...
Binary Tree（二叉树）
baidu_27055141的博客
04-23 527
一、定义：在计算机科学中，二叉树是每个结点最多有两个子树的结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree） （1）结点：一棵的深度为K，且结点为2^k-1的二叉树，称为满二叉树（每一层的结点都是最大结点数）。 （2） ...
二叉树binaryTree遍历规则
qq_35490520的博客
07-15 209
点击打开链接如图所示二叉树：  前中后是针对于根节点而言的。跟结点最先被访问即为前序遍历；根节点在左右子结点之间被访问，即为中序遍历；根节点最后被访问，即为后序遍历。对于每一棵子树而言，遍历时也需要按照所指定的遍历规则进行遍历，是一种递归的遍历方式。前序遍历：记为根左右，若二叉树为空，则结束返回。前序遍历的规则：访问根节点前序遍历左子树前序遍历右子树注意：在完成第2,3步的时候，也是要按照前序遍历...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值