LintCode-140: Fast Power

最新推荐文章于 2019-10-21 17:40:42 发布

原创最新推荐文章于 2019-10-21 17:40:42 发布 · 479 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#LintCode

algorithm-design 专栏收录该内容

817 篇文章

订阅专栏

本文介绍了一种快速计算a^n%b的方法，适用于a、b、n均为32位非负整数的情况。通过利用取模运算的特殊性质，采用递归和迭代两种方式实现了快速幂取模算法。文章还提供了代码示例并解释了算法背后的数学原理。

Fast Power

Calculate the a^n % b where a, b and n are all 32bit non-negative integers.

Example
For 2^31 % 3 = 2

For 100^1000 % 1000 = 0

Challenge
O(logn)

这题可以和pow(n)那题对照学习。
本题要注意用到异或的这个特性：
(a * b) % p = ((a % p) * (b % p)) % p
不然直接求a^n肯定溢出。

注意，类似的取模性质还有：
(a * b) % m = a * (b % m) % m
(a ^ b) % m = (a % m) ^ b % m

解法1：递归版。

    int fastPower(int a, int b, int n) {
        if (n<0) return -1;
        if (n==0) return 1%b;  //note (32^0)%1=0, as 1%1=0 (in case b=1)
        if (n==1) return a%b;
        
        long long result=fastPower(a,b,n/2);
        result=result*result%b;
        if (n&0x1) result=result*a%b;
        return (int) result;
    }

解法2：迭代版。
下面的证明引用自
https://blog.youkuaiyun.com/gao1440156051/article/details/40706893
进一步研究指数b的二进制表示发现，对任意的整数b都可表示为：
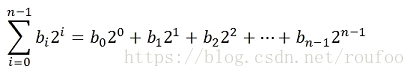
这里写图片描述

n表示b的实际二进制位数
bi表示该位是0或1
因此，a^b可表示为：

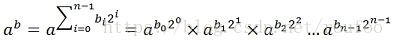
这里写图片描述

即用b的每一位表示a的每一项，而对任意相邻的两项存在平方关系，即：

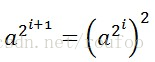
这里写图片描述

因此我们构造下面的算法：

把b转换为二进制表示，并从右至左扫描其每一位（从低到高）
当扫描到第i位时，根据计算a的第i项的模，这里先是假设多有的bi都是1，记录下来，当真正的bi为1时供result使用
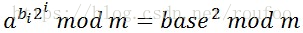
这里写图片描述

base变量表示第i-1位时计算出的模。
如果第i位为1，即bi=1,则表示该位需要参与模运算，计算结果 result = (result*base) mod m;其中result为前i-1次的计算结果。
之前的pow(n)那题也是用了这个思路。

下面的代码源自九章：
注意代码里面的b实际上是上面的m，代码里面的n是上面的b。

  public int fastPower(int a, int b, int n) {
        long ans = 1, tmp = a;
        
        while (n != 0) {
            if (n % 2 == 1) {
                ans = (ans * tmp) % b;
            }
            tmp = (tmp * tmp) % b;
            n = n / 2;
        }
        
        return (int) ans % b;
    }

代码同步在
https://github.com/luqian2017/Algorithm