学习C/C++语言系列（2）栈_c++栈的实现与测试-优快云博客

栈是什么

栈是一种特殊的线性表，特殊在哪呢？特殊在于栈上的空间只能后进先出，即最后进来的只能最先出去。这就好比硬币管里的硬币，只能先拿出最后放出去的。

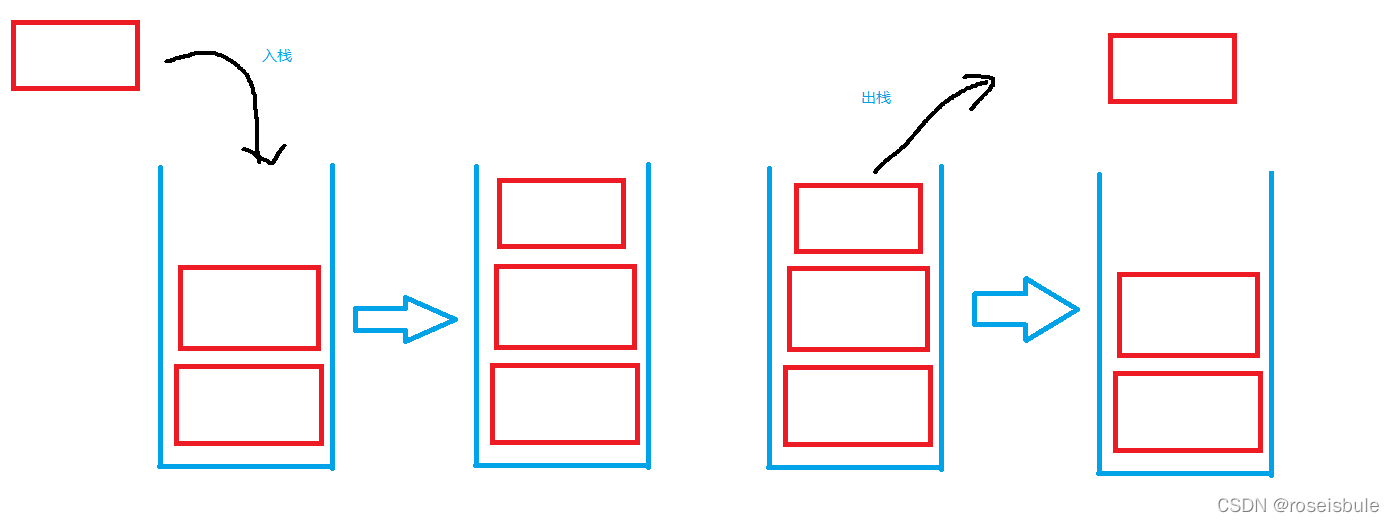
这种后进先出的原则就叫做Last In First Out(LIFO)。

栈的C语言实现

栈的实现既可以用数组实现，也可以用单链表来实现。相对来讲，数组的实现更优，因为数组在尾部插入数据并不需要遍历，而且数组因为是连续存放缘故，缓存命中率更高。

栈的具体实现

先来简单思考一下，我们的栈要实现哪些基本功能。1.希望能把栈上的元素给我打印出来（测试用）。2.希望能有初始化一个栈的函数。3.希望能有一个入栈的函数。4.希望有一个出栈的函数。5.给出栈顶元素的函数。6.给出栈中有效元素个数的函数。7.判断栈是否为空的函数。8.销毁栈的函数。

这些其实和顺序表是很像的，唯一不同的就是栈只能后进先出。

栈的定义

为方便后续修改存储的数据类型，将int进行改名。

typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int top; // 栈顶
	int capacity; // 容量
}Stack;

初始化栈

这里我倾向于在初始化的时候给个初始空间，这样在后续入栈上就不需要去判断是否没有空间。

// 初始化栈
void StackInit(Stack* ps)
{
	assert(ps);
	STDataType* tmp = (STDataType*)malloc(sizeof(STDataType) * 2);
	if (tmp == NULL)
	{
		printf("Malloc Fail In StackInit\n!");
		exit(-1);
	}
	ps->a = tmp;
	ps->top = -1;// top为栈顶元素的下标
	ps->capacity = 2;
}

入栈

入栈也是很简单的，需要注意的是要判断栈的空间是不是满了。

// 入栈
void StackPush(Stack* ps, STDataType data)
{
	assert(ps && ps->a);
	if (ps->top == ps->capacity - 1)
	{
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * (ps->capacity) * 2);
		if (tmp == NULL)
		{
			printf("Realloc Fail In StackPush!\n");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity *= 2;//初始化给了初始空间后 这里就不需要判断capacity是否为0
	}
	(ps->a)[++(ps->top)] = data;
}

出栈

出栈更简单，因为不需要去干什么操作，top--即可。top记录的是有效数据，只要不有效，管他是什么值都没用，top就是它的顶。

// 出栈
void StackPop(Stack* ps)
{
	assert(ps && ps->a);
	if (ps->top == -1)
		return;
	//不需要free 可以直接覆盖
	(ps->top)--;
}

获取栈顶元素

// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
	assert(ps && ps->a);
	assert(ps->top != -1);
	return (ps->a)[ps->top];
}

检测和显示函数

// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
	assert(ps && ps->a);
	return ps->top + 1;
}

// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0
int StackEmpty(Stack* ps)
{
	assert(ps && ps->a);
	return ps->top == -1 ? 1 : 0;
}

// 销毁栈
void StackDestroy(Stack* ps)
{
	assert(ps && ps->a);
	free(ps->a);
	ps->a = NULL;
}

// 显示栈中元素
void StackPrint(Stack* ps)
{
	assert(ps && ps->a);
	if (ps->top == -1)
	{
		printf("Nothing!\n");
		return;
	}
	for (int i = 0; i <= ps->top; i++)
		printf("%d ", ps->a[i]);
	printf("\n");
}

最后

最后呢，我们来测试一下栈有没有出错的地方，测试一下。

void test()
{
	Stack st;
	StackInit(&st);
	StackPush(&st, 1);
	StackPush(&st, 2);
	StackPush(&st, 3);
	StackPush(&st, 4);
	StackPush(&st, 5);
	StackPush(&st, 6);
	StackPrint(&st);
	StackPop(&st);
	StackPrint(&st);
	StackPop(&st);
	StackPrint(&st);
	StackPop(&st);
	StackPrint(&st);
	StackPop(&st);
	StackPrint(&st);
	printf("%d\n", StackEmpty(&st));

	StackPop(&st);
	StackPop(&st);

	printf("%d\n", StackEmpty(&st));
	StackDestroy(&st);
	StackInit(&st);

	printf("%d\n", StackEmpty(&st));

}


int main()
{
	test();
	return 0;
}

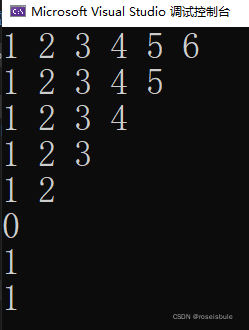
ok，没用什么严重错误，都跑起来了。但是有了顺序表为啥还要有栈呢，我们来看下面这道题目。

用栈解决有效括号检测匹配问题

这是一道leetcode上面的题目：力扣

思路

其实我们随便写一个带括号的式子来观察一下。如：(((()))())。当然我这里这里只有小括号，其他的括号也是一样的。

我们可以发现一个规律，那就是一个右边是右括号的左括号，两个一定相等。如果我们重复的不停的消除这一对对括号，最后将不剩下括号，符合这样的要求的表达式，它的括号分布一定是有效的。

这段话可能有点绕，看下图。

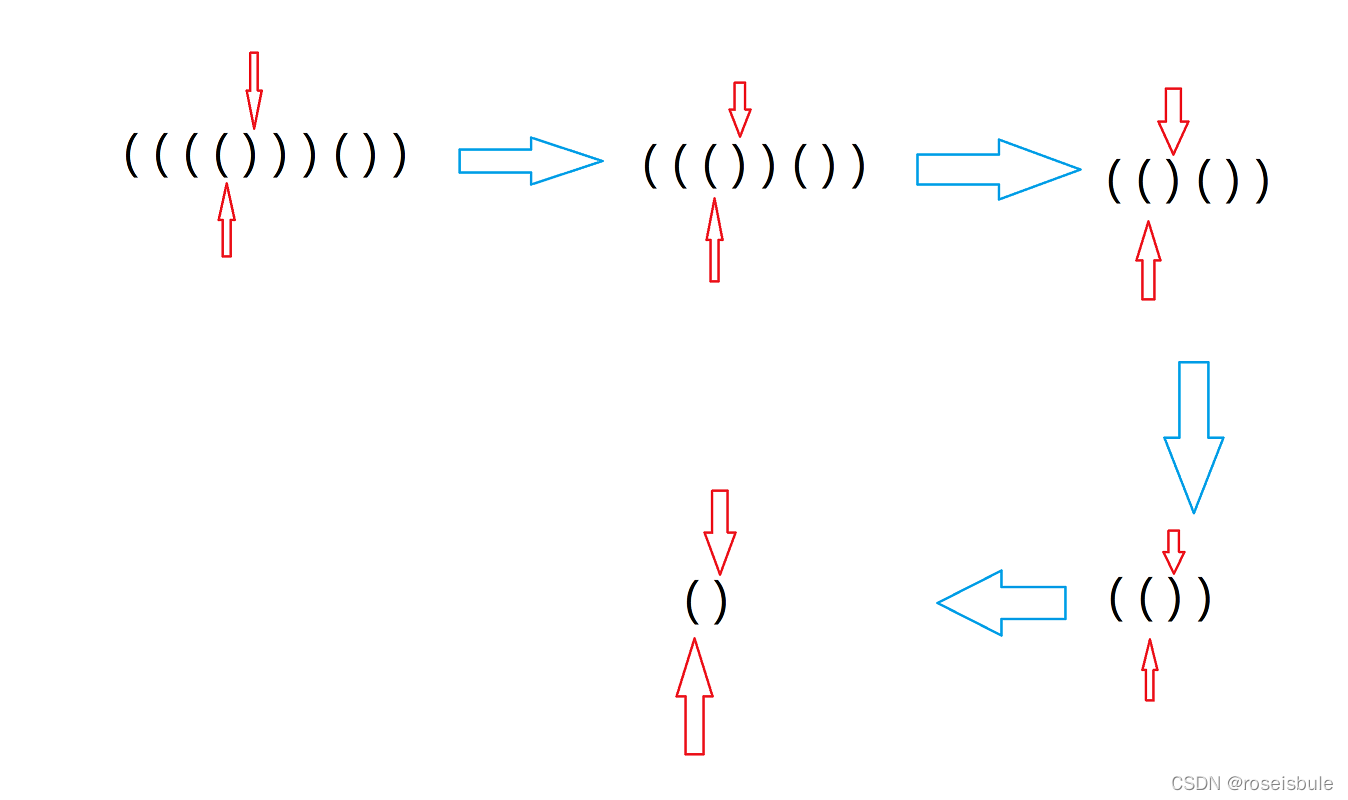
我们不停地从头开始碰到一个右边是右括号的左括号则将二者一起消除。最后，如果这个式子的括号分布是有效的，将会得到空，换言之如果最后找不到符合条件的左括号，但式子中仍有括号，则不有效。

那么，如何用栈去解决这个问题呢？

我们可以这样，如果是一个左括号，我们把这个左括号放到栈上去，然后继续遍历，如果是右括号，那么就让这个右括号前的左括号出栈。由于栈只能后进先出，所以这个出的一定是这个右括号前一个左括号，然后继续遍历，重复这样的操作。这是不是相当于上面讲到的绑定消除呢？进行到最后，怎么判断是否有效呢？如果此时栈中没用左括号了，那说明左括号都被消除了，可以说明是有效的。这种判断能判对大部分情况，但是有一种情况例外，那就是只有右括号。所以我们在碰到右括号的时候要判断一下，栈中有没有左括号，如果没有左括号，但是却喷到个右括号，所以肯定不行。

代码实现

由于，C没有栈的库，所以必须要自己实现一个栈。

在这里呢，我用的栈函数都是上面用到的函数，这里只给出关键函数。而且注意，STDataType要改成char。

bool isValid(char* s)
{
	Stack st;
	StackInit(&st);
	while (*s != '\0')
	{
		if (*s == ')' || *s == ']' || *s == '}')
		{
			if (StackEmpty(&st))
				return false;
			else
			{
				if ((*s == ')' && StackTop(&st) != '(')
					|| (*s == ']' && StackTop(&st) != '[')
					|| (*s == '}' && StackTop(&st) != '{')
					)
					return false;
				else
					StackPop(&st);
			}
		}
		else
			StackPush(&st, *s);
		s++;
	}
	if (StackEmpty(&st))
		return true;
	return false;
}