打卡信奥刷题（1564）用C++实现信奥 P6459 [COCI 2006/2007 #5] TENIS-优快云博客

本文链接：https://blog.youkuaiyun.com/rogeliu/article/details/148859894

P6459 [COCI 2006/2007 #5] TENIS

题目描述

两个球员正常进行一次网球比赛，比赛由 $n$ 轮组成，每一轮都会进行 $1\sim 5$ 次对决不等。每次对决的结果用 A:B 表示，其中 A 为第一个球员的获胜场次，B 为第二个球员的获胜场次。

比赛有以下规则：

如果其中一个球员获胜了 $6$ 个球及以上，并且他比另一个球员至少多获胜两个球，那么这一次对决他就胜利了。
此外，如果第一、二次对决的结果都是 6:6 那么将会进行一轮决赛来准确的得出一位球员获胜。
当有一名球员获胜两次对决时，他就是这轮比赛的胜者，且这轮比赛结束。

如果一轮比赛按照上述规则顺利进行，并且最终得以结束，那么我们就认为这轮是有效的。

但是，有一名特殊的球员—— federer,他不会输掉任意一次对决。（因为我们知道他来自外太空…）

你需要检验这 $n$ 轮比赛是否有效。

输入格式

输入第一行两个字符串，用空格隔开，表示两名参赛的选手。

第二行为一个整数 $n$ ，表示一共进行了 $n$ 轮比赛。

接下来的 $n$ 行，每行有 $1\sim 5$ 个形如 A:B 的对决结果。保证 A B 是介于 $0\sim 99$ 之间的整数。

输出格式

输出共 $n$ 行。

对于每轮比赛，输出 da 表示结果有效或输出 ne 表示结果无效。

输入输出样例 #1

输入 #1

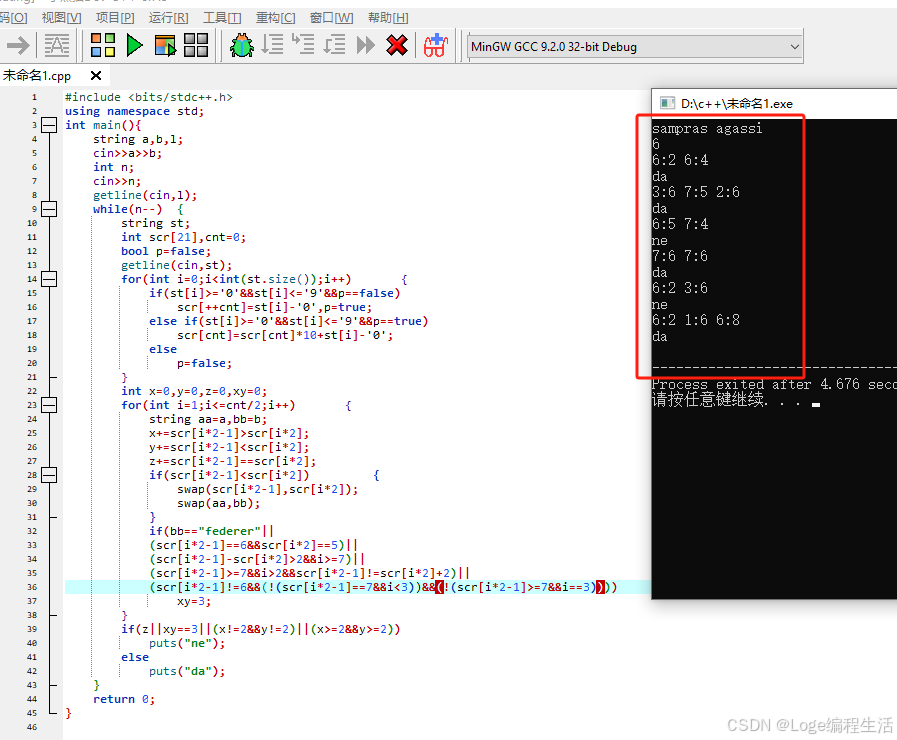
sampras agassi
6
6:2 6:4
3:6 7:5 2:6
6:5 7:4
7:6 7:6
6:2 3:6
6:2 1:6 6:8

输出 #1

da
da
ne
da
ne
da

输入输出样例 #2

输入 #2

federer roddick
1
2:6 4:6

输出 #2

ne

说明/提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 50$ 。

说明

题目译自 COCI2006-2007 CONTEST #5 T3 TENIS。

C++实现

#include <bits/stdc++.h>
using namespace std;
int main(){
	string a,b,l;
	cin>>a>>b;
	int n;
	cin>>n;
	getline(cin,l);
	while(n--)	{
		string st;
		int scr[21],cnt=0;
		bool p=false;
		getline(cin,st);
		for(int i=0;i<int(st.size());i++)		{
			if(st[i]>='0'&&st[i]<='9'&&p==false)
				scr[++cnt]=st[i]-'0',p=true;
			else if(st[i]>='0'&&st[i]<='9'&&p==true)
				scr[cnt]=scr[cnt]*10+st[i]-'0';
			else
				p=false;
		}
		int x=0,y=0,z=0,xy=0;
		for(int i=1;i<=cnt/2;i++)		{
			string aa=a,bb=b;
			x+=scr[i*2-1]>scr[i*2];
			y+=scr[i*2-1]<scr[i*2];
			z+=scr[i*2-1]==scr[i*2];
			if(scr[i*2-1]<scr[i*2])			{
				swap(scr[i*2-1],scr[i*2]);
				swap(aa,bb);
			}
			if(bb=="federer"||
			(scr[i*2-1]==6&&scr[i*2]==5)||
			(scr[i*2-1]-scr[i*2]>2&&i>=7)||
			(scr[i*2-1]>=7&&i>2&&scr[i*2-1]!=scr[i*2]+2)||
			(scr[i*2-1]!=6&&(!(scr[i*2-1]==7&&i<3))&&(!(scr[i*2-1]>=7&&i==3))))
				xy=3;
		}
		if(z||xy==3||(x!=2&&y!=2)||(x>=2&&y>=2))
			puts("ne");
		else
			puts("da");
	}
	return 0;
}