B4070 [GESP202412 五级] 奇妙数字
题目描述
小杨认为一个数字 xxx 是奇妙数字当且仅当 x=pax=p^ax=pa,其中 ppp 为任意质数且 aaa 为正整数。例如,8=238=2^38=23,所以 888 是奇妙的,而 666 不是。
对于一个正整数 nnn,小杨想要构建一个包含 mmm 个奇妙数字的集合 {x1,x2,⋯ ,xm}\{x_1,x_2,\cdots,x_m\}{x1,x2,⋯,xm},使其满足以下条件:
- 集合中不包含相同的数字。
- x1×x2×⋯×xmx_1\times x_2\times \cdots\times x_mx1×x2×⋯×xm 是 nnn 的因子(即 x1,x2,⋯ ,xmx_1,x_2,\cdots,x_mx1,x2,⋯,xm 这 mmm 个数字的乘积是 nnn 的因子)。
小杨希望集合包含的奇妙数字尽可能多,请你帮他计算出满足条件的集合最多包含多少个奇妙数字。
输入格式
第一行包含一个正整数 nnn,含义如题面所示。
输出格式
输出一个正整数,代表满足条件的集合最多包含的奇妙数字个数。
输入输出样例 #1
输入 #1
128
输出 #1
3
说明/提示
样例解释
关于本样例,符合题意的一个包含 333 个奇妙数字的集合是 {2,4,8}\{2,4,8\}{2,4,8}。首先,因为 2=212=2^12=21,4=224=2^24=22,8=238=2^38=23,所以 2,4,82,4,82,4,8 均为奇妙数字。同时,2×4×8=642\times 4\times 8=642×4×8=64 是 128128128 的的因子。
由于无法找到符合题意且同时包含 444 个奇妙数字的集合,因此本样例的答案为 333。
数据范围
对于 100%100\%100% 的数据,保证 2≤n≤10122\le n\le 10^{12}2≤n≤1012。
| 子任务编号 | 得分占比 | nnn |
|---|---|---|
| 111 | 20%20\%20% | ≤10\le 10≤10 |
| 222 | 20%20\%20% | ≤1 000\le 1\,000≤1000 |
| 333 | 60%60\%60% | ≤1012\le 10^{12}≤1012 |
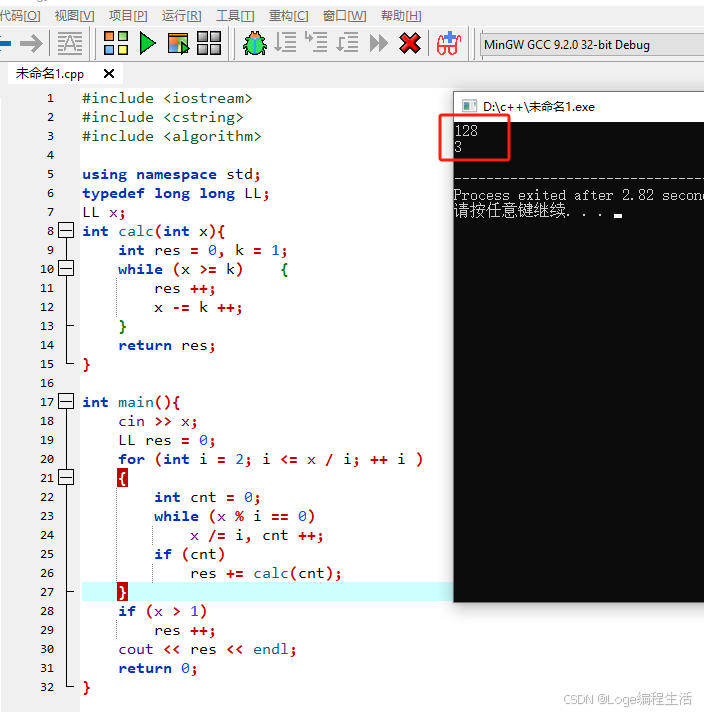
C++实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL x;
int calc(int x){
int res = 0, k = 1;
while (x >= k) {
res ++;
x -= k ++;
}
return res;
}
int main(){
cin >> x;
LL res = 0;
for (int i = 2; i <= x / i; ++ i )
{
int cnt = 0;
while (x % i == 0)
x /= i, cnt ++;
if (cnt)
res += calc(cnt);
}
if (x > 1)
res ++;
cout << res << endl;
return 0;
}
后续
接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现,记录日常的编程生活、比赛心得,感兴趣的请关注,我后续将继续分享相关内容





















 1869
1869

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








