打卡信奥刷题（1328）用C++实现信奥 P3182 [HAOI2016] 放棋子

P3182 [HAOI2016] 放棋子

题目描述

给你一个 $N\times N$ 的矩阵，每行有一个障碍，数据保证任意两个障碍不在同一行，任意两个障碍不在同一列，要求你在这个矩阵上放 $N$ 枚棋子（障碍的位置不能放棋子），要求你放 $N$ 个棋子也满足每行只有一枚棋子，每列只有一枚棋子的限制，求有多少种方案。

输入格式

第一行一个 $N$，接下来一个 $N\times N$ 的矩阵。$N\le 200$，0 表示没有障碍，1 表示有障碍。

输出格式

一个整数，即合法的方案数。

输入输出样例 #1

输入 #1

2
0 1
1 0

输出 #1

1

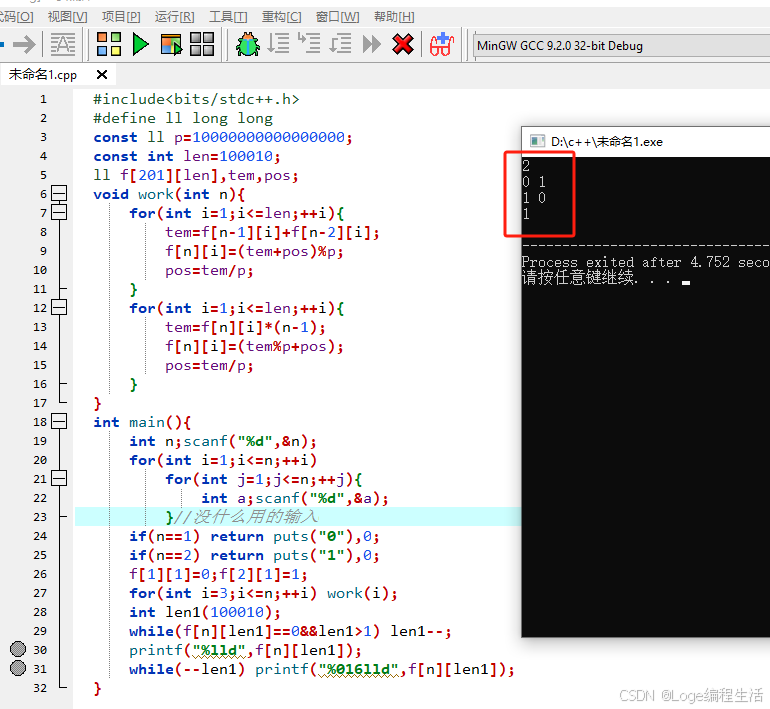
C++实现

  #include<bits/stdc++.h>
  #define ll long long
  const ll p=10000000000000000;
  const int len=100010;
  ll f[201][len],tem,pos;
  void work(int n){
      for(int i=1;i<=len;++i){
          tem=f[n-1][i]+f[n-2][i];
          f[n][i]=(tem+pos)%p;
          pos=tem/p;
      }
      for(int i=1;i<=len;++i){
          tem=f[n][i]*(n-1);
          f[n][i]=(tem%p+pos);
          pos=tem/p;
      }
  }
  int main(){
      int n;scanf("%d",&n);
      for(int i=1;i<=n;++i)
          for(int j=1;j<=n;++j){
              int a;scanf("%d",&a);
          }//没什么用的输入
      if(n==1) return puts("0"),0;
      if(n==2) return puts("1"),0;
      f[1][1]=0;f[2][1]=1;
      for(int i=3;i<=n;++i) work(i);
      int len1(100010);
      while(f[n][len1]==0&&len1>1) len1--;
      printf("%lld",f[n][len1]);
      while(--len1) printf("%016lld",f[n][len1]);
  }

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容