打卡信奥刷题（405）用C++信奥B3878[普及组/提高] [信息与未来 2015] 连续数的和

[信息与未来 2015] 连续数的和

题目描述

给出两个整数 $n$ 和 $k$，求出 $1\sim n$ 中连续 $k$ 个数的和为完全平方数的个数。

输入格式

一行两个整数 $n,k$。

输出格式

一行一个整数，即 $1\sim n$ 中连续 $k$ 个数的和为平方数的个数。

样例 #1

样例输入 #1

10 3

样例输出 #1

1

提示

样例解释

在 $1\sim 10$ 中，连续 $3$ 个数的和有：

• $1+2+3=6$；
• $2+3+4=9=3^2$；
• $3+4+5=12$；
• $4+5+6=15$；
• $5+6+7=18$；
• $6+7+8=21$；
• $7+8+9=24$；
• $8+9+10=27$。

故只有 $1$ 个。

数据范围

$2\le n\le 7\times 10^4,1\le k\le n$。

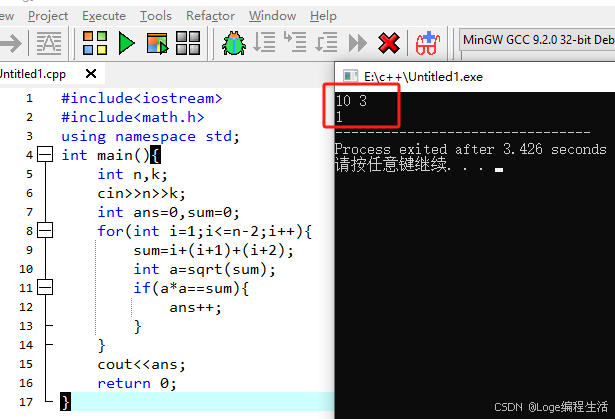
C++实现

#include
#include<math.h>
using namespace std;
int main(){
int n,k;
cin>>n>>k;
int ans=0,sum=0;
for(int i=1;i<=n-2;i++){
sum=i+(i+1)+(i+2);
int a=sqrt(sum);
if(a*a==sum){
ans++;
}
}
cout<<ans;
return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容