强化学习第五课 —— A2C & A3C：并行化是如何杀死经验回放

在 DQN 称霸的时代，我们为了解决强化学习中样本**“非独立同分布（Non-IID）”**的问题，不得不引入了一个巨大的外挂硬盘——经验回放池（Experience Replay Buffer）。

然而，2016 年 DeepMind 推出 A3C（Asynchronous Advantage Actor-Critic），就像一道闪电划破夜空。它告诉我们：只要你的“分身”够多，你就不需要“记忆”。

A3C 和随后 OpenAI 改进的 A2C，不仅是 Actor-Critic 架构的集大成者，更是一次关于**“并行计算如何改变算法收敛性”**的数学实验。

今天，我们深入公式内部，拆解并行化带来的质变。

---

一、回顾 Actor-Critic 的数学痛点

在进入并行化之前，我们必须先写出 Actor-Critic (AC) 的核心目标函数。AC 架构由两个网络组成：

1. Actor (${\pi }_{\theta }$)：负责输出动作概率。
2. Critic ($V_w$)：负责评价状态价值。

我们优化的目标是最大化期望回报 $J(\theta )$。根据策略梯度定理，Actor 的梯度更新公式为：

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{s_t,a_t\sim \pi }\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)\cdot A(s_t,a_t)\right]$$

其中，$A(s_t,a_t)$ 是优势函数（Advantage Function），它衡量了“在这个状态下选动作 $a_t$，比平均情况好多少”。在实际计算中，我们用 TD Error 来估计它：

$$A(s_t,a_t)\approx r_t+\gamma V_w(s_{t+1})-V_w(s_t)$$

痛点在于：
如果不使用 Replay Buffer，单个 Agent 产生的数据是高度**时间相关（Temporally Correlated）**的。
$$s_t\to s_{t+1}\to s_{t+2}\dots$$
这种强相关性会导致梯度下降的方向跑偏（Bias），让神经网络陷入局部最优或震荡。但如果使用 Replay Buffer，我们又变成了 Off-Policy（异策略），这在处理连续动作或复杂策略时往往不稳定。

A3C 的出现，就是为了解决这个悖论：如何在 On-Policy（在线策略）的前提下，打破数据相关性？

---

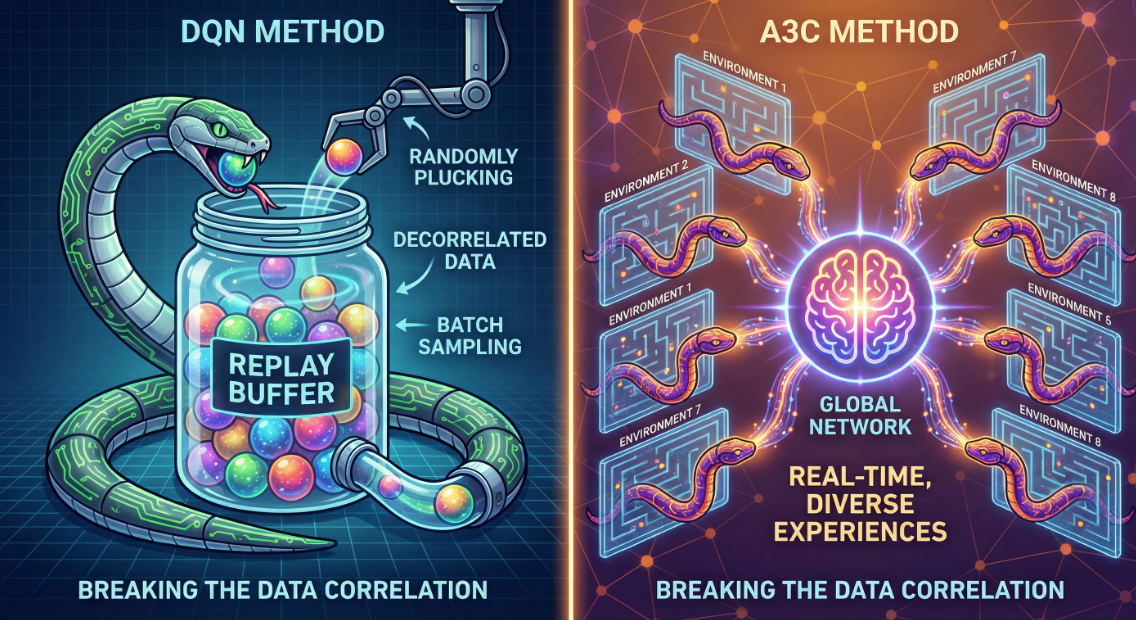
二、A3C：多线程的梯度异步轰炸

A3C 的全称是 Asynchronous Advantage Actor-Critic。它的核心逻辑是：创建多个 Worker（子线程），每个 Worker 拥有独立的完整环境实例。

1. N-Step 回报：平衡偏差与方差

A3C 并不使用单步 TD，而是通常使用 N-Step Return 来计算目标值。这可以让奖励传播得更快。
对于某个 Worker，在 $t$ 时刻，它向前探索 $n$ 步，计算截断的累积回报 $G_t^{(n)}$：

$$G_t^{(n)}=\sum _{k=0}^{n-1}{\gamma }^k{r}_{t+k}+{\gamma }^n{V}_w(s_{t+n})$$

这里，前 $n$ 步是真实的奖励（低偏差，高方差），最后加上的是 Critic 的预测值 $V_w(s_{t+n})$（引入偏差，降低方差）。

2. 损失函数的构造

每个 Worker 独立计算累积梯度。总损失函数 $L$ 由三部分组成：策略损失、价值损失和熵正则项。

$$L=\underset{\text{Policy Loss}}{\underbrace{L_{\pi }}}+\frac{1}{2}\underset{\text{Value Loss}}{\underbrace{L_v}}-\beta \underset{\text{Entropy}}{\underbrace{H(\pi )}}$$

展开来看：

• 策略梯度损失（我们要最大化目标，所以 Loss 加负号）：
  $$L_{\pi }=-\log {\pi }_{\theta }(a_t|s_t)\cdot (G_t^{(n)}-V_w(s_t))$$
  (注意：这里的 $G_t^{(n)}-V_w(s_t)$ 即为 N-step 的优势函数估计)

• 价值函数损失（MSE）：
  $$L_v=(G_t^{(n)}-V_w(s_t){)}^2$$

• 熵正则项（鼓励探索，防止过早收敛）：
  $$H(\pi )=-\sum {\pi }_{\theta }(a|s_t)\log {\pi }_{\theta }(a|s_t)$$

3. 异步更新（Hogwild!）

这是 A3C 最狂野的地方。Worker 计算出梯度 $d\theta$ 后，直接推送到全局网络（Global Network）：

$${\theta }_{global}\leftarrow {\theta }_{global}-\eta \cdot \nabla L({\theta }_{worker})$$

然后，Worker 立刻把最新的 ${\theta }_{global}$ 复制回自己身上，继续跑。
关键点： 这个过程是异步的，没有锁（Lock-free）。这意味着 Worker A 更新参数时，Worker B 可能正在用旧参数计算梯度。
这种“混乱”不仅没有毁掉算法，反而引入了额外的噪声，起到了类似 SGD 中噪声的作用，帮助逃离局部极小值。

---

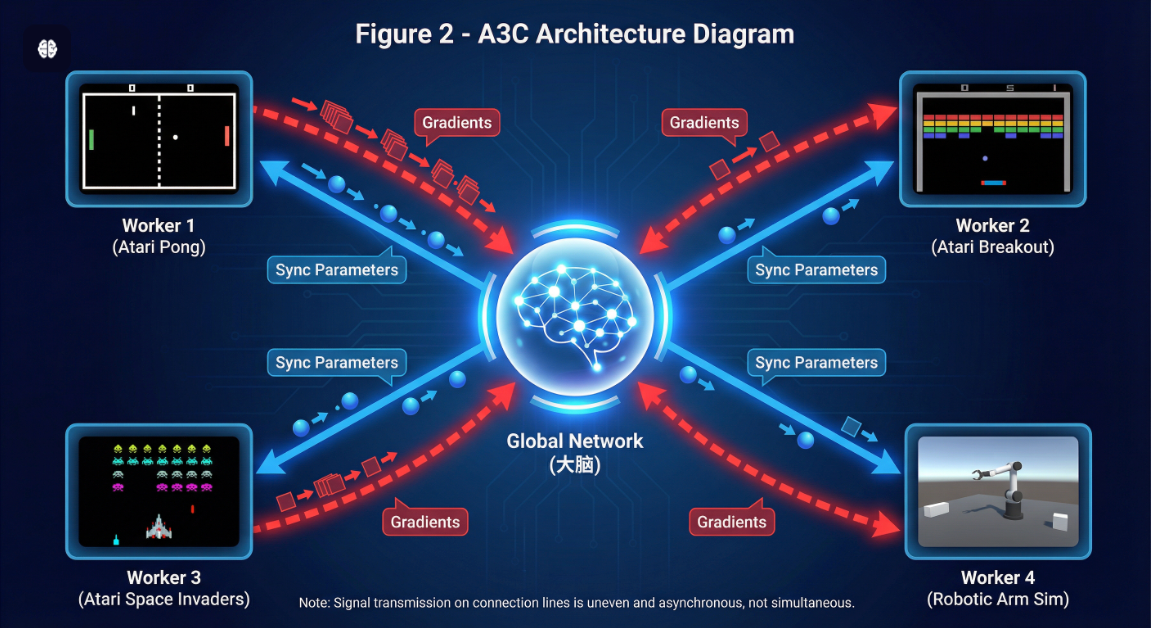
三、A2C：同步的理性回归

A3C 很强，但 Google DeepMind 的工程师在实现时发现：异步编程太痛苦了，而且 Python 的多线程受到 GIL（全局解释器锁）的限制，很难利用 GPU 的并行加速能力。

OpenAI 的研究者后来提出了 A2C (Advantage Actor-Critic)，去掉了第一个 “Asynchronous”。他们发现：异步并不是必须的，并行才是核心。

1. 同步更新机制

A2C 让所有 Worker 必须“齐步走”。

1. 所有 Worker 并行执行动作，产生一批数据。
2. 等到所有 Worker 都完成一步（或 n 步）后。
3. 将所有数据打包成一个 Batch。
4. 利用 GPU 对这个大 Batch 进行一次高效的前向和反向传播。

2. 数学上的等价性

A2C 的梯度更新本质上是所有 Worker 梯度的平均值：

$${\nabla }_{\theta }J(\theta {)}_{batch}=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }J(\theta {)}_i$$

这在数学上比 A3C 更稳健。A3C 因为参数滞后（Laggy Updates），其实是在优化一个“过时”的策略，而 A2C 保证了当前计算梯度的策略和产生数据的策略是完全一致的。

公式对比：

• A3C: ${\theta }_{t+1}={\theta }_t+\alpha \nabla J({\theta }_{t-\tau })$ (存在 $\tau$ 的延迟)
• A2C: ${\theta }_{t+1}={\theta }_t+\alpha \frac{1}{N}\sum \nabla J_i({\theta }_t)$ (无延迟)

---

四、并行化到底带来了什么？

我们回到标题。并行化（无论是 A3C 还是 A2C）到底解决了什么根本问题？

1. 遍历性的增强 (Ergodicity)

在数学上，强化学习希望 Agent 能够遍历状态空间 $S$。单智能体容易陷入环境的某一个死角（Sub-optimal policy）。
$$P(s|{\pi }_{parallel})\approx \frac{1}{N}\sum P(s|{\pi }_i)$$
$N$ 个智能体同时在探索不同的角落，相当于极大地拓宽了采样分布的支撑集（Support），这让神经网络能学到更普适的特征，而不是死记硬背某一条路径。

2. 替代经验回放 (Replacing Experience Replay)

DQN 需要 Replay Buffer 来打破 $Correlation(s_t,s_{t+1})$。
A3C/A2C 通过并行采样，使得在一个 Batch 内的数据来源是：
$$Batch=\{(s_t^1,a_t^1),(s_t^2,a_t^2),\dots ,(s_t^N,a_t^N)\}$$
因为环境 $1$ 和环境 $N$ 是独立的，所以 $Correlation(s_t^1,s_t^N)\approx 0$。
这使得我们可以在 On-Policy 的条件下，直接训练网络，而不需要在内存中存储数百万条过期的历史数据。

---

结语：算力换算法的胜利

A2C 和 A3C 的故事告诉我们，有时候数学上的难题（数据相关性、非平稳性），可以通过系统架构上的改变（并行化）来优雅解决。

从公式上看，它们只是在 Policy Gradient 的基础上加了一个求和符号 $\sum$；但从本质上看，它们开启了**大规模分布式强化学习（Distributed RL）**的先河。后来的 PPO、IMPALA 甚至 AlphaStar，其根基都植根于这种并行采样的思想之中。

掌握 A2C，你就不再只是在训练一个 Agent，你是在指挥一支军团。