计算机组织结构 随笔 【3】

第三话 流水线技术

内容导读

• 流水线的基本概念和分类
• 流水线的性能标准（超级重点）
• 流水线设计的障碍
• 流水线的调度问题（重点）
• 流水线的相关和冲突（重点）

流水线的基本概念和分类

工厂里面的流水线是这样子的：

产品在流水线上被按顺序完成多个工序。
如果把流水线反映到计算机的任务中，工序叫做流水线的段/级，工序的数量叫做流水线的深度。

假如把求浮点数加法的算法步骤分类可以分为：

我们画出时空图（纵坐标是空间，横坐标是时间）：
工序有四步，所以有四个段，我们把段写到纵坐标上，然后假设有多个浮点数加法操作需要完成。时空图如下：

只用了7个$\Delta t$此时完成了4个浮点数加法的操作。在时空图里面的数字表示任务的索引。

流水线的分类可以根据任务等级的不同分为：部件级别流水线，处理机流水线，系统级别流水线。目前我们主要关注的是处理机的流水线，也叫做指令流水线。

根据在流水线实现的功能，可以分为：单功能流水线和多功能流水线。单功能流水线就是上面关于浮点数加法的例子。

多功能流水线如下例子：

流水线也分为静态流水线和动态流水线，划分的标准是流水线实现任务的时候是固定的还是可以参杂其他任务的步骤进来。（继续以浮点加法和顶点乘法作为例子）
这是静态的：

这是动态的：

但无论怎样需要注意的是，在同一列里面是不会出现同一个任务的。

还有，我们会听到线性流水线和非线性流水线，区别在于，是否有回路。非线性流水线如下：

顺序流水线和乱序流水线的区别在于：输入任务的顺序和输出任务的顺序是否一致。

流水线的性能标准

我们对一条流水线的好坏需要有一个评判的标准，我们会从三个角度去分析：吞吐率TP，加速比S，效率E。

• “吞吐率” 描述：单位时间内流水线完成的任务数量
• “加速比” 描述：流水线的耗时和顺序执行耗时的比值
• “效率” 描述：有效的占用域和总的时空区面积比值

Tips: 记住上述的描述比记住公式要靠谱，因为公式根据题目意思会变的，不固定的，请深刻理解上述描述。

下面我们将对时空图进行计算分析，默认以下字母表达：

• 段数（步骤数，纵坐标的数量）= $k$
• 任务数 = $n$

（如上图的k=4）

吞吐率的计算
TP是指单位时间内流水线完成任务的数量，自然的，分母就是总的执行时间，实际吞吐率：
$$TP=\frac{n}{(k+n-1)\Delta t}$$

最大吞吐率$T{P}_{max}=li{m}_{n\to \infty }TP$，虽大吞吐率我们当然希望在单位时间内能完成的任务越多越好了。

吞吐率瓶颈处理
在动态流水线里面有可能会出现瓶颈，什么叫做瓶颈？如下图，找一下不和谐的地方：

这里明显凸出来了，如果我们按照TP的计算方法得到的如下：(假设长的$\Delta T=3\Delta t$)
$$TP=\frac{n}{(k+n-1)3\Delta t}$$

被浪费的时空区（红色的地方）：

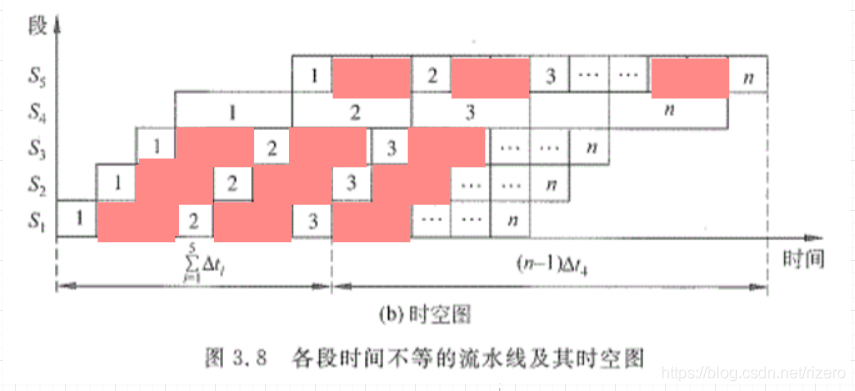
如我们所见，实际上，上图有非常多的浪费，这样会变成最长的T会卡住我们的吞吐率，所以我们叫做瓶颈段，变相决定了吞吐率。这当然是不允许了，我们要想办法对时空图进行改进，我们思考一下，为什么会出现浪费？

因为$T_{Long}=3n\Delta t$，需要到3次的短的T才能满足匹配。既然我们想把n统一，我们可以增加某一个段的并行处理。思想如下图：

在第四步，我们有三个可以同时处理的工人，这样一来，就能把瓶颈段消除掉了。修改之后的时空图如下：

看上面这个时空图，是不是顺眼多了，此时我们再计算TP
$$TP=\frac{n}{(k+n-1)\Delta t}$$
可见，瓶颈段被消除了。

加速比的计算
加速比的计算是最简单的，就是当前耗时和顺序执行耗时的比值：
$$S=\frac{(k+n-1)\Delta t}{kn\Delta t}$$

效率的计算
效率实际上就是时空区的有效率，在图上哪些地方被浪费了？就是流水线的排入和排出的时间被浪费了。

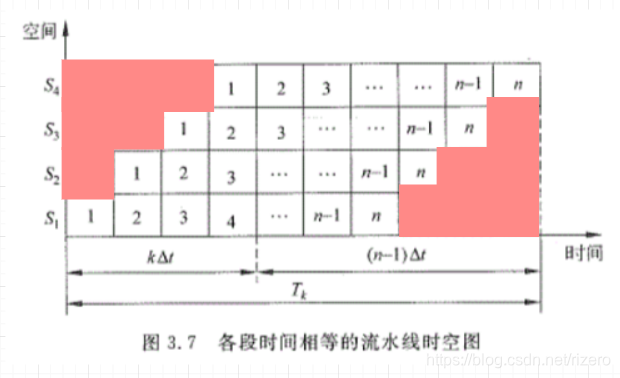
计算效率就是计算面积比：不是红色的地方和总的面积的比值。
$$E=\frac{nk\Delta s}{k(k+n-1)\Delta s}$$

静态流水线分析
假如我们需要在流水线部件（如下所示）计算${\prod }_{i=1}^4(A_i+B_i)$

问计算吞吐率，加速比，效率。（要求使用静态流水线，静态流水线就是并行了某一种运算之后需要完全排空才能做其他运算）

解：
首先，我们需要分解这个运算步骤，这是累积计算，但在累积之前，我们要先求和。
$$\begin{gathered} (A_1+B_1)=P_1, \\ (A_2+B_2)=P_2, \\ (A_3+B_3)=P_3, \\ (A_4+B_4)=P_4, \\ {P}_1\ast P_2=V_1, \\ {P}_3\ast P_4=V_2, \\ result=V_1\ast V_2 \end{gathered}$$

我们可以把能够并列计算的步骤列出来，首先，4个加法的运算是可以并行处理的，然后2个乘法的发生可以并列出现，最后剩下1个乘法运算。

其实我们只需要记住这样一件事：数字是任务标签，纵坐标是步骤，就不会出错了。

如上图所示，4个并行的加法运算，2个并行的乘法运算，1个乘法运算，由于是静态流水线，所以必须排空所有才能进入新的运算环节。

接下来计算吞吐率TP，加速比S，效率E。
$$TP=\frac{7}{18\Delta t}$$
$$S=\frac{36\Delta t}{18\Delta t}=2$$
$$E=0.25$$

动态流水线的分析
有一条动态流水线由以下五段组成：加法用1，3，4，5段，乘法用1，2，5段，第四段的时间为2$\Delta t$，其余各段时间均为$\Delta t$，而且流水线的输出可以直接返回输入端或者暂存在相应的流水线寄存器，若在该流水线上计算${\sum }_{i=1}^4(A_i\ast B_i)$，求吞吐率，加速比，效率？

解：
老规矩，我们先对计算步骤来一个大解剖。
$$\begin{gathered} A_1\ast B_1=P_1 \\ {A}_2\ast B_2=P_2 \\ {A}_3\ast B_3=P_3 \\ {A}_4\ast B_4=P_4 \\ {P}_1+P_2=V_1 \\ {P}_3+P_4=V_2 \\ result=V_1+V_2 \end{gathered}$$

有4个可并列运算的乘法，2个可并列运算的加法，以及最后1个加法运算。

和上题不同的是这是一条动态流水线。
也就说，可以出现之前的运算没有排空的情况下，就能进行其他运算，只要对应的步骤段硬件空闲下来就行。

在4个乘法运算在进行的时候，我们只需要计算出P1和P2就可以开启加法任务，也就说下图的#1任务的开始。

$$TP=\frac{7}{16\Delta t}$$
$$S=\frac{27\Delta t}{16\Delta t}\approx 1.69$$
$$E=\frac{4\ast 3+3\ast 5}{5\ast 16}\approx 0.338$$

流水线设计的障碍

瓶颈段
在说吞吐率的时候已经提到过瓶颈段这个问题了，我们只需要把某一个步骤增加并行处理（就好比塞车了，把路修宽一个道理）

额外开销
比如流水线的寄存器延迟，时钟偏移开销等，这里就涉及到一个问题，是不是流水线的段数越多，流水线的性能越好呢？不是的，当流水线的段数增多的时候也会带来更多其他乱七八糟的开销，反而效率降低。

冲突问题
冲突问题本质上就是顺序的先后问题和单一对象访问占用问题。

流水线的调度问题

流水线的调度问题相对来说比较复杂，我们只讲单功能的非线性流水线调度问题，已经可以从中深刻体会流水线的调度思想了。

下面我将用最最通俗的大白话来讲述你们课本看不懂的流水线调度问题，看完不懂来打我。

疑惑1：流水线为什么会产生冲突？

首先，只有非线性流水线才需要调度，为什么呢？因为会产生过程冲突啊才需要调度的。

那我们继续想，为什么非线性流水线会产生过程冲突呢，而线性流水线不会有过程冲突呢？
我们要先弄懂非线性流水线是啥子玩意：非线性流水线是指有反馈回路的流水线，如下图（之前讲流水线分类的时候捎带提过一下）：

也就是说，一轮运算任务的结束，需要执行某些部件多次。这就有个问题了，假如说我们像线性流水线那样子源源不断给输入喂入任务，在线性流水线里面我们知道：一旦某个任务执行过第一个步骤就不会回头的，这和工厂的履带一样，不会倒着转的，但是非线性的流水线不同，他可能第一次执行该部件的结果来作为第二次的输入。

那非线性流水线的冲突到底是个什么样子呢？ 假设有如下的处理部件

可以假象一下：首先，第一个任务开始执行，经过S1，然后经过S2，好，此时如果按照线性流水线来说，不会倒着回去S1的，所以我们可以放心传入任务二

但是，很不幸的是非线性流水线倒着回来了，假设我们在第一个任务计算完S2的时候传入第二个任务，

那此时S1就纠结了，“哎，那我到底是用第二个任务的输入作为计算输入，还是用第一次任务S2产生的结果作为计算输入呢？” 这里就产生了冲突矛盾。

疑惑2：那我们要怎样规避冲突？

现在我们知道了非线性流水线会产生冲突了，那到底需要怎样规避冲突呢？
我们继续思考，冲突发生在什么地方？

答案是因为第一次的任务还没有完全计算完，更细节来说是在S1这个部件计算冲突。
解决这个问题，我们就需要把两次冲突的计算时间错开来。

有人会说：让第一次任务完全计算完才放行第二个任务的，这样可以吗？

这样太婆妈了，已经失去了流水线并行处理的意义了，变成顺序处理了，否决。

我们可以发现，其实不一定完全处理完第一次任务，只要两次冲突的计算不在一起即可，我们需要“不在一起”这个事情量化计算，可以选择用 “时间间隔” 的多少来作为计算单位。

所以，解决冲突本质上就是一个计算时间间隔的问题。

疑惑3：怎样求出禁止启动周期？

在开始讲调度之前，我们需要先理解两个概念，第一个叫 “启动周期”，意思是输入两个任务之间的时间间隔，另外一个叫 “禁止启动周期”，意思是当启动一个任务之后在禁止启动周期的时间点输入新的任务就会发生冲突。

如果要满足我们规避冲突的需求，你觉得我更需要知道 “启动周期” 还是 “禁止启动周期” ？

当然是 “ 禁止启动周期” 啦！

你想，如果我们知道了当启动一个任务之后再输入新的任务就会发生冲突的时间点，我们避开这些时间点，不就完成任务了！？

问题是，怎样去求出 “禁止启动周期” 呢？
我们先看一个叫 预约表 的东西。预约表 可以表达出 和 时空图一样多的信息。你看下面就知道了。

那为啥我们不用时空图分析非线性流水线呢？

首先，时空图不大方便表达有反馈回路的流水线，所以我们用预约表来表达非线性流水线，但预约表是可以表达线性流水线的，另外预约表还有一个超强的功能，利用表格可以转化为二进制位化成逻辑运算问题，在计组的很多问题里面，使用二进制标位可以简化理解很多复杂问题。

知道了预约表之后，我们就要找冲突的时间间隔到底发生在哪里了，先看S1，运算事件发生在时间点1和时间点9，差值是8，也就说一旦任务启动，在8个时间间隔之后你偏要在这个点输入第二任务就会发生冲突。

那好，我们依样画葫芦对S2，S3，S4，S5计算差值，不难找出，第一行（S1）有差值8，第二行（S2）有差值：1，5，6，第三行没有（因为只有一次发生），第四行和第五行都只有一个：1。

这里讲一下第二行的1，5，6是怎样计算出来的：
首先找出时间点：2，3，8，<2和3的差值：1>，<2和8的差值：6>，<3和8的差值：5>

综合以上所有行（段）的差值，去重，之后得到一个数集F={1,5,6,8}

我们管像F这样的数集叫做“禁止表”

但数集不适合我们进行逻辑思考，我们转化为更加直观的二进制的标签;
F={1,5,6,8}→C0=10110001F=\{1,5,6,8\}\rightarrow C_0=10110001F={1,5,6,8}→C0​=10110001

不懂？解释就是：$1^{8}01^6{1}^{5}001^1$，这该懂了吧，按位置看就行。

我们管像$C_0$这样的二进制数叫冲突向量

由于这是我们一开始在预约表得出来的，所以叫做“初始冲突向量”

到这里我们捋一下，我们是怎样得到 这个“初始冲突向量”的。

预约表$\Rightarrow$逐行求逐元素差值$\Rightarrow$禁止表$\Rightarrow$二进制位元化$\Rightarrow$初始冲突向量

至此，我们得到了我们的禁止启动周期的集合：禁止表，我们还进一步得到了冲突向量。

疑惑4：找出初始的禁止启动周期，冲突就解决了吗？

哈哈，还没呢！！！！

你是否忘记考虑这样一件事情，当第一个任务没有计算完的时候，你输入第二个任务，那第二个任务是否和第三个任务冲突呢，第三个和第四个呢？？？？嘿，是不是有点想撞墙了

但是在掌握了解决第一次和第二次任务的经验之后，我们至少有这样的情报：禁止启动周期是可以被枚举出来的，而且进一步分析，禁止启动周期的变化可以被逻辑计算出来的，实际上，我们分析完第一次和第二次之后，第一次的禁止启动周期就不是我们考虑的重点了，第二次的禁止启动周期变成了我们关注的事情，现在有没有发现有种证明归纳法的味道了？

我们想一下，新的冲突是怎样产生的？

答案是第二次的计算占用了新的时间点，我们假设第二任务和第一个任务相隔了 $j$ 个时间周期，当第二个任务进入流水线的时候，第一个任务已经在流水线前进了 $j$ 个时间周期，那么初始的禁止表里面的间隔对于第二任务而言就是偏移了 $j$ 个周期而已，我们对冲突向量右移 $j$ 位即可。

这样还不够，我们还需要和初始冲突变量做一次或运算来去重。

这样我们就得到了产生新的冲突向量的公式：
$$new{C}_0=sh{r}^j(C_0)\vee C_0$$

举个例子，之前我们拿到了一个初始冲突向量：$C_0=10110001$，根据这个冲突向量给出的情报，我们能在第一个任务启动之后的2，3，4，7个周期之后进入，其他都不行。

我们分情况考虑，假如在2个周期之后进入，那么执行产生新的冲突向量公式就是对$C_0$算术右移2位之后做或运算，$00101100\vee 10110001=10111101$，接下来对3，4，7依样画葫芦即可。

• 第一次启动之后2个周期之后进入$\Rightarrow$新的冲突向量$(10111101)$
• 第一次启动之后3个周期之后进入$\Rightarrow$新的冲突向量$(10110111)$
• 第一次启动之后4个周期之后进入$\Rightarrow$新的冲突向量$(10111011)$
• 第一次启动之后7个周期之后进入$\Rightarrow$新的冲突向量$(10111001)$

对于所有的情况，我们做类似的操作，就可以得到一个流水线状态机，如下图：

需要注意的是，我们所有的状态最后都要回到初始状态，这就是$9^{+}$的含义。

出现了状态机，至此，我们已经有能力规避所有的冲突了。

为什么？！还问为什么，状态都被你枚举出来了，还能怎样冲突，你已经掌握了所有可能不发生冲突的走法了。

从初始状态出发，任何一个闭合回路都可以看成一种调度方案，比如(2,7)，我们反复循环使用2和7这两个启动周期即可规避所有的冲突。

最优调度方法的选择

我们进一步思考，到底哪一种调度方案更好呢？我们需要使用延迟时间来判断，因为我们当然希望接近不间断地并发处理任务，延迟时间我们只需要计算启动周期的平均值即可。

如下表：

如图所示，延迟最小的就是最优的调度策略，（3，4）策略荣获此名。

但（3，4）策略是不等间隔的策略，不等间隔会给计算机控制变得更复杂，我们在实际应用中更偏向于等间隔的调度策略。

推理总结：

至此，所有的单功能流水线调度问题解释完毕，我们来捋一下逻辑。

首先，我们讨论了为什么流水线产生冲突的原因，分析出我们需要计算禁止启动周期，然后利用预约表计算出 禁止表（禁止启动周期集），然后计算出初始冲突向量，推理归纳，得出冲突向量的变化公式，计算出所有的状态（所有的冲突向量），画出了状态机，最后计算启动周期的平均值得出延迟周期，分析出最优的流水线调度策略。

如果给一个方便记忆的：题目一般会先给出预约表的
预约表$\to$禁止表$\to$初始冲突向量$\to$所有的冲突向量$\to$状态机$\to$最优调度策略

流水线的相关和冲突

指令执行分为五个步骤，IF，ID，EX，MEM，WB，（取址，译码，执行，访存，写回）

相关
指的是两条指令之间存在依赖关系，分为：数据相关，名相关，控制相关。

• 数据相关：后面的指令需要用到前面指令的计算结果
• 名相关：两条指令用到了同一个寄存器，但是两条指令之间没有数据流动。细分为：反相关和输出相关。反相关的意思是：前面的指令读了，后面的指令写了，对于同一个寄存器；输出相关的意思是：前面的指令写了，后面的指令也写了，对于同一个寄存器。
• 控制相关：分支指令引发的，与分支情况相关不能把某些指令变更位置的。

冲突

• 结构冲突：常说的独占某个硬件部件问题，比如对同一个寄存器，一个指令准备读，一个准备写。
• 数据冲突：数据相关和名相关所导致的问题。
• 控制冲突：遇到分支指令或者其他改变PC寄存器的指令所引发的冲突。

对于数据冲突分为以下几类：

• RAW（读之前就写了）
• WAW（写之前就写了）
• WAR（写之前就读了）

5. 解决流水线的冲突

解决结构冲突
这是由于硬件资源不足所引起的，
方法【1】：“气泡”，或者叫 “停顿” （STALL）

可以去除掉指令i+3和Load指令对于Mem的使用冲突。但由于结构冲突是常见频繁的，不能这样经常停顿会大幅度影响性能。
方法【2】：采用多个独立的存储器，专门针对指令的存储器和数据的存储器，还有采用多个分离的Cache，数据Cache和指令Cache

解决数据冲突
方法【1】：使用定向技术（旁路）来解决，就是在计算结果还没完全出来之前就通过硬件把结果传到下面需要的部件。没完全出来的意思是，整条指令完整的执行了（五个步骤），但实际上，我们在EX阶段之后，在ALU的输出就能拿到结果了，这个时候就通过一条特定的数据通路把数据传到下面需要的部件。例子如下：：

使用旁路进行解决：

方法【2】使用编译器优化的方法，我们利用编译器重新组织指令顺序来消除冲突，我们叫这种技术做指令调度和流水线调度。思想在之前讲流水线调度的地方。

解决控制冲突
最简单的办法是遇到分支指令就暂停下面的任务，等所有的指令排空之后再继续。但这是一种极度浪费时间的做法。

我们可以考虑使用 “延迟槽” 使流水线继续运行下去，延迟槽的指令是空的，不作为的。凑够流水线的形状。