二分类问题
我们所说的逻辑回归问题实际上是分类问题的一种，并不是回归问题，这是历史遗留原因
y
∈
y\in
y∈ {0,1}
Negative class 和Positive class
为什么线性分类器在分类问题表现不好？
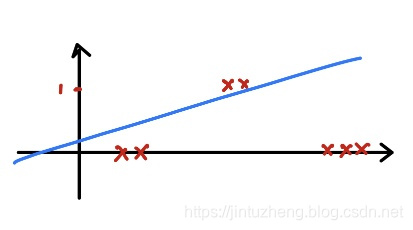
引入逻辑回归模型
我们需要满足：
0
≤
h
(
θ
)
≤
1
0 \leq h(\theta)\leq1
0≤h(θ)≤1
而我们之前设置的回归假设函数：
Z
=
θ
X
Z=\theta X
Z=θX
引入一个特别的函数模型：Sigmoid 函数模型：
G
(
z
)
=
1
1
+
e
−
z
G(z)=\frac{1}{1+e^{-z}}
G(z)=1+e−z1
图像：
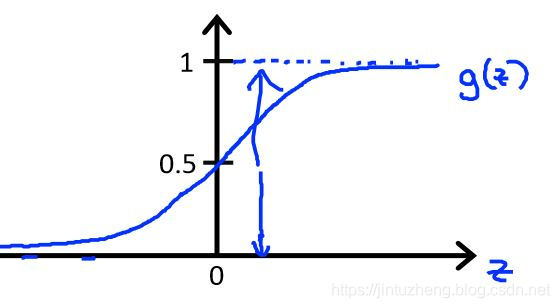
这样就能满足
0
≤
h
(
θ
)
≤
1
0 \leq h(\theta)\leq1
0≤h(θ)≤1 了。
分类问题的损失函数
由于我们所使用的Sigmoid函数是非线性函数，假如使用我们之前的那个损失函数会导致出现多个局部谷点，难以收敛，我们必须为其重新设计一个。根据统计学的极大似然统计得到有一个函数
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
l
o
g
(
1
−
h
θ
(
x
)
)
Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))
Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
因为我们的 y 只有两种值，要不就是0 和 1。
实际上这个函数可以分为：
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
if
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
if
y
=
0
Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x)) & \text{if } y=1 \\ -log(1-h_\theta(x)) & \text{if } y=0 \end{cases}
Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))if y=1if y=0
示例：当 y=1 的图像
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
l
o
g
(
h
θ
(
x
)
)
Cost(h_\theta(x),y)=-log(h_\theta(x))
Cost(hθ(x),y)=−log(hθ(x))
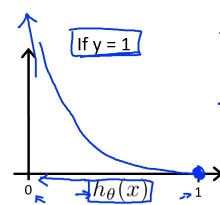
一旦误判足够严重，惩罚会非常大。
h
θ
(
x
)
→
0
,
C
o
s
t
→
+
∞
h_\theta(x)\rightarrow0,Cost\rightarrow+\infty
hθ(x)→0,Cost→+∞
梯度下降算法外的高级优化器
我们之前学习到的梯度下降算法都是我们手动选择学习率，但像：
- Conjugate gradient
- BFGS
- L_BFGS
这些算法无需手动选择学习率，使用这些高级算法进行优化将会收敛更快。不要自己手动尝试去实践这些算法。
多分类问题
我们只需要把多分类问题转化成多个二分类问题即可，比如我们需要分出3类，那么我们将使用3个二分类器。
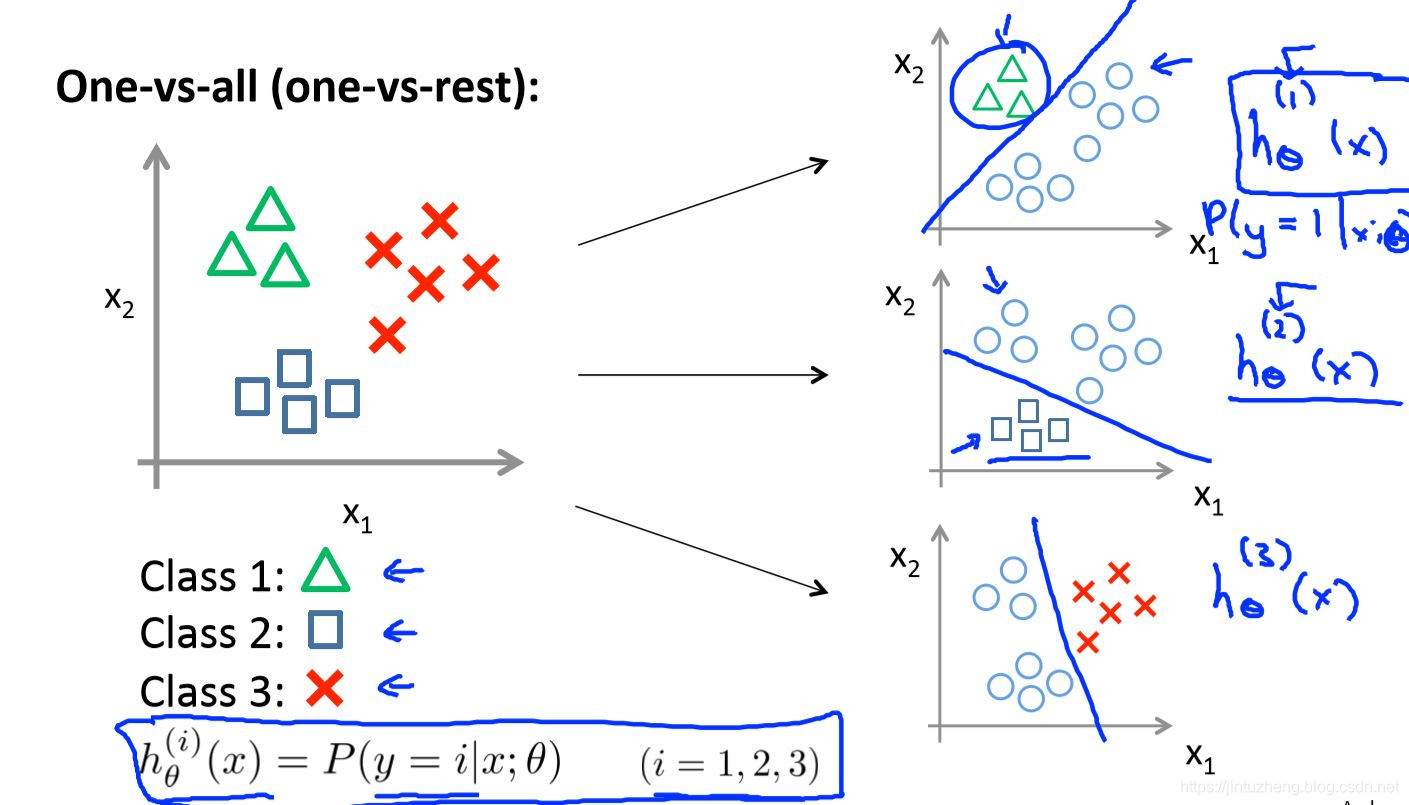
输入
X
i
n
p
u
t
X_{input}
Xinput ，只需要选择
max
i
h
θ
i
(
X
)
\max_{i}h^{i}_\theta(X)
maxihθi(X) 作为预测输出即可。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
