LeetCode hot 100—接雨水

原创于 2025-03-22 11:14:21 发布 · 561 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展 #c++ #数据结构

leetcode 专栏收录该内容

87 篇文章

订阅专栏

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

分析

每个位置i能接住的雨水量由其左右两侧的最大高度决定，公式为：

water[i] = min(leftMax[i], rightMax[i]) - height[i]

其中leftMax[i]是位置i左侧最高柱子的高度，rightMax[i]是右侧最高柱子的高度。

双指针法

双指针法的核心思想是通过维护两个指针 left 和 right 分别从数组的两端向中间移动，同时维护两个变量 leftMax 和 rightMax 分别记录从左到右和从右到左的最大高度。根据当前指针所指位置的高度与最大高度的关系来计算该位置能接住的雨水量。

时间复杂度：O( $n$ )， $n$ 是数组的长度

空间复杂度：O(1)

class Solution {
public:
    int trap(std::vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int leftMax = 0, rightMax = 0;
        int ans = 0;
        while (left < right) {
            if (height[left] < height[right]) {
                if (height[left] >= leftMax) {
                    leftMax = height[left];
                } else {
                    ans += leftMax - height[left];
                }
                left++;
            } else {
                if (height[right] >= rightMax) {
                    rightMax = height[right];
                } else {
                    ans += rightMax - height[right];
                }
                right--;
            }
        }
        return ans;
    }
};

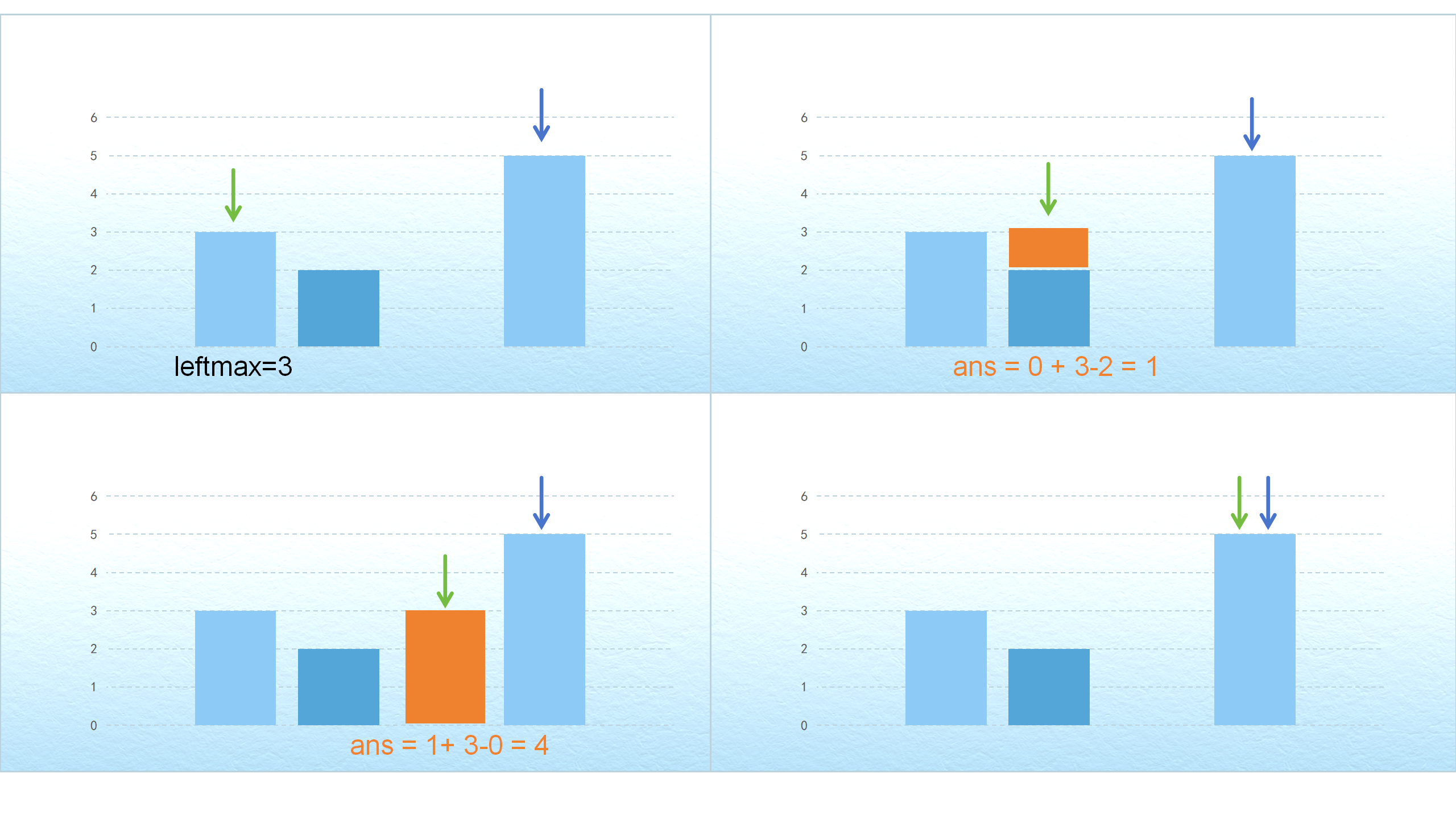
[3,2,0,5] 为例图示

单调栈法

单调栈法的核心思想是维护一个单调递减的栈，当遇到比栈顶元素高的柱子时，说明可以形成一个低洼区域，此时可以计算该区域能接住的雨水量。

时间复杂度：O( $n$ )， $n$ 是数组的长度

空间复杂度：O( $n$ )

class Solution {
public:
    int trap(std::vector<int>& height) {
        std::stack<int> st;
        int ans = 0;
        for (int i = 0; i < height.size(); ++i) {
            while (!st.empty() && height[i] > height[st.top()]) {
                int top = st.top();
                st.pop();
                if (st.empty()) {
                    break;
                }
                int left = st.top();
                int width = i - left - 1;
                int h = std::min(height[left], height[i]) - height[top];
                ans += width * h;
            }
            st.push(i);
        }
        return ans;
    }
};