题目
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例
示例 1:
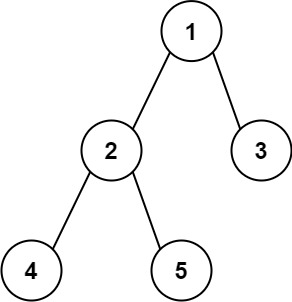
输入:root = [1,2,3,4,5] 输出:3 解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。示例 2:
输入:root = [1,2] 输出:1
分析
理解二叉树直径的本质:它是树中任意两个节点之间最长路径的边数。而任意一条路径都可以看作是由某个节点为根,其左子树的深度加上右子树的深度。
深度优先搜索
递归计算以每个节点为根的树的深度来实现。在递归函数中,先判断节点是否为空,为空则深度为 0;否则递归计算左右子树深度,更新最大直径(即左右子树深度之和),并返回当前节点为根的树的深度(左右子树深度最大值加 1)。最后从根节点开始调用该递归函数,完成计算后返回最大直径。
时间复杂度:O(),
为二叉树节点的个数
空间复杂度:O(),
表示二叉树的高度
class Solution {
private:
int maxDiameter = 0;
// 计算以当前节点为根的树的深度,同时更新最大直径
int depth(TreeNode* node) {
if (node == nullptr) {
return 0;
}
// 递归计算左子树的深度
int leftDepth = depth(node->left);
// 递归计算右子树的深度
int rightDepth = depth(node->right);
// 更新最大直径,直径为左子树深度 + 右子树深度
maxDiameter = std::max(maxDiameter, leftDepth + rightDepth);
// 返回当前节点为根的树的深度,深度为左右子树深度的最大值加 1
return std::max(leftDepth, rightDepth) + 1;
}
public:
int diameterOfBinaryTree(TreeNode* root) {
depth(root);
return maxDiameter;
}
};






















 679
679

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










