LeetCode hot 100—翻转二叉树

rigidwill666

于 2025-03-07 11:10:41 发布

阅读量160

点赞数 4

CC 4.0 BY-SA版权

分类专栏： leetcode 文章标签： leetcode 算法数据结构

本文链接：https://blog.youkuaiyun.com/rigidwill/article/details/146089510

leetcode 专栏收录该内容

87 篇文章

订阅专栏

题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例

示例 1：

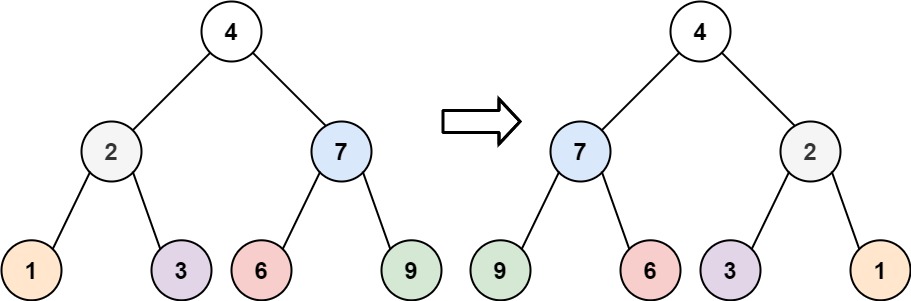
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

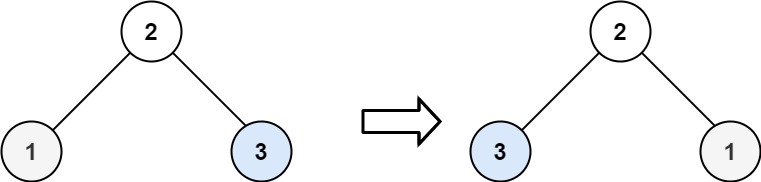
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

分析

递归法

先递归地翻转左子树和右子树，然后交换当前节点的左右子树。

时间复杂度：O( $n$ )， $n$ 是二叉树中的节点数

空间复杂度：O( $h$ )， $h$ 是二叉树的高度。最坏情况下二叉树退化为链表，空间复杂度为 O( $n$ )；平均情况下空间复杂度为 O( $\log n$ )

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        // 递归翻转左子树
        TreeNode* left = invertTree(root->left);
        // 递归翻转右子树
        TreeNode* right = invertTree(root->right);
        // 交换当前节点的左右子树
        root->left = right;
        root->right = left;
        return root;
    }
};

迭代法

使用队列来实现广度优先搜索（BFS）。遍历队列中的每个节点，交换其左右子树，并将其左右子节点加入队列。

时间复杂度：O( $n$ )， $n$ 是二叉树中的节点数

空间复杂度：O( $m$ )， $m$ 是二叉树中节点数最多的那一层的节点数

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        std::queue<TreeNode*> nodeQueue;
        nodeQueue.push(root);
        while (!nodeQueue.empty()) {
            TreeNode* current = nodeQueue.front();
            nodeQueue.pop();
            // 交换当前节点的左右子树
            TreeNode* temp = current->left;
            current->left = current->right;
            current->right = temp;
            // 如果左子节点不为空，将其加入队列
            if (current->left) {
                nodeQueue.push(current->left);
            }
            // 如果右子节点不为空，将其加入队列
            if (current->right) {
                nodeQueue.push(current->right);
            }
        }
        return root;
    }
};