本文首发于 算法社区,转载请注明出处,谢谢。
名称#
Savitsky-Golay平滑算法
作用#
信号平滑处理可以除去高频噪音对数据信号的干扰,是消除噪音最常用的一种方法
算法原理#
通过多项式对移动窗口内的数据进行多项式最小二乘拟合,算出窗口内中心点关于其周围点的加权平均和。
计算公式: (3-1)
(3-1)
式(3-1)中的 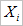 和
和 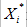 为平滑前、后的数据,
为平滑前、后的数据, 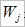 是移动窗口平滑中的权重因子(窗口长度 2r + 1)。
是移动窗口平滑中的权重因子(窗口长度 2r + 1)。
窗口移动多项式拟合的基本思想是:利用多项式对窗口内 N = 2r + 1 的波谱点进行多项式最小二乘拟合,将窗口内等距离的数据拟合成 k 次多项式: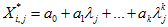 ,
, 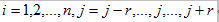
其中 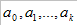 为待定系数或权重。
为待定系数或权重。
实例#
以窗口为5的二次多项式为例进行拟合。
设有5个数据对(等间隔): 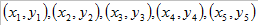 ,进行二次多项式拟合:
,进行二次多项式拟合: 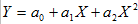
应用最小二乘法,使误差 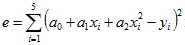 达到最小,所以分别对
达到最小,所以分别对 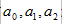 进行求导
进行求导 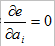 ,得:
,得: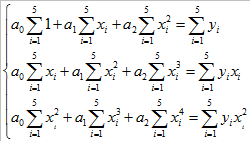 (4-1)
(4-1)
由于等间隔,所以 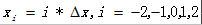 ,式(4-1)可化为
,式(4-1)可化为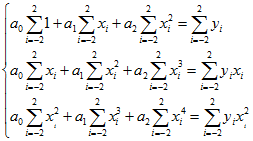 (4-2)
(4-2)
注意式(4-2)下标的改变
而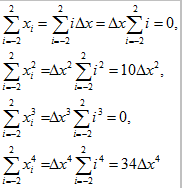 (4-3)
(4-3)
由式(4-2)和式(4-3)即可求得: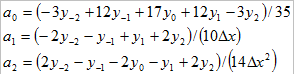 (4-4)
(4-4)
对于中心点,也即所求的平滑点,其值为: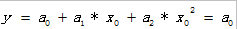 ,
,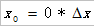
由式(4-4)知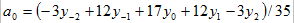 ,
,
故权重为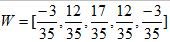 ,即可利用权重对中心点进行平滑
,即可利用权重对中心点进行平滑
本文首发于 算法社区 dspstack.com,转载请注明出处,谢谢。







 本文深入探讨了Savitsky-Golay平滑算法,这是一种常用的信号处理方法,用于去除高频噪音。文章详细介绍了算法原理,通过多项式最小二乘拟合移动窗口内的数据,实现对中心点的加权平均和平滑处理。
本文深入探讨了Savitsky-Golay平滑算法,这是一种常用的信号处理方法,用于去除高频噪音。文章详细介绍了算法原理,通过多项式最小二乘拟合移动窗口内的数据,实现对中心点的加权平均和平滑处理。
















 1万+
1万+










