初步条件
1.假设数据位有7位,为 101001
D(初始) = 101001
2.假设给定约定多项式为4位,为1100,可求得阶级r为len(1100) - 1 = 4-1 = 3
P(多项式) = 1100
r = len(P) -1 = 4-1 = 3
3.根据流程,计算过程中的数据位需要在末尾加上 第二步所求的阶级数数量的阿拉伯数字0,也是是加上三个0。
D(计算中的数据位) = 101001000
计算过程
那么可以写出计算式初始稿如下:
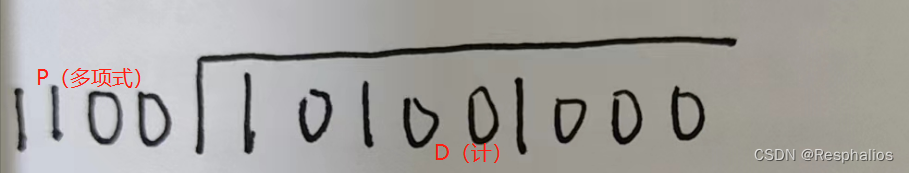
我们先求第一位商,多项式有四位,我们就在D(计)的第四位上置放1
(区别一.与普通除法的除不尽第一位为0不同,第len(P)位无条件放置1)
然后像普通除法一样把除数沉下去,这一步在计算冗余码中是固定不变的,不受任何因素的影响,如图:

接下来就是冗余码除法计算中区别于普通除法的第二个地方
(区别二:普通除法的单过程取模是直接相减,但是在这里需要使用模2除,可以简单的理解为两两进行独立异或计算且不存在进位):
演示
a:1010
b:1100
c:待求
这两数进行模2除的求解过程
a为取模过程中的上位数,b为下位数 c为所求结果
a[0] = 1, b[0] = 1 那么c[0]的结果为这两数的异或计算(相同为0不同为1) ,1异或1等于0,所以c[0] = 0
a[1] = 0, b[1] = 1,所以c[1] = 1
a[2] = 1, b[2] = 0,所以c[2] = 1
a[3] = 0, b[3] = 0,所以c[3] = 0
故 c = 0110
如下:
 发现 这一步的模运算结果为0110,前置的0我们需要进行忽略,那么实际上只有3位的110剩余,而3位不足以被四位的1100所除,这里可以像普通除法一样从上面拉下来一个数字
发现 这一步的模运算结果为0110,前置的0我们需要进行忽略,那么实际上只有3位的110剩余,而3位不足以被四位的1100所除,这里可以像普通除法一样从上面拉下来一个数字

发现满足要求可以继续除,那么继续在商处放置一个1(什么时候放0后面会讲到),且将1*1100的结果1100放置于平齐最后一步的的一个有效数字下:

在进行异或计算,直到上面的商没位置即运算完成

最后的结果0100即使我们所求的FCS余数:





















 2992
2992

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








