python内置库——heapq（实现小顶堆）

官网地址：
heapq — 堆队列算法

特点

堆本身还是一个树结构，通常还是使用数组进行存储，方便操作。
我们找到py有一个基本语法是数组下标从零开始，py中的堆也是这样实现的，问题就是使得父子关系不那么直观。

C++中的堆是大顶堆（大根堆），一般也是常用的一种堆，但是py中还是选择了实现一个小顶堆。

内置方法

1. 创建堆：
   如果是用过counter的，可能感觉上是差不多的，就是对一个可迭代序列调用方法即可
   heapify(iterable)
   不过官方文档上的介绍，这个实现是原地的，并且是在线性时间内调整成堆。
2. 弹出根元素（最小值）
   heappop(heap)，返回最小值。当堆为空，报错indexerror
3. 压入元素
   heappush(heap,item)
4. 压入&弹出
   这部分有两个函数，分别是heappushpop(heap,item)和heapreplace(heap,item)
   其中pushpop函数是先push，再pop，replace函数是先pop，再push
   区别就是，当你压入的元素比根节点要小，那么两个的返回值是不一样的。
   当然，给出这两个函数的原因也很简单，要比分开调用的效率更高，当然使用也更方便

这还不算完，heap库还提供了一些和堆排序相关的通用函数。

1. merge(*iterables, key=None, reverse=False)
   实现将多个可迭代序列根据堆排序合并成一个可迭代序列（输入、输出都要求是已排序）
   其中的key和reverse和sort方法之类都差不多，不做赘述，这部分是在3.5版本中加入。
2. nlargest(n, iterable, key=None)
   从可迭代序列iterable中提取出前n个最大的元素，组成列表返回。
3. nsmallest函数，和上面基本相同，返回最小的n个。

在官方文档的介绍中，最后的两个函数(nlargest和nsmallest函数）在n比较小的情况下合适，太大了建议使用sorted，如果是n=1，直接max/min不香吗。

举例

import heapq
from icecream import ic
def heapsort(iterable):
    '''将列表中的每一个元素压入堆（其实就是个列表），最后弹出'''
    h = []
    for value in iterable:
        heapq.heappush(h,value)
    return [heapq.heappop(h) for _ in range(len(h))]

print(heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0]))
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

def heapsort2(iterable):
    '''这个案例是突出本地排序，而不是像counter那样存储到一个类的实例中'''
    heapq.heapify(iterable)
    return iterable

print(heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0]))
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

# 其他方法的介绍，这部分有一点就是他内部是一个树结构，感兴趣的自己草纸上画一下，看看有没有问题
h = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
heapq.heapify(h)
ic(h)

heapq.heappush(h, 10)
ic(h)

ic(heapq.heappop(h))
ic(h)

heapq.heappushpop(h, 15)
ic(h)

heapq.heapreplace(h, 16)
ic(h)

# 这不看一下push一个更小值两个函数的区别
ic(heapq.heappushpop(h, -1))
ic(heapq.heapreplace(h, -2))
ic(h)

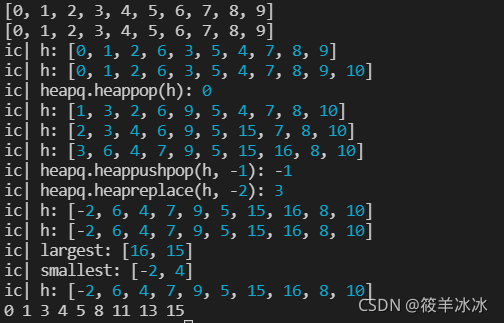
'''这部分的结果:
ic| h: [0, 1, 2, 6, 3, 5, 4, 7, 8, 9]
ic| h: [0, 1, 2, 6, 3, 5, 4, 7, 8, 9, 10]
ic| heapq.heappop(h): 0
ic| h: [1, 3, 2, 6, 9, 5, 4, 7, 8, 10]
ic| h: [2, 3, 4, 6, 9, 5, 15, 7, 8, 10]
ic| h: [3, 6, 4, 7, 9, 5, 15, 16, 8, 10]
ic| heapq.heappushpop(h, -1): -1
ic| heapq.heapreplace(h, -2): 3
ic| h: [-2, 6, 4, 7, 9, 5, 15, 16, 8, 10]'''

# 通用函数的介绍
a = [1,3,5]
b = [0,4,8]
c = [11,13,15]
x = heapq.merge(a,b,c)
for i in x:
    print(i,end=' ')
# 0 1 3 4 5 8 11 13 15

ic(h)
largest = heapq.nlargest(2, h)
ic(largest)
smallest = heapq.nsmallest(2,h)
ic(smallest)
ic(h)
'''这部分的结果
ic| h: [-2, 6, 4, 7, 9, 5, 15, 16, 8, 10]
ic| largest: [16, 15]
ic| smallest: [-2, 4]
ic| h: [-2, 6, 4, 7, 9, 5, 15, 16, 8, 10]
对h有影响'''