分治算法举例——最大&最小值问题、大数乘法和棋盘规划

在之前的博客中给出了递归方程的含义，以及时间复杂度的计算方式，
那么接下来给出一些典型的分治算法。

寻找最大值和最小值问题

给一个算法，寻找一个数组的最小值和最大值。（啥？这东西不是有手就行吗）
emm，我这个不一样啊，我这个是O(1.5n)的时间复杂度的。

方法一

还记得快排里面的将一个数组划分成两个数组，保证大的在后小的在前吧，我们就是采用这样的方式，不过没有那么复杂。
O(0.5n)：将数组折半，最后一个和第一个比较、倒数第二个和第二个比较……将小的放在前半段，大的在后半段。
O(n)：遍历两个小数组，分别对应寻找最大值和最小值

有人可能会想到，既然使用一次降低了时间复杂度，那么我多使用几次？
那我们就来讨论一下：每一次的折半，代价就是

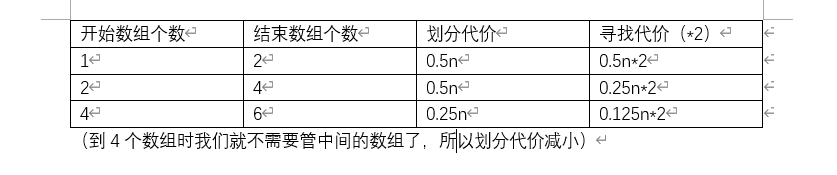
确实，当划分的规模越细，寻找的代价一定减小，但是表格中的代价是一步的代价，我们要做的是将之前所有的加起来，才能得到最终结果。
至少对前三项来说，代价都是1.5n没有改变，在整理了整个式子后我们发现代价一直都是1.5n，也就是实际上划分一次的代价和n次的代价是相同的。

伪代码：

Max-min(A)
Input:   数组A[1,…,n]
Output:数组A[1,…,n]中的max和min
For  i=1  To  n/2  Do
       IF  A[i] > A[n-i+1] THEN   swap(A