二叉树的应用——二叉排序树、选择树、判定树

选择树

这就要提到外部排序了。因为内存的空间不足，有时候不能将排序的全部内容都放在内存中完成，就像是新学期老师按身高排座位，教室内站不开就要到外面排队。
但计算机还有一些附加条件，比如外面空间有限，所以排身高只能在室内进行，所以呢，人们就将外存中的数据分为几组，在内存中排好了然后合并。

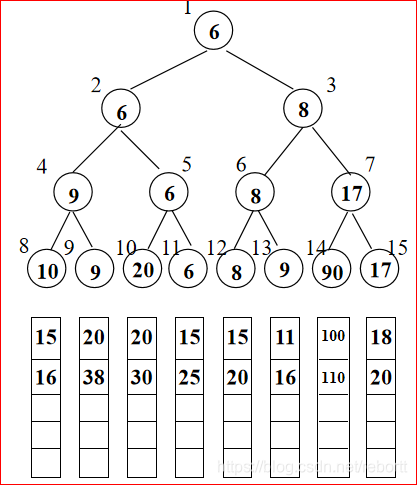
这个时候，选择树就登场了。图中一共是八组已经排好了的，每一组取最小的元素，然后按照满二叉树的结构排出最小的，（这里是第四组的6最小）所以第四组的15跟进，和剩下的7个数字接着比较。

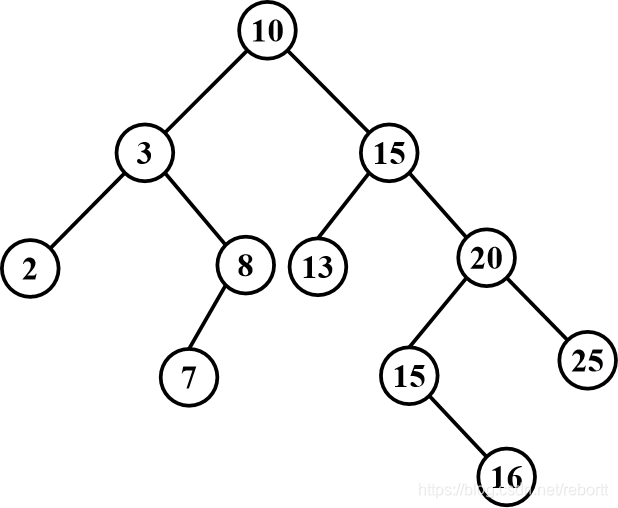
二叉排序树

如果不是空树，那么左子树的值小于根节点小于右子树，并且每一个子树都是二叉排序树
又叫二叉查找树，因为查找的效率要比线性查找更高。

由于其性质，所以只需要将树中序遍历，就能得到一个排好序的数列。

Struct  BST
{
	int data ;
	struct BST *lchild, *rchild ;
}

查找：思路很清晰，看一下就行

BST* search(int k, BST* F)
{   
	p = F;
    if ( p == Null )  
    	return Null ;
    else if ( k == p->data )
    	return p ;
    else if ( K < p->data )
    	return search( k,  p->lchild ) ;
     else if ( K > =p->data )
     	return search( k,  p->rchild ) ;
}

插入：

Void  Insert(int R , BST *F)
{  
	if (F == Null)
    {  
    	F = new BST;
        F->data = R ;
        F->lchild = Null ;
        F->rchild = Null ;   
    }
    else if( R.key < F->data )
    	Insert ( R , F->lchild )
    else if( R.key >= F->data )
        Insert ( R , F->rchild )
}

要知道，插入后的结点都是在叶子节点上，因为不停的比较直到到了某一个叶子节点才能确定是这个结点的哪边孩子。

删除：

void deleted(int data, BST* F)
{
	if(F)
	{
		if(data < F->data)
			deleted(data, F->lchild)
		else if(k > F->data)
			deleted(data, F->rchild)
		else
		{
			if(F->rchild == NULL)
				F = F->lchild;
			else if(F->lchild == NULL)
				F = F->rchild;
			else 
				F->data = DeleteMin(F->rchild);
		}
	}
}

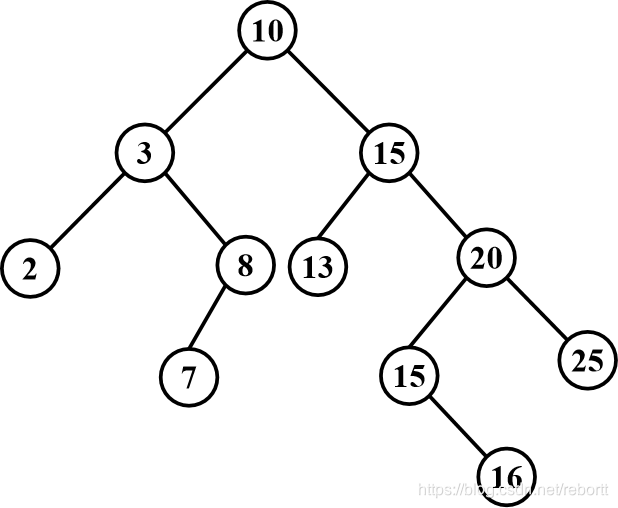
如果度数不为2，直接把一个孩子提上来就行了，叶子就直接为空；
但如果是2度结点，那么就需要找一个合适的结点代替了，下面就是DeleteMin函数求右孩子最左结点
（其实左孩子最右结点也行的）

int DeleteMin(BST* F)
{
	int ret;
	BST* p = F;
	if(!F->lchild)
	{
		ret = F->data;
		F = F->rchild;
		free(p);
		return ret;
	}
	else 
		return DeleteMin(F->lchild);
}

判定树

和选择树差不多，就是用到了树的结构：
八枚硬币，有一个是假的，比较三次确定哪个是假币以及假币和真币相比质量如何？

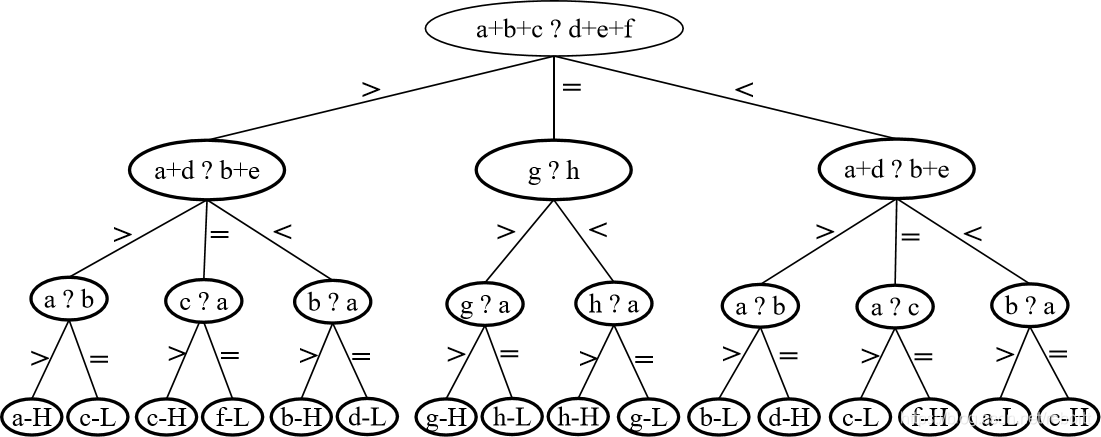
特点：

• 判定树整体是该问题的所有可能解；
• 每一个从根到叶子都是一种可能解
• 每一个非叶子节点对应的子树都是不同的可能性
  最后贴一张图，互相伤害，反正我是没做出来几个，要是大佬们有思路了留言哈