线段树的原理与模板（上）

昨天训练第一次做到了线段树的题，琢磨了两个小时代码，大概看懂了，今天特地来整理总结记录一下原理与模板
昨天看的一篇很不错的博文，也推荐给大家：https://blog.youkuaiyun.com/iwts_24/article/details/81484561
下面都是自己语言描述整理的

首先
为什么要使用线段树？
假设医院有8种药，每次开药进药都会引起响应库存数量的变化，也需要记录方便管理，我们都会想到用数组去存储

int a[8]={1,2,3,4,5,6,7,8};

如果进药（比如都是八盒），那就是很常规的O(n)遍历循环

for(int i=0;i<8;i++)
{
	a[i]+=8;
}

然后要求[a,b]的和，也当然是遍历，O(b-a)

线性的时间复杂度还是不太好的如果在比赛中，m个数据n个操作，可能会有t的可能
所以，使用线段树这种数据结构来存储和操作数据，降低时间复杂度

什么是线段树？
一种完全二叉树，除了最下层和次下层，其余层都放满，一定条件下会成为满二叉树，每个节点代表一个区间一种范围，树根节点代表最大的区间1-n，在医院这个例子中就是[1,8]
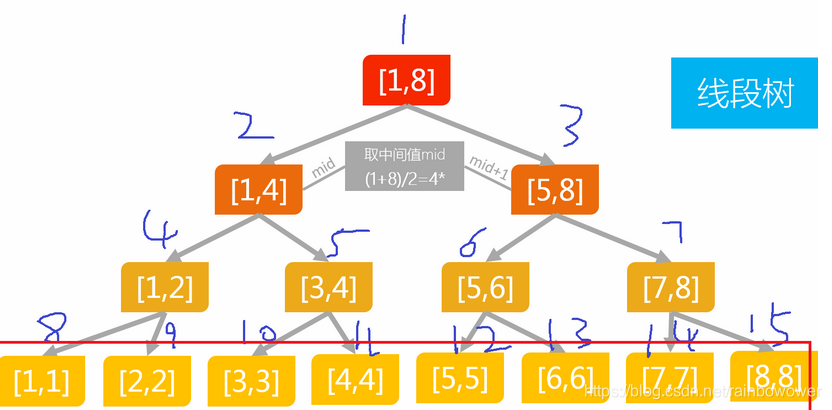树根节点，代表a[1-8]的和

接下来就是代码部分了，一段一段剖析着记录吧

线段树的操作-建树
大致的数据结构了解了，首先我们需要创建一个结构去存储，易看出线段树非常耗费空间，所以不管是结构体还是数组，都应该开大点空间，比如四倍

#define MAX 200000
 
int tree[4*MAX];
 
void init(){
    memset(tree,0,sizeof(tree));
}

建树开始

void build(int node,int l,int r){
	if(l == r){ // 到达叶子节点，赋值
		cin >> tree[node];
		return;
	}
	int mid = (l+r)/2;
	build(node*2,l,mid); // 进入子树开始递归
	build(node*2+1,mid+1,r);
	tree[node] = tree[node*2] + tree[node*2 + 1]; // 回溯
}

一开始调用为build(rt,1,8)进入函数（rt为树根节点），叶子节点赋值，通过二叉递归回溯给一系列父亲节点代入数据，创建好这棵树

线段树的操作-单点修改
单点操作比区间操作方便快捷的多，代码也简单，没有要用到lazy数组，单点更新很类似二分查找，二分递归找到更新点并更新，回溯后自然更新了上层一系列区间节点

// 单点更新，n为更新值，index为更新点，lr为更新范围
void update(int n,int index,int l,int r,int node){
	if(l == r) {
		tree[node] += n; // 更新方式，可以自由改动
		return;
	}
	int mid = (l+r) / 2;
	// push_down(node,mid-l+1,r-mid); 若既有点更新又有区间更新，需要这句话
	if(index <= mid){
		update(n,index,l,mid,node*2);
	}else{
		update(n,index,mid+1,r,node*2+1);
	}
	tree[node] = tree[node*2] + tree[node*2 + 1]; // 回溯过程，需要将线段树上层数据更新
}

和建树过程的回溯思想是一样的，很方便

懒惰标记
懒惰标记的作用呢，就是省去了改一次更新一次的繁琐，将修改的积累在一起，等到更新时统一更新线段树，理论上建一个跟线段树同样大小的数组，称为懒惰数组，表示每个节点的懒惰标记，有如下的操作：
1、修改数据的时候，每次递归到某节点，修改数据以后将数据的变化添加到数组中。
2、当使用到这个节点的时候，发现对应的懒惰标记存在，那就更新该节点，及以下所有的节点
简而言之就是不用时积累，使用时统一更新

那么懒惰数组的更新非常简单，对线段树更新的时候就可以添加到懒惰标记，但是在使用的时候，我们需要用一个函数来完成懒惰标记的下传操作，也就是更新积累的值。代码：

void push_down(int node,int l,int r){
	if(lz[node]){
		int mid = (l+r) / 2;
		lz[node*2] += lz[node];
		lz[node*2 + 1] += lz[node];
        // 注意线段树的数据更新方式要一致
		tree[node*2] += 1LL*(mid - l + 1)*lz[node];
		tree[node*2 + 1] += 1LL*(r - mid)*lz[node];
		lz[node] = 0;//lz标记清零
	}
}

当lz[rt]存在值时，我在使用这个节点，以下的节点就需要更新了，就利用二叉向下传递lz，同时也要更新数据，最终记得标记清零
注意，下推的时候不是一直更新到叶子节点，而是只更新当前节点以及2个子树，因为实际操作的时候，只要碰到对某节点的操作就要调用push_down()函数，所以每次只用下推一层即可。

线段树的操作-区间更新

单点更新类似二分查找，更新的时候对经过的路径进行操作就可以了。但是区间更新需要考虑整个区间。线段树除了叶子节点，都表示了一段区间的值，那么就要配合懒惰标记在整个区间上进行操作。先看代码：

// 区间更新，lr为更新范围，LR为线段树范围，add为更新值
void update_range(int node,int l,int r,int L,int R,int add){
	if(l <= L && r >= R){
		lz[node] += 1LL*add;
		tree[node] += 1LL*(R - L + 1)*add; // 更新方式
		return;
	}
	push_down(node,L,R);
	int mid = (L+R) / 2;
	if(mid >= l) update_range(node*2,l,r,L,mid,add);
	if(mid < r) update_range(node*2 + 1,l,r,mid+1,R,add);
	tree[node] = tree[node*2] + tree[node*2 + 1];
}

单点更新是自下而上更新，而区间更新可以看做自上而下，找到区间，配合懒惰标记更新下一层

线段树的操作-区间查找

区间查找和区间更新有一定的类似之处，值得注意的是，每次查询到点时一定要调用一次push_down更新值及下一层节点的lazy值

// 区间查找
LL query_range(int node,int L,int R,int l,int r){
	if(l <= L && r >= R) return tree[node];
	push_down(node,L,R);
	int mid = (L+R) / 2;
	LL sum = 0;
	if(mid >= l) sum += query_range(node*2,L,mid,l,r);
	if(mid < r) sum += query_range(node*2 + 1,mid+1,R,l,r);
	return sum;
}

理解懒惰数组及其模板后，确实有些胸有成竹，但具体到题目中的话，对模板进行修改就会增加难度，不易修改，所以要不要使用lazy数组得看具体情况而定，等下篇博客再记录.

接下来是整个模板，引用那篇博客里的模板，做个记录

#include<iostream>
#include<string>
#define LL long long
#define MAX 1001
 
using namespace std;
 
int tree[MAX]; // 线段树
int lz[MAX]; // 延迟标记
 
void init(){
	memset(tree,0,sizeof(tree));
	memset(lz,0,sizeof(lz));
}
 
// 创建线段树
void build(int node,int l,int r){
	if(l == r){
		cin >> tree[node];
		return;
	}
	int mid = (l+r)/2;
	build(node*2,l,mid);
	build(node*2+1,mid+1,r);
	tree[node] = tree[node*2] + tree[node*2 + 1];
}
 
// 单点更新，n为更新值，index为更新点，lr为更新范围
void update(int n,int index,int l,int r,int node){
	if(l == r) {
		tree[node] = n; // 更新方式，可以自由改动
		return;
	}
	int mid = (l+r) / 2;
	// push_down(node,mid-l+1,r-mid); 若既有点更新又有区间更新，需要这句话
	if(index <= mid){
		update(n,index,l,mid,node*2);
	}else{
		update(n,index,mid+1,r,node*2+1);
	}
	tree[node] = tree[node*2] + tree[node*2 + 1];
}
 
void push_down(int node,int l,int r){
	if(lz[node]){
		int mid = (l+r) / 2;
		lz[node*2] += lz[node];
		lz[node*2 + 1] += lz[node];
		tree[node*2] += 1LL*(mid - l + 1)*lz[node];
		tree[node*2 + 1] += 1LL*(r - mid)*lz[node];
		lz[node] = 0;
	}
}
 
// 区间更新，lr为更新范围，LR为线段树范围，add为更新值
void update_range(int node,int l,int r,int L,int R,int add){
	if(l <= L && r >= R){
		lz[node] += 1LL*add;
		tree[node] += 1LL*(R - L + 1)*add; // 更新方式
		return;
	}
	push_down(node,L,R);
	int mid = (L+R) / 2;
	if(mid >= l) update_range(node*2,l,r,L,mid,add);
	if(mid < r) update_range(node*2 + 1,l,r,mid+1,R,add);
	tree[node] = tree[node*2] + tree[node*2 + 1];
}
 
// 区间查找
LL query_range(int node,int L,int R,int l,int r){
	if(l <= L && r >= R) return tree[node];
	push_down(node,L,R);
	int mid = (L+R) / 2;
	LL sum = 0;
	if(mid >= l) sum += query_range(node*2,L,mid,l,r);
	if(mid < r) sum += query_range(node*2 + 1,mid+1,R,l,r);
	return sum;
}
 
int main() {
	init();
	build(1,1,8);
 
	system("pause");
	return 0;
}