点到链的距离
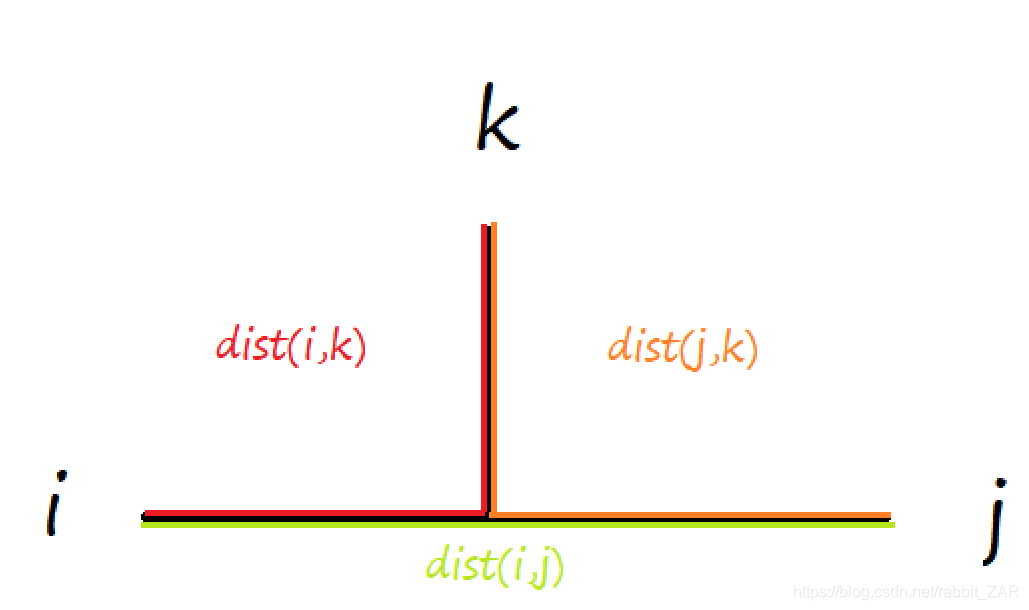
设点kkk,链的端点(i,j)( i , j )(i,j),点到链的距离为DDD。
定义d[i,j]d [ i , j ]d[i,j]表示点iii到点jjj的距离。
可得 D=d[i,k]+d[j,k]−d[i,j]2D=\frac{d[i,k]+d[j,k]-d[i,j]}{2}D=2d[i,k]+d[j,k]−d[i,j]
原理如图:
矩形的相交区域坐标

设黑色矩形左上角坐标 ( x1 , y1 ),右下角 ( x2 , y2 ) ;
红矩形左上角坐标 ( a1 , b1 ),右下角 ( a2 , b2 )。
根据重点公式,可以算出 O1=(x1+x22,y1+y22),O2=(a1+a22,b1+b22)O1 = ( \frac{ x1 + x2 }{2} , \frac{ y1 + y2 }{2} ) ,O2 = ( \frac{ a1 + a2 }{2} , \frac{ b1 + b2 }{2})O1=(2x1+x2,2y1+y2),O2=(2a1+a2,2b1+b2)。
所以相交的条件就是:
abs(x1+x22−a1+a22)<=x2−x12+a2−a12abs(\frac{ x1 + x2 }{2}-\frac{ a1 + a2 }{2})<=\frac{x2-x1}{2}+\frac{a2-a1}{2}abs(2x1+x2−2a1+a2)<=2x2−x1+2a2−a1
且
abs(y1+y22−b1+b22)<=y2−y12+b2−b12abs(\frac{ y1 + y2 }{2}-\frac{ b1 + b2 }{2})<=\frac{y2-y1}{2}+\frac{b2-b1}{2}abs(2y1+y2−2b1+b2)<=2y2−y1+2b2−b1
整理得
abs(x1+x2−a1−a2)<=x2−x1+a2−a1abs( x1 + x2 - a1 - a2)<=x2-x1+a2-a1abs(x1+x2−a1−a2)<=x2−x1+a2−a1
且
abs(y1+y2−b1−b2)<=y2−y1+b2−b1abs( y1 + y2 - b1 - b2)<=y2-y1+b2-b1abs(y1+y2−b1−b2)<=y2−y1+b2−b1
判断完相交,就是求相交部分的坐标了。
也很好看出来,左上角是 (max(x1,a1),min(x2,a2))( max(x1,a1) , min(x2,a2))(max(x1,a1),min(x2,a2)),右下角是(max(y1,b1),min(y2,b2))(max(y1,b1),min(y2,b2))(max(y1,b1),min(y2,b2))。
假的范围?
对于一些大得诡异的数据范围,可以先计算下是不是真的需要处理这么大的范围。
有时候数据大到一定程度可以直接输出不用考虑。
容斥原理
容斥原理中奇数个条件即相减,偶数个条件即相加。
树?
树的 子树、遍历 等问题考虑压成序列处理。




 本文深入解析了几何计算中的两个关键问题:点到链的距离计算公式及其几何意义,以及如何通过数学方法判断并计算两个矩形相交部分的坐标。通过详细推导,帮助读者理解算法背后的原理。
本文深入解析了几何计算中的两个关键问题:点到链的距离计算公式及其几何意义,以及如何通过数学方法判断并计算两个矩形相交部分的坐标。通过详细推导,帮助读者理解算法背后的原理。
















 3947
3947

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








