软件设计师-综合知识2

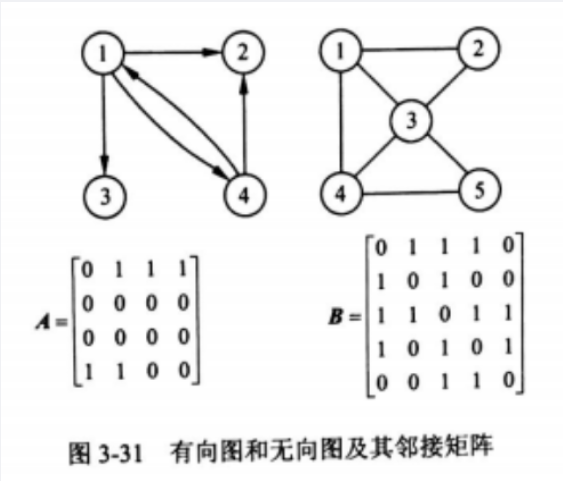
程序设计语言基础知识

基本概念

程序设计语言是为了书写计算机程序而人为设计的符号语言，用于对计算过程进行描述、组织和推导。

低级语言：机器语言(计算机硬件只能识别0和1的指令序列)，汇编语言

高级语言：功能更强，抽象级别更高，与人们使用的自然语言比较接近

各程序设计语言特点⭐

Fortran语言：科学计算，执行效率高。

Pascal语言：为教学开发，表达能力强

C语言：指针操作能力强，可以开发系统级软件，高效。

C++语言：面向对象，高效。

Java语言：面向对象，中间代码，跨平台

C#语言:面向对象，中间代码

.Net框架Python是一种面向对象、解释型计算机程序设计语言

Prolog是逻辑型程序设计语言。

汇编、解释和编译⭐

汇编：将汇编语言翻译成目标程序执行

解释和编译：将高级语言翻译成目标程序执行。不同之处在于编译程序生成独立的可执行文件，直接运行，运行时无法控制源程序，效率高。而解释程序不生成可执行文件，可以逐条解释执行，用于调试模式，可以控制源程序，因为还需要控制程序，因此执行速度慢，效率低。

语法、语义、语用⭐

程序设计语言定义三要素：语法、语义、语用

语法是指由程序设计语言的基本符号组成程序中的各个语法成分(包括程序)的一组规则，其中由基本字符构成的符号(单词)书写规则称为词法规则，由符号构成语法成分的规则称为语法规则。

语义是程序设计语言中按语法规则构成的各个语法成分的含义，可分为静态语义和动态语义。静态语义指编译时可以确定的语法成分的含义，而运行时刻才能确定的含义是动态语义。一个程序的执行效果说明了该程序的语义，它取决于构成程序的各个组成部分的语义。

语用表示了构成语言的各个记号和使用者的关系，涉及符号的来源、使用和影响

语言的实现则有个语境问题。语境是指理解和实现程序设计语言的环境，包括编译环境和运行环境。

程序设计语言的分类⭐

命令式和结构化程序设计语言，包括Fortran、PASCAL和C语言

面向对象程序设计语言，包括C++、JAVA和Smalltalk语言。

函数式程序设计语言，包括LISP、Haskell、Scala、Scheme、APL等。

逻辑型程序设计语言，包括PROLOG。

程序设计语言的基本成分⭐

数据成分：指一种程序设计语言的数据和数据类型。数据分为常量(程序运行时不可改变)、变量(程序运行时可以改变)全局量(存储空间在静态数据区分配)、局部量(存储空间在堆栈区分配)数据类型有整型、字符型、双精度、单精度浮点型、布尔型等。 运算成分：指明允许使用的运算符号及运算规则。包括算术运算、逻辑运算关系运算、位运算等。

控制成分：指明语言允许表述的控制结构。包括顺序结构、选择结构、循环结构。如下图所示。

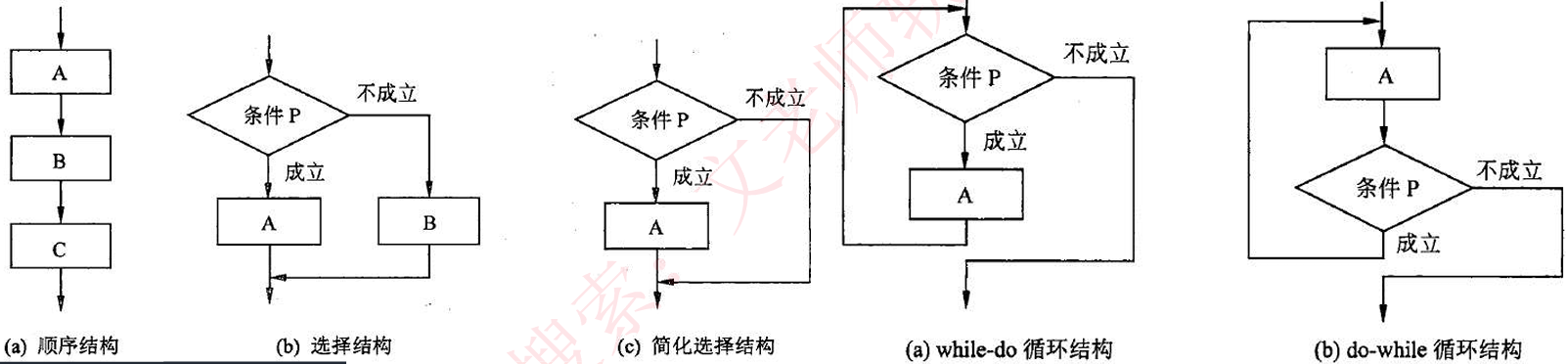
传输成分：指明语言允许的数据传输方式。如赋值处理、数据的输入输出等

函数

函数：C程序由一个或多个函数组成，每个函数都有一个名字，其中有且仅有一个名字为main的函数作为程序运行时的起点。函数的使用涉及3个概念:函数定义、函数声明和函数调用。

函数的定义包括两部分：函数首部和函数体。函数的定义描述了函数做什么和怎么做。函数定义的一般形式为:返回值的类型 函数名(形式参数表)//函数首部 函数体;

函数首部说明了函数返回值的数据类型、函数的名字和函数运行时所需的参数及类型。函数所实现的功能在函数体部分进行描述。

函数应该先声明后引用。如果程序中对一个函数的调用在该函数的定义之前进行，则应该在调用前对被调用函数进行声明。函数原型用于声明函数。函数声明的一般形式为 返回值类型 函数名(参数类型表);

函数调用的一般形式为:函数名(实参表);

函数调用时实参与形参间交换信息的方法有值调用和引用调用两种。

(1)值调用(Callby Value)。若实现函数调用时将实参的值传递给相应的形参，则称为是传值调用。在这种方式下形参不能向实参传递信息。在C语言中，要实现被调用函数对实参的修改，必须用指针作为参数。即调用时需要先对实参进行取地址运算，然后将实参的地址传递给指针形参。其本质上仍属于值调用。这种方式实现了间接内存访问。

(2)引用调用(Call by Reference)。引用是C++中引入的概念，当形式参数为引用类型时，形参名实际上是实参的别名，函数中对形参的访问和修改实际上就是针对相应实参所做的访问和改变。

将高级语言源程序翻译为可在计算机上执行的形式有多种不同的方式，其中()。

A.编译方式和解释方式都生成逻辑上与源程序等价的目标程序

B.编译方式和解释方式都不生成逻辑上与源程序等价的目标程序

C.编译方式生成逻辑上与源程序等价的目标程序,解释方式不生成

D.解释方式生成逻辑上与源程序等价的目标程序,编译方式不生成 答案:C

以下关于程序设计语言的叙述中，不正确的是()。

A.脚本语言中不使用变量和函数 B.标记语言常用于描述格式化和链接 C.脚本语言采用解释方式实现 D.编译型语言的执行效率更高 答案:A

函数f、g的定义如下，执行表达式“y=f(2)”的运算时，函数调用g(la)分别采用引用调用(call byreference)方式和值调用(call byvalue)方式，则该表达式求值结束后y的值分别为( )。

A.9、6 B.20、6 C.20、9 D.30、9 答案:B 引用调用：形参改变，值改变；值调用：形参改变，值不变

值调用

• f(2) 调用时，x = 2

• la = x + 1 = 3

• 调用 g(la)，此时 la = 3，由于是值调用，g 里的参数是 x=3 的副本：

  x = x * x + 1 = 3*3+1 = 10

  但这个 x 是局部变量，不影响原来的 la

• 所以，la 依然是 3，x 是原来 f 中的 x = 2

• 返回值是 la * x = 3 * 2 = 6

✅ 值调用结果：6

引用调用

• f(2) 调用时，x = 2

• la = x + 1 = 3

• 调用 g(la)，la 是以引用方式传递，即 g 里的 x 实际就是 f 里的 la 的别名：

  x = x * x + 1 = 3*3+1 = 10

  这时候，la 被修改成了 10

• 所以，la = 10，x = 2

• 返回值是 la * x = 10 * 2 = 20

✅ 引用调用结果：20

通用的高级程序设计语言一般都会提供描述数据、运算、控制和数据传输的语言成分，其中，控制包括顺序、( )和循环结构。

A.选择 B.递归 C.递推 D.函数 答案:A

编译程序基本原理

编译程序对高级语言源程序进行编译的过程中，要不断收集、记录和使用源程序中一些相关符号的类型和特征等信息，并将其存入符号表中，编译过程如下:

词法分析：是编译过程的第一个阶段。这个阶段的任务是从左到右一个字符一个字符地读入源程序，即对构成源程序的字符流进行扫描然后根据构词规则识别单词(也称单词符号或符号)。

语法分析：是编译过程的一个逻辑阶段。语法分析的任务是在词法分析的基础上将单词序列组合成各类语法短语，如“程序”，“语句”，“表达式”等等.语法分析程序判断源程序在结构上是否正确.

语义分析：是编译过程的一个逻辑阶段.语义分析的任务是对结构上正确的源程序进行上下文有关性质的审查,进行类型审查。如类型匹配、除法除数不为0等。又分为静态语义错误(在编译阶段能够查找出来)和动态语义错误(只能在运行时发现)

中间代码和目标代码：中间代码是根据语义分析产生的，需要经过优化链接最终生成可执行的目标代码。引入中间代码的目的是进行与机器无关的代码优化处理。常用的中间代码有后缀式(逆波兰式)、三元式(三地址码)、四元式和树等形式。需要考虑三个问题(一是如何生成较短的目标代码;二是如何充分利用计算机中的寄存器，减少目标代码访问存储单元的次数;三是如何充分利用计算机指令系统的特点，以提高目标代码的质量)

前缀表达式:+ab 中缀表达式:a+b 后缀表达式:ab+

主要掌握上述三种表达式即可，其实就是树的三种遍历，一般正常的表达式是中序遍历，即中缀表达式，根据其构造出树，再按题目要求求出前缀或后缀式

简单求法：后缀表达式是从左到右开始，先把表达式加上括号，再依次把运算符加到本层次的括号后面

将编译器的工作过程划分为词法分析，语法分析，中间代码生成时，语法分析阶段的输入是()若程序中的括号不配对，则会在()阶段检查出错误。 A、记号流 B、字符流 C、 源程序 D、分析树 A、词法分析 B、语法分析 C、语义分析 D、目标代码生成 答案:A B

以编译方式翻译C/C++源程序的过程中，()阶段的主要任务是对各条语句的结构进行合法性分析。 A.词法分析 B.语义分析C.语法分析 D.目标代码生成 答案:C

表达式(a-b)*(c+d)的后缀式(逆波兰式)是() A、abcd-+* B、ab-c+d* C、abc-d/_* D、ab-cd+* 答案:D 解析:使用快速解法，从左到右，先将表达式加上括号为((a-b)*(c+d))，再将符号移动到本表达式括号外面得((ab)-(cd)+)*，最后去掉括号得ab-cd+*

文法定义

字母表、字符串、字符串集合及运算

文法G是一个四元组，可表示为G=(VTPS)，其中:

V 非终结符，不是语言组成部分，不是最终结果，可以推导出其他元素。

T:终结符，是语言的组成部分，是最终结果，不能再推导其他元素。

S起始符，2S:是语言的开始符号。

P:产生式，用终结符代替非终结符的规则，例如a->b。

文法类型

乔姆斯基(Chomsky)把文法分成4种类型，即0型、1型、2型和3型

0型文法也称为短语文法，其功能相当于图灵机，任何0型语言都是递归可枚举的;反之，递归可枚举集也必定是一个0型语言。

1型文法也称为上下文有关文法，这种文法意味着对非终结符的替换必须考虑上下文，并且一般不允许替换成ε串。例如，若aAB→ayβ 是1型文法的产生式a和B不全为空，则非终结符A只有在左边是a，右边是β的上下文中才能替换成y

2型文法就是上下文无关文法，非终结的替换无须考虑上下文。程序设计语言中的大部分语法都是上下文无关文法，当然语义上是相关的，要注意区分语法和语义。 3型文法等价于正规式，因此也被称为正规文法或线性文法

语言中具有独立含义的最小语法单位是符号(单词)，如标识符、无符号常数与界限符等。词法分析的任务是把构成源程序的字符串转换成单词符号序列。

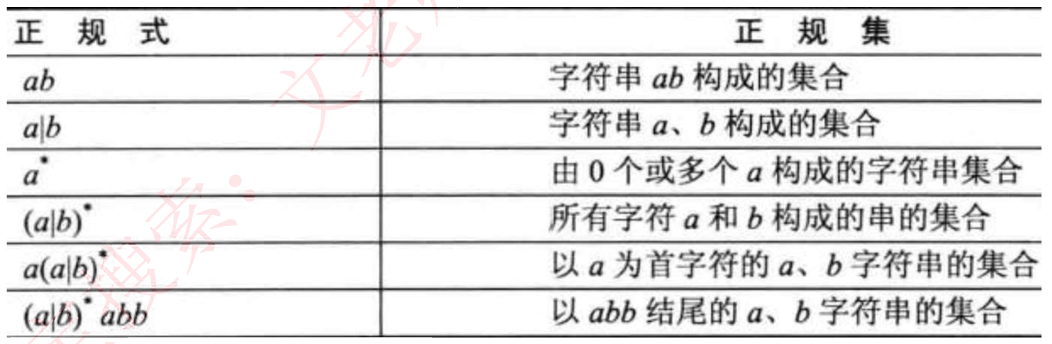
词法规则可用3型文法(正规文法)或正规表达式描述，它产生的集合是语言规定的基本字符集Σ(字母表)上的字符串的一个子集，称为正规集。正规式和正规集:

正规式

有限自动机

一个不确定的有限自动机也是一个五元不确定的有限自动机(NFA)2)组，它与确定有限自动机的区别如下。①f是SXz→2S上的映像。对于s中的一个给定状态及输入符号，返回一个状态的集合。即当前状态的后继状态不一定是唯一的。②)有向弧上的标记可以是ε。确定的有限自动机和不确定的有限自动机:输入一个字符，看是否能得出唯的后继，若能，则是确定的，否则若得出多个后继，则是不确定的。

下图所示为一个不确定有限自动机(NFA)的状态转换图，与该NFA等价的DFA是()

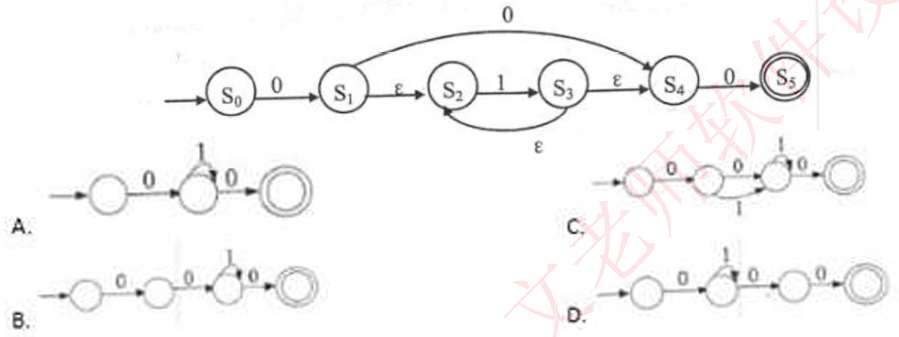
答案:C：看转换是否一致，0可以转换，1可以转换

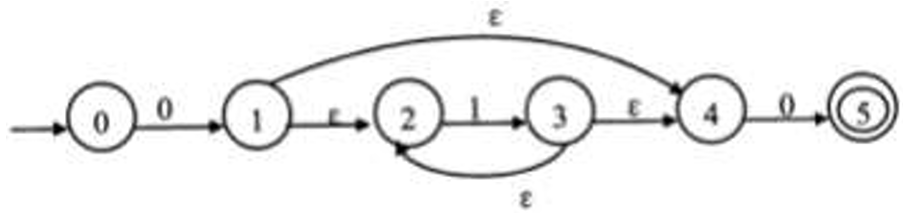
下图所示为一个不确定有限自动机(NFA)的状态转换图。该NFA可识别字符串()

A.0110 B.0101 C.1100 D.1010 答案:A

语法分析方法

自上而下语法分析:最左推导，从左至右。给定文法G和源程序串r。从G的开始符号S出发，通过反复使用产生式对句型中的非终结符进行替换(推导)，逐步推导出r。 递归下降思想:原理是利用函数之间的递归调用模拟语法树自上而下的构造过程，是一种自上而下的语法分析方法。 自下而上语法分析:最右推导，从右至左。从给定的输入串r开始，不断寻找子串与文法G中某个产生式P的候选式进行匹配，并用P的左部代替(归约)之，逐步归约到开始符号S。

移进-规约思想:设置一个栈，将输入符号逐个移进栈中，栈顶形成某产生式的右部时，就用左部去代替，称为归约。很明显，这个思想是通过右部来推导出左部，因此是自下而上语法分析的核心思想。

数据结构

数据结构+算法：综合知识10分，案例一道大题15分

线性表

1. 线性结构：每个元素最多只有一个出度和一个入度，表现为一条线状。线性表按存储方式分为顺序表和链表。

2. 存储结构：顺序存储:用一组地址连续的存储单元依次存储线性表中的数据元素，使得逻辑上相邻的元素物理上也相邻。

3. 链式存储：存储各数据元素的结点的地址并不要数据元素逻辑上相邻，物理上分开。

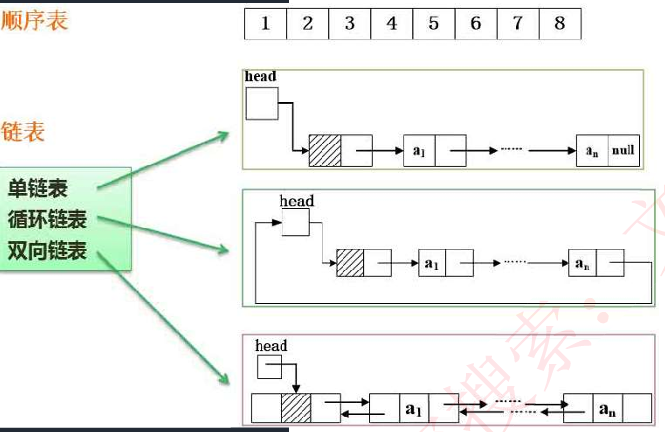
顺序存储和链式存储的对比如下图所示

因为链表还需要存储指针，因此有空间浪费存在在空间方面

在时间方面，当需要对元素进行破坏性操作(插入、删除)时，钱链表效率更高，因为其只需要修改指针指向即可，而顺序表因为地址是连续的，当删除或插入一个元素后，后面的其他节点位置都需要变动。

而当需要对元素进行不改变结构操作时(读取、查找)顺序表效率更高因为其物理地址是连续的，如同数组一般，只需按索引号就可快速定位，而链表需要从头节点开始，一个个的查找下去。

广义表是线性表的推广，是由0个或多个单元素或子表组成的有限序列。

广义表与线性表的区别:线性表的元素都是结构上不可分的单元素，而广义表的元素既可以单元素，也可以是有结构的表。

广义表一般记为:LS=(a1,a2,…，an)其中LS是表名，ai是表元素，它可以是表(称为子表)，也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数)n=0的广义表为空表;

而递归定义的重数就是广义表的深度，即定义中所含括号的重数(单边括号的个数，原子的深度为0，空表的深度为1

head()和tail():取表头(广义表第一个表元素，可以是子表也可以是单元素)和取表尾(广义表中，除了第一个表元素之外的其他所有表元素构成的表，非空广义表的表尾必定是一个表，即使表尾是单元素)操作

通过元素在存储空间中的相对位置来表示数据元素之间的逻辑关系，是()的特点。

A 顺序存储 B 链表存储 C 索引存储 D 哈希存储

正确答案:A 答案解析:线性表的存储结构分为顺序存储和链式存储。顺序存储是用一组连续的存储单元依次 存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。这种存 储方式下，元素间的逻辑关系无需占用额外的空间来存储。而链式存储是用通过指针链起来的节点来存储数据元素，这种存储结构下，进行插入 或删除，实质是对相关指针的修改。索引存储:分别存放数据元素和元素间关系的存储方式。哈希存储:哈希存储的基本思想是以关键字Key为白变量，通过一定的函数关系(散列函数或哈希函数)，计算出对应的函数值(哈希地址)，以这个值作为数据元素的地址，并将数据元素存入到相应地址的存储单元中。

在线性表L中进行二分查找，要求 L()。

A 顺序存储，元素随机排列 B 双向链表存储，元素随机排列 C 顺序存储，元素有序排列 D 双向链表存储，元素有序排列

正确答案:C 答案解析:线性表的二分查找也叫折半查找，它要求查找表必须是顺序存储并且按关键字有序排 列。因此，当需要对表进行插入或删除操作时，需要移动大量的元素，所以，折半查找适 用于表不宜变动且又经常进行查找的情况。

循环链表的主要优点是()。

A 不再需要头指针了 B 已知某个结点的位置后，能很容易找到它的直接前驱结点 C 在进行删除操作后，能保证链表不断开 D 从表中任一结点出发都能遍历整个链表

正确答案:D 答案解析:链表是用连续(或不连续)的存储单元存储数据元素，元素之间的逻辑关系用“指针”指明。链表具体分为几种形式:单向链表中结点包含一个指针，指明其直接前驱(或后继)元素结点:双向链表中结点包含两个指针，分别指明其直接前驱和直接后继元素结点:循环链表是最后结点的指针指回头结点，它可在任何位置上沿指针遍历整个链表。

已知一个线性表(38，25，74，63，52，48)，假定采用散列函数h(key)=key%7计算散列地址，并散列存储在散列表A[0..6中，若采用线性探测方法解决冲突，则在该散列表上进行等概率成功查找的平均查找长度为 A 1.5 B 1.7 C 2.0 D 2.3

正确答案: C 答案解析:按照散列函数h(key)=key%7和线性探测方法解决冲突将线性表(38，25，74，63，52，48)散列存储在散列表A[0..6)中如下图所示。

采用顺序表和单链表存储长度为n的线性序列，根据序号查找元素，其时间复杂度分别为()。

A 0(1)、0(1) B 0(1)、0(n) C o(n)、o(1) D 0(n)、0(n)

正确答案:B 答案解析:顺序表存储位置是相邻连续的，可以随即访问的一种数据结构，一个顺序表在使用前必须指定起长度，一日分配内存，则在使田中不可以动态的更改。他的优点是访问数据是比较方便，可以随即的访问表中的任何-个数据。链表是通过指针来描述元素关系的一种数据结构，他可以是物理地址不连续的物理空间。不能随访问链表元素，必须从表头开始，一步一步搜索元素。它的优点是:对于数组，可以动态的改变数据的长度，分配物理空间。因此两者的查找复杂度就显而易见了。

若线性表采用链式存储结构，则适用的查找方法为()。

A 随机查找 B 散列查找 C 二分查找 D 顺序查找

正确答案:D 答案解析:链式存储结构无法随机查找元素。以散列方式存储和查找元素时，元素的存储位置与其关键字相关，二分查找只能在有序顺序表中进行。

字符串“computer”中长度为3的子串有()个。

A 4 B5 C6 D 7

正确答案:C 答案解析:[由串中任意长度的连续字符构成的序列称为子串。对于字符串“computer”长度为 3的子串分别为“com”、“omp”、“mpu”、“put”、"ute”"ter"

若某线性表中最常用的操作是在最后一个元素之前插入和删除元素，则采用()最节省运算时间。

A 单链表 B 仅有头指针的单循环链表 C 仅有尾指针的单循环链表 D 双链表

正确答案: D 答案解析:链式存储有:单链表(线性链表)、循环链表、双向链表。单链表从链表的第一个表元开始，将线性表的节点依次存储在链表的各表元中。链表的每个表元除要存储线性表节点信息外，还要一个成分用来存储其后继节点的指针。循环链表是单链表的变形，其特点是表中最后一个节点的指针域指向头节点，整个链表形成一个环。因此，从表中的任意一个节点出发都可以找到表中的其他节点。循环链表中，从头指针开始遍历的结束条件不是节点的指针是否为空，而是是否等于头指针。为简化操作，循环链表中往往加入表头节点。双向链表的节点中有两个指针域，其一指向直接后继，另一指向直接前驱，克服了单链表的单向性的缺点。

在一个长度为n的带头结点的单链表h上，设有尾指针r，则执行()操作与链表的表长有关。

A 删除单链表中的第一个元素 B 删除单链表中的最后一个元素 C 在单链表第一个元素前插入一个新元素 D 在单链表最后一个元素后插入一个新元素

正确答案:B 答案解析: 删除单链表的最后一个结点需置其前驱结点的指针域为NULL,需要从头开始依次遍历找到该前驱结点，需要O(n),与表长有关。其他操作均与表长无关。

设有一个包含n个元素的有序线性表。在等概率情况下删除其中的一个元素，若采用顺序存储结构，则平均需要移动()个元素;若采用单链表存储，则平均需要移动()个元素。请回答第1个问题 A 1 B (n-1)/2 C logn D n

A 0 B 1 C (n-1)/2 D n/2

正确答案:B A 答案解析:本题考查数据结构基础知识。线性表是一个线性序列，在顺序存储方式下，若删除其中一个元素，需要将其后的元素逐个前移，使得元素之间没有空闲单元。表长为n时，共有n个可删除的元素，删除元素a1时需要移动n-1个元素，删除元素an时不需要移动元素，因此，等概率下删除一个元素时平均的移动元素次数Edelete为(n-1)/2。线性表若采用单链表存储，插入和删除元素的实质都是对相关指针的修改，而不需要移动元素。

线性表采用链表存储结构的特点中不包括()。

A 所需空间大小与表长成正比B 可随机访问表中的任一元素 C 插入和删除操作不需要移动元素 D 无须事先估计存储空间大小 正确答案:B 答案解析: A选项，链表每增加一个节点，数据存储空间随着变大,A选项正确B选项，链表元素由数据域和指针域组成，指针域用于指向直接后继的元素的地址，由于链表元素不一定是连续的，因此整个链表的存取必须从头指针开,B选项错误 C选项，插入和删除操作不需要移动元素，指向改变指针域的指向即可，C选项正确链表不需要连续的存储空间存储，因此无需实现估计存储空间大小，D选项正确D选项

关于链表操作中，说法正确的是( )

A 新增一个头结点需要遍历链表 B 新增一个尾结点需要遍历链表 C 删除最后一个节点需要遍历链表 D 删除第一个节点需要遍历链表

正确答案:C 答案解析:A选项:新增一个头结点通常只需要在链表的开始处插入一个新节点，并将它的?next?指针指向原链表的头结点(如果原链表非空的话)。这个过程并不需要遍历整个链表。B选项:新增一个尾结点通常意味着需要找到链表的最后一个节点，并将新节点的?next?指针设置为?null(或对应语言中的空值)，同时更新最后一个节点的?next?指针以指向新节点。但是，如果链表有一个指向尾部的指针(比如双向链表或某些特定设计的单链表)，那么就不需要遍历整个链表来找到尾结点.。C选项:为了删除链表的最后一个节点，我们需要找到倒数第二个节点(也就是原最后一个节点的前一个节点)，并将其?next?指针设置为?nul。由于我们没有直接指问最后一个节点的指针，所以通常需要遍历链表来找到它。D选项:删除链表的第一个节点(即头结点)通常只需要将头指针指向第二个节点(如果链表非空的话)这个过程并不需要遍历整个链表。因此，说法正确的是C。

栈和队列

基础知识

队列、栈结构如下图，队列是先进先出，分队头和队尾；栈是先进后出，只有栈顶能进出。循环队列设循环队列a 的容量为MAXSIZE，初始时队列为空，且Q.rear和Q.front 都等于0

1. 元素入队时修改队尾指针，即令Q.rear=(Q.rear+1)%MAXSIZE。

2. 元素出队时修改队头指针，即令Q.front=(Q.front+1)%MAXSIZE。

根据队列操作的定义，当出队操作导致队列变为空时，有Q.rear==Q.front;

若入队操作导致队列满，则a.rear==a.front。

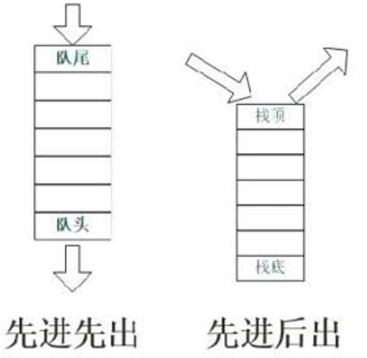
在队列空和队列满的情况下，循环队列的队头、队尾指针指向的位置是相同的，此时仅仅根据Q.rear和a.front之间的关系无法断定队列的状态。为了区别队空和队满的情况，可采用以下两种处理方式:其一是设置一个标志，以区别头、尾指针的值相同时队列是空还是满。其二是牺牲一个存储单元，约定以“队列的尾指针所指位置的下一个位置是队头指针时”表示队列满，如图所示，而头、尾指针的值相同时表示队列为空。

对于线性表，相对于顺序存储，采用链表存储的缺点是()

A.数据元素之间的关系需要占用存储空间，导致存储密度不高

B.表中结点必须占用地址连续的存储单元，存储密度不高

C.插入新元素时需要遍历整个链表，运算的时间效率不高

D.删除元素时需要遍历整个链表，运算的时间效率不高答案:A

若一个栈初始为空，其输入序列是1，2，3，…，n-1，n，其输出序列的第一个元素为k(1<k<[n/2」)，则输出序列的最后一个元素是()

A.值为n的元素 B.值为1的元素 C.值为n-k的元素 D.不确定的 答案:D

某双端队列如下图所示，要求元素进出队列必须在同一端口，即从A端进入的元素必须从A端出、从B端进入的元素必须从B 端出，则对于4个元素的序列e1、e2、e3、e4，若要求前2 个元素(e1e2)从A端口按次序全部进入队列，后两个元素(e3、e4)从B端口按次序全部进入队列，则可能得到的出队序列是()。

A.el、e2、e3、e4 B.e3、e4、el、el C.e2、e3、e4、e2 D.e4、e3、e2、el 答案:D

解析:根据题意，因为必须在同一端口进出队列，对于元素来说，相当于先进后出的栈，月A端口必须先e1后e2全部进入，那么e2出队列必然在e1之前，B端口必须先e3后e4全部进入，那么e4出队列必然在e3之前，只有D满足。

设循环队列的定义中有front和size两个域变量，其中Front表示队头元素的指针，SIZE表示队列的长度，如下图所示(队列长度为3，队头元素X，队尾元素为z)。设队列的存储空间容量为M，则队 尾元素的指针为()

栈实战

在程序的执行过程中，系统用()实现嵌套调用(递归调用)函数的正确返回

A 队列 B 优先队列 C 栈 D 散列表

正确答案:C 嵌套调用(递归调用)时，越晚被调用的函数越早返回结果，这与栈的“后进先出”属性相符。

设元素序列a、b、c、d、e、f经过初始为空的栈S后，得到出栈序列cedfba，则栈S的最小容量为()。

A 3 B4 C 5 D6

正确答案:B 答案解析: 根据题中出栈的顺序，当元素c出栈后，栈中有元素a、b，当元素e出栈之前，栈中有元素a、b、d、e，此时栈中的元素达到最多。因此栈s最小容量为4。

判断一个表达式中左右括号是否匹配，采用()实现较为方便。

A 线性表的顺序存储 B 队列 C 线性表的链式存储 D 栈

正确答案:D 答案解析:栈可以实现表达式中的括号匹配问题。当扫描到左括号时，则将其压入栈中:当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“”匹配，"”跟“”匹配，"”跟“”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式:否则，说明有未匹配的左括号，为非法格式。

下面关于栈和队列的叙述中，错误的是()。

A 栈和队列都是操作受限的线性表 B 队列采用单循环链表存储时，只需设置队尾指针就可使入队和出队操作的时间复杂度都为O(1) C 若队列的数据规模n可以确定，则采用顺序存储结构比链式存储结构效率更高 D 利用两个栈可以模拟一个队列的操作，反之亦可

正确答案:D 答案解析: 栈和队列都是操作受限的线性表:栈仅在表尾插入和删除元素;队列仅在表头删除元素、在表尾插入元素采用单循环链表表示队列的示意图如下图所示:

①入队时，新元素在an之后，若新元素节点指针为s，则在一般情况下入队操作序列表示为s->next=rear->next:rear->next=s:rear=s:。②出队时，将队头元素a，从队列中删除，一般情况下出队操作序列表示为:q=rear->next;//g指问队头元系所在节点 rear->next=q->next; free(q): 入队时初始队列为空、出队后队列变为空要进行特殊处理。入队操作和出队操作均与队列长度无关，因此其时间复杂度都为O(1)。队列是先入先出的线性表，栈是后进先出的线性表。一个线性序列经过队列结构后只能得到与原序列相同的元素序列，而经过一个栈结构后则可以得到多种元素序列。用两个栈可以模拟一个队列的入队和出队操作。

若栈采用顺序存储方式，现有两栈共享空间V[1..n],，top[]代表i( i=1,2)个栈的栈顶(两个栈都空时top[1]=1、top[2]= n),栈1的底在V[1],栈2的底在V[n],则栈满(即n个元素暂存在这两个栈)的条件是()。

A top[1]= top[2] B top[1]+ top[2]\==1 C top[1]+ top[2]\==n D top[1]- top[2]== 1

正确答案:D 最后一个栈元素的位置加1为栈满的情况，因此判断的条件就是top[1]-top[2]==1，选择D.

设有一个空栈，栈顶指针为1000H，每个元素需要一个存储单元，执行Push、Push、Pop、Push、Pop. Push、Pop、Push操作后，栈顶指针的值为()。 A 1002H B 1003H C 1004H D 1005H 正确答案:A 答案解析 : 每个元素需要一个存储单元，所以每入栈Push一次top加1，出栈Pop一次top减1.指针top的值依次是1001H,1002H,1001H,1002H,1001H,1002H,1001H1002H。

3个不同元素依次进展，能得到()种不同的出栈序列。A 4 B 5 C 6 D 7

正确答案:B 答案解析:)本次采用列举法，abc依次进栈的出栈序列有abc,acb,bac,bca,cba。

对于空栈S进行Push和Pop操作，入栈序列为a,b,c,d,e,进过Push、Push、Pop、Push、Pop、Push.Push、Pop操作后得到的出栈序列是()。

A b a,c B b a e C b,c,a D b,c,e

正确答案:D 答案解析: 出入栈操作的过程

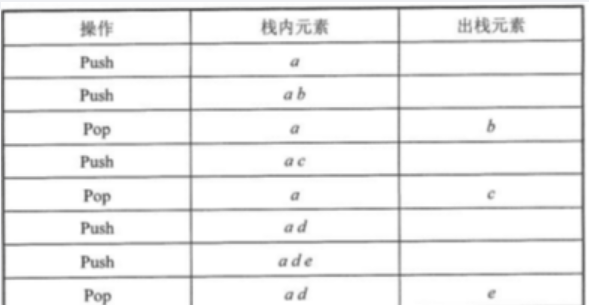
若元素以a,b,c,d,e的顺序进入一个初始为空的栈中，每个元素进栈、出栈各1次，要求出栈的第一个元素为d，则合法的出栈序列共有()种。A 4 B 5 C 6 D24

正确答案:A 答案解析:本题考查数据结构基础知识。栈的修改规则是后进先出。对于题目给出的元素序列，若要求d先出栈，则此时a、b、c尚在栈中，因此这四个元素构成的出栈序列只能是dcba。元素e可在c出栈之前进栈，之后c也只能在e出栈后再出栈，因此可以得到出栈系列decba。同理，e可在b出栈之前进栈，从而得到出栈序列dceba。若e在a出栈前入栈，则得到出栈序列dcbea。若e在a出栈后进、出栈，则得到出栈序列dcbae。

当执行函数时，其局部变量的存储一般采用()进行存储。

A 树形结构 B 静态链表 C 栈结构 D 队列结构 正确答案：C 答案解析:i调用函数时，系统会为调用者构造一个由参数表和返回地址组成的活动记录，并将记录压入系统提供的栈中，若被调用者有局部变量，也要压入栈中。

栈的特点是后进先出，若用单链表作为栈的存储结构，并用头指针作为栈顶指针，则()。

A 入栈和出栈操作都不需要遍历链表 B 入栈和出栈操作都需要遍历链表 C 入栈操作需要遍历链表而出栈操作不需要 D 入栈操作不需要遍历链表而出栈操作需要

正确答案:A 答案解析:本题考查数据结构基础知识。 单链表只能向后遍历，无法逆序遍历。

当函数调用执行时，在栈顶创建且用来支持被调用函数执行的一段存储空间称为活动记录或栈帧，栈帧中不包 括()

A 形参变量 B 全局变量 C 返回地址 D 局部变量

正确答案:B 当函数调用执行时，在栈顶创建并临时保留的一段存储空间即栈帧中，会存放调用函数时的返回地址、形参变量和局部变量。而全局变量存放在程序的静态存储区，位置是相对固定、独立的。

设栈初始时为空，对于入栈序列1,2,3…,n，这些元素经过栈之后得到出栈序列 P1，P2，P3,…，Pn.若p3=4，则p1，p2不可能的取值为(57)

A 6 5 B 2,3 C 3，1 D 3,5

正确答案:C 答案解析:本题中，A、B、D选项均可能发生。对于C选项，既然第一个入栈的元素1都已出栈，那么元素2必然在出栈序列中，所以P1,P2,P3不可能为3.1.4.

利用栈对算术表达式 10*(40-30/5)+20求值时，存放操作数的栈(初始为空)的容量至少为 ()，才能满足暂存该表达式中的运算数或运算结果的要求。A 2 B 3 C 4 D5 正确答案:C

在C/C++ 程序中，对于函数中定义的非静态局部变量，其存储空间在( )分配。

A 栈区 B 静态数据区 C 文本区 D 自由堆区

正确答案:A 答案解析: 非静态局部变量存储在栈区。

队列实战

设有栈S和队列Q且其初始状态为空，数据元素序列a,b,c,d,e,f依次通过栈S，且个元素从S出栈后立即进入队列Q，若出队列的序列是b,d,f,e,c,a，则S中的元素最多时，栈底到栈顶的元素依次为()。

A abc B acd C acef Dadfe

正确答案:C 答案解析: 队列Q的出队序列就是栈S的出栈序列，从b,d,fe,c,a反过来看ac,e,fd,b，如果后面元素的排列比前面的顺序靠后，就可以同时在栈里，由此只能是a,c,e,f。

采用循环队列的优点是()。

A 入队和出队可以在队列的同端点进行操作 B 入队和出队操作都不需要移动队列中的其他元素 C 避免出现队列满的情况 D 避免出现队列空的情况

正确答案:B 答案解析: 循环队列是将顺序队列形成一个环状结构，元素入队时修改尾指针，元素出队时修改头指针，入队和出队操作都不需要移动队列中的其他元素。

允许对队列进行的操作有()

A 对队列中的元素排序 B 去除最近进队列的元素

C 在队列元素之间插入元素 D 删除队头元素

正确答案:D 答案解析: 删除队头元素即出队。

为解决计算机主机与打印机之间速度不匹配问题，通常设置一个打印数据缓冲区，主机将要输出的数据依次写入该缓冲区，而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是()。

A 栈 B 队列 C 树 D 图

正确答案:B 答案解析: 提取数据的时候需要保持原来数据的顺序，因此对于缓冲区的要求是先进先出。

执行()操作时，需要使用队列作为辅助空间。

A 前序遍历二又树 B 深度优先搜索图 C 广度优先搜索图 D 查找哈希表

正确答案:C 答案解析: 广度优先搜索图类似于对二又树进行层次遍历，需要借助队列实现。

某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作。若元 素a、b、c、d依次全部入队列，之后进行出队列操作，则不能得到的出队序列是()。

A dbac B cabd C acdb D bacd

正确答案:C 答案解析:1假设仅左端可以出，左右两端都可以入，元素a、b、c、d依次全部入队列则可能出现以下几种入栈方式:第一种:a先从任意一端进入，然后b从左端进入，则为ba，然后c从右端进入，则为bac,接着d再从左端进入，则为dbac,最后再按照此顺序从左端出栈，因此A选项满足要求:第二种:a先从任意一端进入，然后b从右端进入，则为ab，然后c从左端进入，则为cab,接着d再从右端进入，则为cabd，最后再按照此顺序从左端出栈，因此B选项满足要求;第三种:a先从任意一端进入，然后b从左端进入，则为ba,然后c从右端进入，则为bac.接着d再从右端进入，则为bacd.最后再按照此顺序从左端出栈，因此D选项满足要求:C选项根据题干要求无法得出，因此选C。开发方法(结构化与面向对象)

某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作。若元素a、b、c、d依次全部入队列之后进行出队列操作，则不能得到的出队序列是()。

A dbac B cabd C acdb D bacd

正确答案: C 假设仅左端可以出，左右两端都可以入，元素a、b、c、d依次全部入队列则可能出现以下几种入栈方式:答案解析:第一种:a先从任意一端进入，然后b从左端进入，则为ba，然后c从右端进入，则为bac,接着d再从左端进入，则为dbac,最后再按照此顺序从左端出栈，因此A选项满足要求:第二种:a先从任意一端进入，然后b从右端进入，则为ab，然后c从左端进入，则为cab,接着d再从右端进入，则为cabd，最后再按照此顺序从左端出栈，因此B选项满足要求:第三种:a先从任意一端进入，然后b从左端进入，则为ba,然后c从右端进入，则为bac.接着d再从右端进入，则为bacd.最后再按照此顺序从左端出栈，因此D选项满足要求:C选项根据题干要求无法得出，因此选C。

字符串

字符串是一种特殊的线性表，其数据元素都为字符

空串:长度为0的字符串，没有任何字符。

空格串:由一个或多个空格组成的串，空格是空白字符，占一个字符长度。

子串:串中任意长度的连续字符构成的序列称为子串。含有子串的串称为主串，空串是任意串的子串。

串的模式匹配：子串的定位操作，用于查找子串在主串中第一次出现的位置的算法。

模式匹配算法

朴素的模式匹配算法：也称为布鲁特一福斯算法，其基本思想是从主串的第1个字符起与模式串的第1个字符比较，若相等，则继续逐个字符进行后续的比较否则从主串中的第2个字符起与模式串的第1个字符重新比较，直至模式串中每个字符依次和主串中的一个连续的字符序列相等时为止，此时称为匹配成功，否则称为匹配失败。

KMP算法⭐

对基本模式匹配算法的改进，其改进之处在于：每当匹配过程中出现相比较的字符不相等时，不需要回溯主串的字符位置指针，而是利用已经得到的“部分匹配”结果将模式串向右“滑动”尽可能远的距离，再继续进行比较。当模式串中的字符pj与主串中相应的字符si 不相等时，因其前i 个字符("p0...pj-1")已经获得了成功的匹配，所以若模式串中"p0..pk-1"与"pj-k...pj-1'相同，这时可令pk与si进行比较，从而使i无须回退。在KMP算法中，依据模式串的next函数值实现子串的滑动。若令next[j]=k，则next[i]表示当模式串中的pj与主串中相应字符不相等时，令模式串的next[i]与主串的相应字符进行比较

在字符串的KMP模式匹配算法中，需先求解模式串的next函数值，其定义如下式所示，j表示模式串中字符的序号(从1开始)。若式串p为“abaac”，则其next函数值为()。

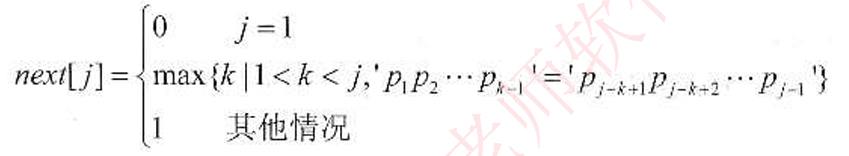
A.01234 B.01122 C 01211 D.01111

答案:B：KMP是进行字符串模式匹配运算效率较高的算法。根据对next函数的定义，模式串前两个字符的next值为0、1。对于第3个字符“a”，其在模式串中的前缀为“ab”从该子串找不出前缀和后缀相同的部分，因此，根据定义，该位置字符的next值为1。对于第4个字符“a”，其在模式串中的前缀为“aba”，该子串只有长度为l的前缀“a”和后缀“a”相同，根据定义，该位置字符的next值为2。对于第5个字符“a”，其在模式串中的前缀为“abaa”，该子串只有长度为1的前缀“a”和后缀“a”相同，根据定义，该位置字符的next值为2。综上可得，模式串“abaac”的next函数值为01122。

数组

数组是定长线性表在维度上的扩展，即线性表中的元素又是一个线性表。N维数组是一种“同构”的数据结构，其每个数据元素类型相同、结构一致。

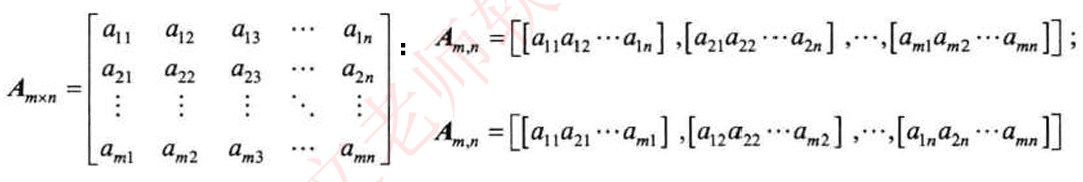
其可以表示为行向量形式或者列向量形式线性表，单个关系最多只有一个前驱和一个后继，本质还是线性的。数组结构的特点:数据元素数目固定:数据元素类型相同;数据元素的下标关系具有上下界的约束且下标有序。数组数据元素固定，一般不做插入和删除运算，适合于采用顺序结构

数组存储地址的计算，特别是二维数组，要注意理解，假设每个数组元素占用存储长度为len，起始地址为a，存储地址计算如下(默认从0开始编号)：

特殊矩阵：矩阵中的元素(或非0元素)的分布有一定的规律。常见的特殊矩阵有对称矩阵、三角矩阵和对角矩阵。

稀疏矩阵：在一个矩阵中，若非零元素的个数远远少于零元素个数，且非零元素的分布没有规律。 存储方式为三元组结构，即存储每个非零元素的(行列，值)。

代入特殊值即可

最大子段和问题描述为，在n个整数(包含负数)的数组A中，求元素之和最大的非空连续子数组，如数组A=(-2，11，-4，13，-5，-2)，其子数组B=(11，-4，13)具有最大子段和 20(11-4+13=20)。求解该问题时，可以将数组分为两个n/2个整数的子数组最大子段和或者在前半段，或者在后半段，或者跨越中间元素，通过该方法继续划分问题，直至最后求出最大子段和，该算法的时间复杂度为()。

A O(nlgn) B O(n^2) C 0(n^2lgn) D O(n^3)

正确答案:A 答案解析:根据题干描述“求解该问题时，可以将数组分为两个n/2个整数的子数组最大子段和或者在前半段，或者在后半段，或者跨越中间元素，通过该方法继续划分问题，直至最后求出最大子段和”。可知采用的是分治法求解，时间复杂度为O(nlgn)。

在一个二维数组A中，假设每个数组元素的长度为3个存储单元，行下标i为0-8，列下标i为0-9，从首地址SA开始连续存放，在这种情况下，元素A[8][5]的起始地址为()。 A SA+141 B SA+144 C SA+222 D SA+255 正确答案:D 答案解析:二维数组计算地址(按照行优先顺序)的公式为:LOC(ij)=LOC(0,0)+(i*m+j)*L其中LOC(0,0)=SA，是数组存放的首地址，L=3是每个数组元素的长度:m=9-0+1=10是数组的列数内此LOC(85)=SA+(8*10+5)*3=SA+255，选D

已知二维数组A按行优先方式存储，每个元素占用两个存储单元，第一个元素A[0][0]的地址为100，元素A[3][3]的存储地址是220，则元素A[5][5]的地址是()。 A 300 B 310 C 306 D 296 正确答案:A 答案解析:数组列是固定的，根据A[0，0]是100，A[3，3]是220，算一下一行有多少列。后者位于第四行第四列，根据220-4=216，就能得到前三行是从100到216，一共是117个数，117除以3得到39，也就是一行有39列。A[5，5]位于第六行第六列，所以就是5*39+6=201，所以从[0，0到[5，5]一共是201个数,又因为是从100开始算，所以A[5，5]存储的是300.

矩阵

()是对稀疏矩阵进行压缩存储的方式

A 二维数组和双向链表 B 三元组顺序链表和十字链表, C 邻接矩阵和十字链表 D 索引顺序表和双向链表

正确答案:B 答案解析:对稀疏矩阵的压缩方法有三种:三元组顺序表、行逻辑连接的顺序表、十字链表

有一个n*n的对称矩阵A，将其下三角部分按行存放在一个一维数组B中，而A[0][0]存放在B[0]中，则第i+1行的对角元素而A存放在B中的()处。

A (i+3)*i/2 B (i+1)*i/2 C (2n-i+1)*i/2 D (2n-i-1)*i/2

正确答案:A 答案解析:矩阵下标自0开始，数组下标自0开始，矩阵按行优先存放在数组中。可以使用代入法，A[1][1]=B[2]代入选择A

设图的邻接矩阵A如下所示，各顶点的出度分别为()。

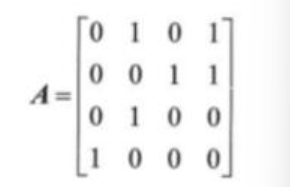
正确答案:C 邻接矩阵A为非对称矩阵，说明图是有向图，各顶点的出度为矩阵行中1的个数，即2,2,1,1。

将三对角矩阵A[1..100][1..100]按行优先存入一维数组B[1..298]中，A中元素A[66][65]在数组B中的位置k为 A 198 B 195 C 197 D 196 正确答案:B 答案解析: 对于三对角矩阵，将A[1.n][1.n]压缩至B[1..3n-2]时，ai与bk的对应关系为k=2i+j-2。则A中的元素A[66][65]在数组B中的位置k=2*66+65-2=195

下列哪种图的邻接矩阵是对称矩阵()。

A 有向图 B 无向图 C AOV网 D AOE网

正确答案:B 答案解析: 无向图的邻接矩阵存储中，每条边存储两次，且A=A[j][i]。

在含有n个顶点和e条边的无向图的邻接矩阵中，零元素的个数是()。

A e B 2e C n^2-e D n^2-2e

正确答案:D 无向图的邻接矩阵中，邻接大小为n\^2，非零元素个数为2e，所以零元素的个数是n^2-2e。

对有n个结点、e条边且采用数组表示法(即邻接矩阵存储)的无向图进行深度优先遍历,时间复杂度为()。 A O(n^2) B 0(e2) C O(n+e) D O(n*e) 正确答案:A 答案解析:图的邻接矩阵是指用一个矩阵来表示图中顶点之间的关系。对有n 个结点的图，其邻接矩阵是一个n阶方阵。对于无向图来说，其邻接矩阵如下图所示

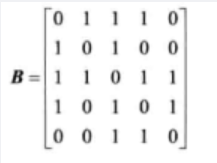
当采用深度优先进行遍历的时候，查找所有邻接点所需要的时间是O(n^2)。

若无向图G有n个顶点e条边，则G采用邻接矩阵存储时，矩阵的大小为()

A n*e B n^2 C n2+e2 D (n+e)2

正确答案:B 答案解析: 对于具有n个顶点的图 G=(V，E)，其邻接矩阵是一个n阶方阵，且是对称的。因此矩阵的大小为n^2

设一个包含N个顶点、E条边的简单无向图采用邻接矩阵存储结构(矩阵元素A等于I/0分别表示顶点i与顶点j之间有/无边)，则该矩阵中的非零元素数目为()。 A N B E C 2E D N+E

正确答案:C 答案解析:本题考查数据结构的基础知识。无向图的邻接矩阵是一个对称矩阵，每条边会表示两次，因此矩阵中的非零元素数目为2E。

设一个包含N个顶点、E条边的简单有向图采用邻接矩阵存储结构(矩阵元素Ai等于1/0分别表示顶点i与顶点i之间有/无弧)，则该矩阵的元素数目为()，其中非零元素数目为()。请回答第1个问题 A E^2 B N^2 C N\^2-E^2 D N\^2+E^2 正确答案:B 答案解析: 本题考查数据结构中图的存储结构。 对于一个具有n个顶点的图，其邻接矩阵为n*n个元素的矩阵。无向图的邻接矩阵是对称矩阵，如下图(a)所示。对于有向图，其邻接矩阵中非零元素的数目表示有向弧的个数。有向图的邻接矩阵如下图(b)所示。

对下列有向图的邻接矩阵，进行深度遍历的次序是()

v1-v2-v3-v4-v5-v6 v1-v4-v2-v3-v5-v6 v1-v2-v3-v5-v4-v6 v1-v2-v5-v4-v3-v6

图的深度优先遍历(DFS)遍历:①首先，选取图中某一顶点vi作为起始点访问;②任意选取一个与vi邻接的顶点，且该顶点未被访问，一直重复下去，直到图中所有与vi连通的顶点都被访问到;【可概括为由起始顶点开始，沿着一条路径尽可能地深入搜索该图，直到无法再继续下去】③若还有顶点未被访问到，则另外选取一个未被访问的顶点再次作为起始点，回溯到上一个未访问的顶点重复以上步骤，直至图中所有结点都被访问。A选项属于层次遍历，不满足题目要求B选项遍历V1之后应该遍历V2或V3，因此错误D选项谝历V4之后，应先遍历V6,因此错误答案因此选C。

树

基本概念

当n=0时称为空树，在任一颗非空树中，有且仅有一树是n个节点的有限集合(n>=0)个根节点。其余结点可分为m(m20)个互不相交的有限子集T1，T2，…，Tm，其中，每个Ti又都是一棵树，并且称为根结点的子树。树的基本概念如下:

1. 双亲、孩子和兄弟。结点的子树的根称为该结点的孩子;相应地，该结点称为其子结点的双亲。具有相同双亲的结点互为兄弟。

2. 结点的度。结点的子树个数记为该结点的度。例如A的度为3，B的度为2，C的度为0，D的度为1。

3. 叶子结点。叶子结点也称为终端结点，指度为0的结点。例如，E、F、C、G都是叶子结点。

4. 内部结点。度不为0的结点，也称为分支结点或非终端结点。除根结点以外，分支结点也称为内部结点。例如，B、D都是内部结点。

5. 结点的层次。根为第一层，根的孩子为第二层，依此类推，若某结点在第i层，则其孩子结点在第i+1层。例如，A在第1层，B、C、D在第2层，E、F和G在第3层。

6. 树的高度。一棵树的最大层数记为树的高度(或深度)。例如，图中所示树的高度为3.

7. 有序(无序)树。若将树中结点的各子树看成是从左到右具有次序的，即不能交换则称该树为有序树，否则称为无序树。

二叉树

二叉树（binary tree）是非线性数据结构，代表“祖先”与“后代”之间的派生关系，体现了“一分为二”的分治逻辑。与链表类似，二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用。

每个节点都有两个引用（指针），分别指向左子节点和右子节点，该节点被称为这两个子节点的父节点（parent node）。当给定一个二叉树的节点时，我们将该节点的左子节点及其以下节点形成的树称为该节点的左子树（left subtree），同理可得右子树（right subtree）。

在二叉树中，除叶节点外，其他所有节点都包含子节点和非空子树。如图所示，如果将“节点 2”视为父节点，则其左子节点和右子节点分别是“节点 4”和“节点 5”，左子树是“节点 4 及其以下节点形成的树”，右子树是“节点 5 及其以下节点形成的树”。

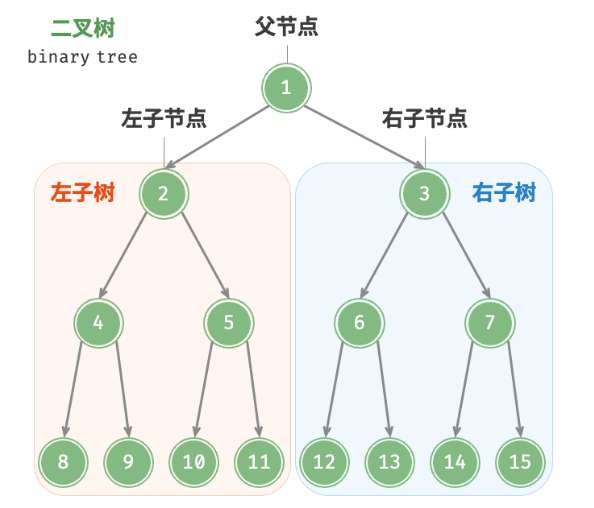
二叉树是n个节点的有限集合，它或者是空树，或者是由一个根节点及两颗互不相交的且分别称为左、右子树的二叉树所组成

两种特殊的二叉树如下图所示:

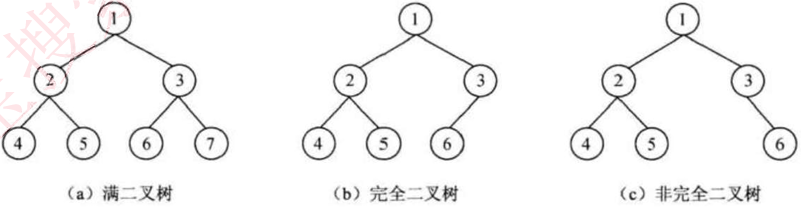
二叉树常见术语

二叉树有一些性质如下，要求掌握，在实际考试中可以用特殊值法验证。

1. 二叉树第i层(i>1)上至多有2^(i-1)个节点。

2. 深度为k的二叉树至多有2^k一1个节点(k>1)

3. 对任何一棵二叉树，若其终端节点数为n0，度为2的节点数为n2，则n0=n2+1.

此公式可以画一个简单的二叉树使用特殊值法快速验证，也可以证明如下:设一棵二叉树上叶结点数为n，单分支结点数为n，双分支结点数为n，则总结点数=n。+n,+n,。在一棵二叉树中，所有结点的分支数(即度数)应等于单分支结点数加上双分支结点数的2倍，即总的分支数=n,+2n,。由于二叉树中除根结点以外每个结点都有唯一的一个分支指向它，因此二叉树中:总的分支数=总结点数-1。 (4)具有n个节点的完全二叉树的深度为|log2 n」+1。

二叉树的常用术语如图 7-2 所示。

• 根节点（root node）：位于二叉树顶层的节点，没有父节点。

• 叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。

• 边（edge）：连接两个节点的线段，即节点引用（指针）。

• 节点所在的层（level）：从顶至底递增，根节点所在层为 1 。

• 节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。

• 二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。

• 节点的深度（depth）：从根节点到该节点所经过的边的数量。

• 节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

实战演练

在一颗非空二叉树中，叶子节点的总数比度为2的节点总数多()个。 A -1 B 0 C 1 D 2

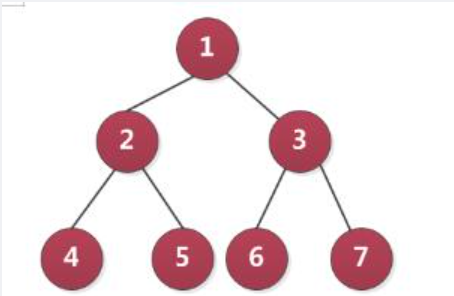
正确答案:C 任意画一个非空二叉树，如图。可以看出叶子结点有4个，度为2的结点有3个。

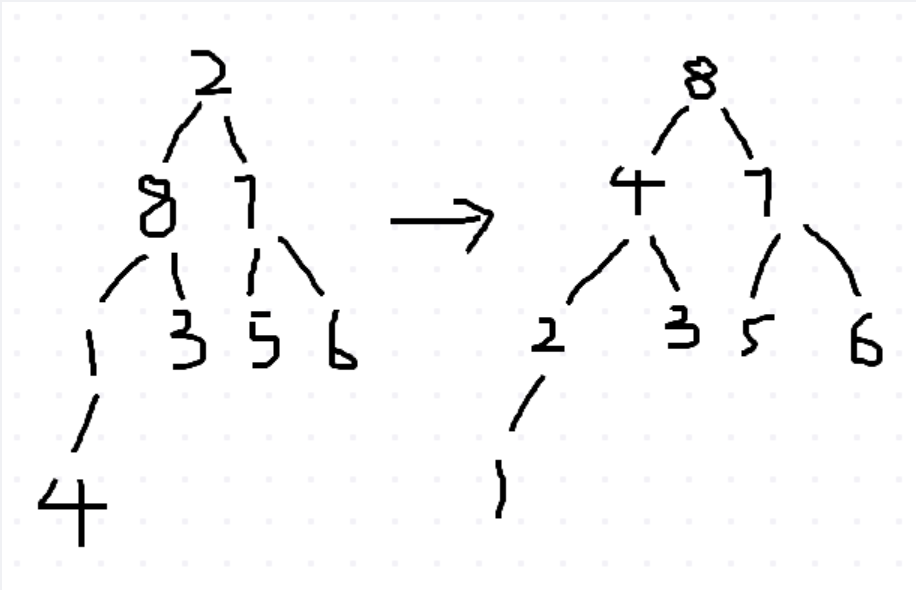
对数组A=(2,8,7,1,3,5,6,4)构建大顶堆为()(用数组表示)

A (1,2,3,4.5,6,7.8) B (1,2,5,4, 3,7,6 8) C (8.472 3 5 6 1). D (8,7,6,5,4.3,21) 正确答案:C 答案解析:1、先按照元素顺序构造二叉树2、选择第一个最大的非叶子节点，与其两个孩子(若有)分别进行比较，如果比孩子小，则与孩子交换位置3、重复1、2过程知道父节点比孩子结点都大为止。如下图所示:

一棵度为4的数T中，若有5个度为4的结点，7个度为3的结点，3个度为2的结点，9个度为1的结点，则树T的叶子结点个数()。 A 30 B 31 C 32 D 33 正确答案:D 答案解析: 根据树中结点总数为n,n=分支数+1，而分支数等于树中各个节点的度之和，所以根据此:5*4+7*3+3*2+9*1+1=叶子数+5+7+3+9;因此叶子数为33个。

分别以以下序列构造二叉排序树，与其他3个序列所构造的结果不同的是()。 A 100,80,90,60,120,110,130 B 100,120,110,130,80,60,90

C 100,60,80,90,120,110,130 D 100,80,60,90,120,130,110

正确答案:C 答案解析: ABD中100的左孩子根结点是80，C中100左孩子的根结点是60.

关于二叉树的说法正确的是()。

A 深度为k的二叉树最多有2k-1个结点(k≥1) B 深度为k的二叉树最多有2\^k-1个结点(k≥1)

C 深度为k的二又树最多有2^(k-1)个结点(k≥1) D 深度为k的二又树最多有2^k个结点(k≥1)

正确答案:B 答案解析: 深度为k的二又树最多有2^k-1个结点(k>=1)

下面关于二叉树的叙述，正确的是 ()。

A 完全二又树的高度h与其节点数n之间存在确定的关系 B 在二叉树的顺序存储和链式存储结构中，完全二又树更适合采用链式存储结构 C 完全二又树中一定不存在度为1的节点 D 完全二叉树中必定有偶数个叶子节点 正确答案:A 根据其定义，一棵完全二叉树除了最后一层外，其余层的节点数都是满的，最后一层的节点也必须自左至右排列，例如图(a)是高度为3的满二叉树，图(b)是完全二叉树，图(c)不是完全二叉树。

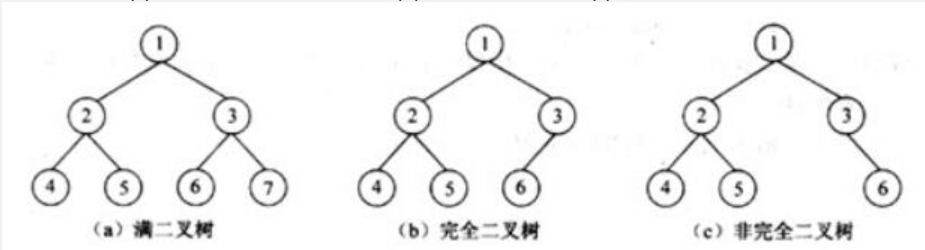
二叉树采用顺序存储结构时，对于编号为i的节点，则有: 若i=l时，该节点为根节点，无双亲: 若i>|时，该节点的双亲节点为|i/2|: 若2i≤n，则该节点的左孩子编号为2i否则无左孩子:·若2i+1≤n，则该节点的右孩子编号为2i+1，否则无右孩子。图(d)为具有10个节点的完全二叉树及其顺序存储结构，图(e)为某非完全二叉树的顺序存储结构，从中可以看出，完全二又树适合采用顺序存储结构。

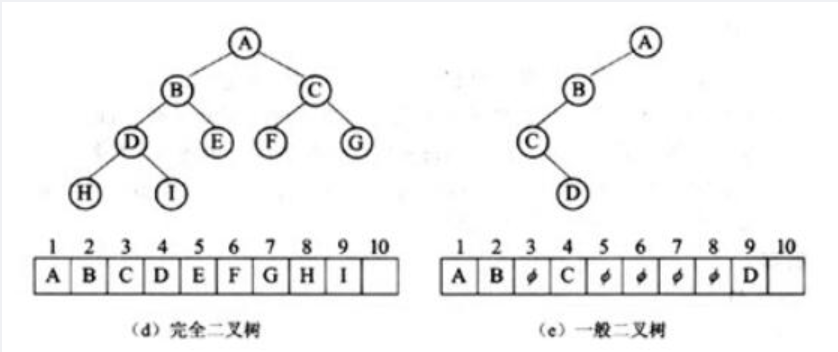
可以推导出具有n个节点的完全二又树的深度为[log2n]+1。

二叉树的高度是指其层数，空二叉树的高度为0，仅有根结点的二叉树高度为1。若某二叉树中共有1024个结点，则该二叉树的高度是整数区间()中的任一值。 A (10, 1024) B [10, 1024] C (11, 1024) D [11, 1024] 正确答案:D 本题分三种情况，第一种1024个结点排列成单枝树，即非叶子结点只有一个孩子的树。该二又树的高度为答案解析:1024。第二种情况是完全二叉树的情况，根据二叉树特性:具有n个结点的完全二叉树的深度为llog2nl+1，可得二叉树深度为11.第三种情况是非完全二叉树，层数在12-1023之间。综上所述，该二叉树的层数是整数区间[11,1024]中的任一值。

已知树T的度为4，且度为4的结点数为7个、度为3的结点数5个、度为2的结点数为8个、度为1的结点数为10个，那么T的叶子结点个数为()。(注:树中节点个数称为结点的度，结点的度中的最大值称为树的度。) A 30 B 35 C 40 D49 正确答案:C

一棵有n个结点的树的所有结点的度数之和为()。

A n-1 B n C n+1 D 2n

正确答案:A 答案解析: 这道题有点偏，可以当成一个常识。除了根结点之外，其他每个结点都是某个结点的孩子结点，因此树中所有结点的度数加1等于结点数。

设m和n是某二叉树上的两个结点，中序遍历时，n排在m之前的条件是58。

A m是n的祖先结点 B m是n的子孙结点 C m在n的左边 D m在n的右边

正确答案:D对于二叉树的中序遍历，是先遍历根结点的左子数，再访问根结点，最后遍历根结点的右子树。所以结点n在m的左边，也就是m在n的右边。

以下关于m阶B-树的说法中，错误的是

A 根结点最多有m棵子树 B 所有叶子结点都在同一层次上 C 结点中的关键字有序排列 D 叶子结点通过指针链接为有序表

正确答案:D 答案解析:一棵m阶的B树中每个结点最多有m棵子树，所有的叶子结点都出现在同一层次上，有k颗子树的非叶子结点有k-1个键，键按照递增顺序排列。叶子叶子结点之间不相连。作为对比，B+树有k颗子树的非叶节点有k个键，键按照递增顺序排列。所有的叶子结点中包含了完整的索引信息，包括指向含有这些关键字记录的指针，中间节点每个元素不保存数据，只用来索引。叶子结点本身依关键码的大小自小而大的顺序链接

对n个元素的有序表A[i,j]进行顺序查找，其成功查找的平均查找长度(即在查找表中找到指定关键码的元素时，所进行比较的表中元素个数的期望值)为()。

A n B (n+1)/2 C log2n D n2

正确答案:B 答案解析: 本题考查顺序查找方法。假设从前往后找，则所找元素为第1个元素时，与表中的1个元素作了比较，所找元素为第2个元素时，与表中的2个元素作了比较，…，所找元素为第n个元素时，与表中的n个元素作了比较，因此，平均查找长度等于(1+2+...+n)/n。

一个高度为k的满二叉树的结点总数为2h-1，从根结点开始，向上而下、同层次结点从左至右，对结点按照顺席依次编号，即根结点编号为1，其左、右孩子结点编号分为2和3，再下一层从左到右的编号为4、5、6.7，依次类推。那么，在一颗满二叉树中，对于编号为m和n的两个结点，若n=2m+1，则( 56)结点。

A m是n的左孩子 B m是n的右孩子 C n是m的左孩子 D n是m的右孩子

正确答案:D 由于改二叉树为满二叉树，且根节点编号从1开始，由满二叉树的性质可知父结点m和右孩子n之间的关系为n=2m+1，本颖选择D选项。如果是购买标准产品，且数量不大，则使用单边合同。

设由三棵树构成的森林中，第一棵树、第二棵树和第三棵树的结点总数分别为 n1、n2 和n3。将该森林转换为一棵二叉树，那么该二又树的右子树包含()个结点

A n1 B n1+n2 C n3 D n2+n3 正确答案:D

对于一棵树，每个结点的孩子个数称为结点的度，结点度数的最大值成为树的度。某树T的度为4，其中有5个度为4的结点，8个度为3的结点，6个度为2的结点，10个度为1的结点，则T中的叶子结点个数为()。 A 38 B 29 C 66 D 57

正确答案:A答案解析:设度为0的叶子结点数为n0,度为1的结点数为n1，度为2的结点数为n2，度为3的结点数是n3，度为4的结点数为n4，根据边和结点的关系我们可以得到等式n0+n1+n2+n3+n4=10*n1+6*n2+8*n3+5*n4+1,其中+1表示加上根结点，求解可得n0=38。

森林的叶子节点是()

A 二又树中没有左孩子的节点 B 二叉树中没有右孩子的节点 C 森林中度为0的节点 D 二叉树中度为1的节点

正确答案:C 答案解析: 叶子节点指的是度为0的节点。

当一棵非空二叉树的()时，对该二叉树进行中序遍历和后序遍历所得 的序列相同。

A 每个非叶子结点都只有左子树 B 每个非叶子结点都只有右子树 C 每个非叶子结点的度都为1 D 每个非叶子结点的度都为2

正确答案:A 中序遍历的顺序是左根右，后序遍历的顺序是左右根，若每个非叶子节点都只有左子树，那中序后序的遍历顺序此时可以简单的看成是左根，二者所得的序列一致，因此答案选择A选项。

顺序存储结构

顺序存储，就是用一组连续的存储单元存储二叉树中的节点，按照从上到下从左到右的顺序依次存储每个节点。

对于深度为k的完全二叉树，除第k层外，其余每层中节点数都是上一层的两倍，由此，从一个节点的编号可推知其双亲、左孩子、右孩子结点的编号。假设有编号为i的节点，则有:若i=1，则该节点为根节点，无双亲;若i>1，则该节点的双亲节点为Iv2l若2isn，则该节点的左孩子编号为2i，否则无左孩子。若2i+1sn，则该节点的右孩子编号为2i+1，否则无右孩子 显然，顺序存储结构对完全二叉树而言既简单又节省空间，而对于一般二叉树则不适用。因为在顺序存储结构中，以节点在存储单元中的位置来表示节点之间的关系，那么对于一般的二叉树来说，也必须按照完全二叉树的形式存储也就是要添上一些实际并不存在的“虚节点”，这将造成空间的浪费

二叉树的链式存储结构由于二叉树中节点包含有数据元素、左子树根、右子树根及双亲等信息，因此可以用三叉链表或二叉链表(即一个节点含有三个指针或两个指针)来存储二叉树，链表的头指针指向二叉树的根节点

常见二叉树类型

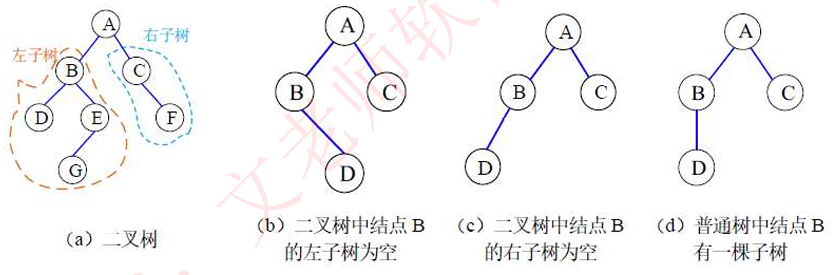
1. 完美二叉树

如图 7-4 所示，完美二叉树（perfect binary tree）所有层的节点都被完全填满。在完美二叉树中，叶节点的度为 0 ，其余所有节点的度都为 2 ；若树的高度为 h ，则节点总数为 2h+1−1 ，呈现标准的指数级关系，反映了自然界中常见的细胞分裂现象。

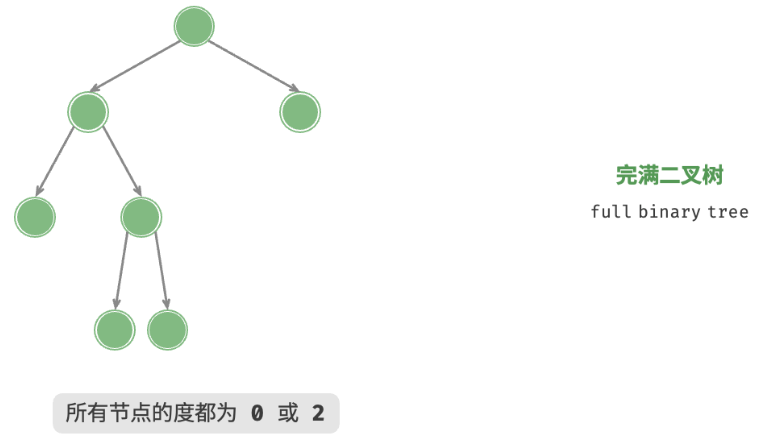
3. 完满二叉树

完满二叉树（full binary tree）除了叶节点之外，其余所有节点都有两个子节点。

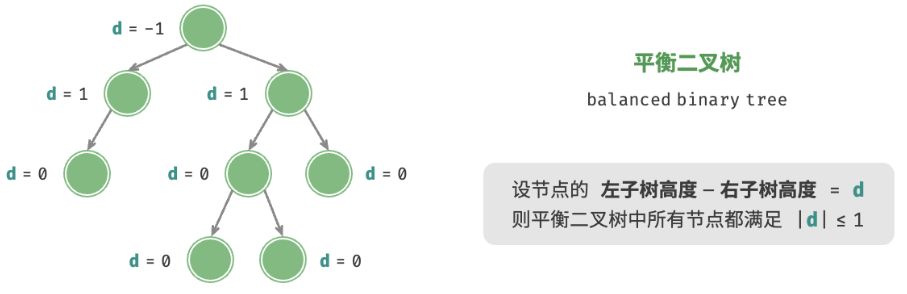
4. 平衡二叉树

平衡二叉树（balanced binary tree）中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。

二叉树遍历

基本概念

从物理结构的角度来看，树是一种基于链表的数据结构，因此其遍历方式是通过指针逐个访问节点。然而，树是一种非线性数据结构，这使得遍历树比遍历链表更加复杂，需要借助搜索算法来实现。

二叉树常见的遍历方式包括层序遍历、前序遍历、中序遍历和后序遍历等。一颗非空的二叉树由根节点、左子树、右子树三部分组成，遍历这三部分也就遍历了整颗二叉树。这三部分遍历的基本顺序是先左子树后右子树，但根节点顺序可变，以根节点访问的顺序为准有下列三种遍历方式:

1. 先序(前序)遍历:根左右

2. 中序遍历:左根右

3. 后序遍历:左右根

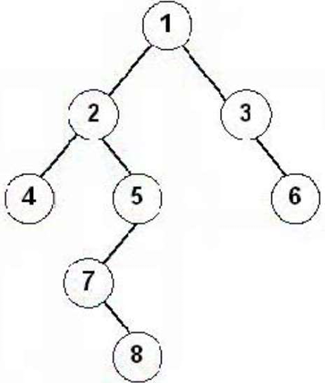
示例：前序:12457836中序:42785136后序:48752631

层次遍历：按层次，从上到下，从左到右

反向构造二叉树：仅仅有前序和后序是无法构造二叉树的，必须要是和中序遍历的集合才能反向构造出二叉树。构造时，前序和后序遍历可以确定根节点，中序遍历用来确定根节点的左子树节点和右子树节点，而后按此方法进行递归，直至得出结果。

实战演练

对于下面二叉树,按中序遍历所得的节点序列为()，节点2的度为()。

A 1234567 B 1247356 C 7425631 D 4721536

A 0 B 1 C 2 D 3

正确答案:D B 答案解析: 常用的遍历方法有：前序--先访问根节点，然后从左到右遍历根节点的各棵子树，后序--先从左到右谝历根节点的各棵子树，然后访问根节点，层序--先访问处于第1层上的节点，然后从左到右依次访问处于第2层、3层上的节点，即自上而下、自左至右逐层访问树各层上的节点。该二叉树前序遍历次序为1247356，中序遍历次序为4721536，后序遍历次序为7425631，层序遍历次序为1234567。节点的度是指其子树的个数。节点2只有左子树，故其度为1。

任何一棵二叉树的叶结点在前序、中序、后序序列中的相对次序()

A 不发生改变 B 发生改变 C 不能确定 D 以上都不对

正确答案:A 答案解析: 任何一颗二又树的叶子结点在先序、中序、后序遍历序列中的相对次序是不发生改变的，因为根据三个遍历的次序和特点:前序是根左右、中序是左根右、后序是左右根,因此相对次序发生变化的都是子树的根,也就是分支结点。

已知一棵二叉树的后序遍历为DABEC，中序遍历为DEBAC，则先序遍历为()。

A ACBED B DECAB C DEABC D CEDBA

正确答案:D 根据后序遍历与中序遍历可以构造出二叉树，如下图所示，由图可知先序遍历为CEDBA。

已知一棵二叉树的先序遍历结果为ABCDEF，中序遍历结果为CBAEDF，则后序遍历结果为()。

A CBEFDA B FEDCBA C CBEDFA D 不确定

正确答案:A 根据先序遍历和中序遍历构造二叉树如下，在进行后序遍历为A.

某二叉树的先序遍历序列为cabfedg,中序遍历序列为abcdefg,则该二叉树是() A 完全二叉树 B 最优二叉树 C 平衡二叉树 D 满二叉树 正确答案:C 本题考查数据结构基础知识。二叉树的遍历主要有四种:前序遍历(先根遍历、先序遍历):遵循“根-左.右”的递归遍历思想，根一定是当前子二又树先序遍历序列的第一个元素:中序遍历(中根遍历):遵循“左-根-右”的递归遍历思想，根位于是当前子二叉树中序遍历序列的中部位置，左边是当前根的左二叉树，右边是当前根的右二叉树;后序遍历(后根遍历):遵循“左-右-根”的递归遍历思想，根一定是遍历序列的最后一个元素;层次遍历:遵循从上到下，直左而右的遍历思想，根一定是遍历序列的第一个元素。根据题意，本二又树为:

平衡二叉树或者是一棵空树，或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。本题的二叉树满足平衡二叉树的特点要求，故选择C

若某二叉树的后序遍历序列为KBFDCAE，中序遍历序列为BKEFACD，则该二叉树为().

正确答案:A 依题意，选项A的二又树，其中序遍历序列为BKEFACD，后序遍历序列为KBFDCAE.

当一棵非空二叉树的()时，对该二叉树进行中序遍历和后序遍历所得 的序列相同。 A 每个非叶子结点都只有左子树 B 每个非叶子结点都只有右子树 C 每个非叶子结点的度都为1 D 每个非叶子结点的度都为2 正确答案:A答案解析: 中序遍历的顺序是左根右，后序遍历的顺序是左右根，若每个非叶子节点都只有左子树，那中序后序的遍历顺序此时可以简单的看成是左根，二者的序列一致，因此答案选择A选项。

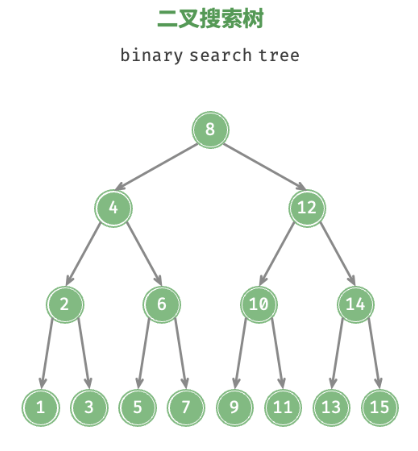
二叉搜索树

如图 7-16 所示，二叉搜索树（binary search tree）满足以下条件。

1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。

2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

二叉搜索树的操作

我们将二叉搜索树封装为一个类 BinarySearchTree ，并声明一个成员变量 root ，指向树的根节点。

1. 查找节点

给定目标节点值 num ，可以根据二叉搜索树的性质来查找。如图 7-17 所示，我们声明一个节点 cur ，从二叉树的根节点 root 出发，循环比较节点值 cur.val 和 num 之间的大小关系。

• 若 cur.val < num ，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right 。

• 若 cur.val > num ，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left 。

• 若 cur.val = num ，说明找到目标节点，跳出循环并返回该节点。

二叉搜索树的查找操作与二分查找算法的工作原理一致，都是每轮排除一半情况。循环次数最多为二叉树的高度，当二叉树平衡时，使用 O(log⁡n) 时间。示例代码如下：

2. 插入节点

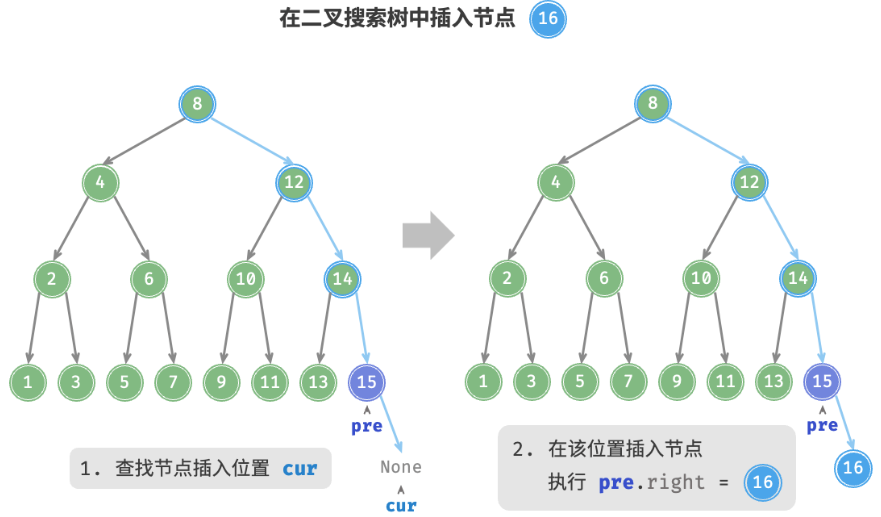
给定一个待插入元素 num ，为了保持二叉搜索树“左子树 < 根节点 < 右子树”的性质，插入操作流程如图 7-18 所示。

1. 查找插入位置：与查找操作相似，从根节点出发，根据当前节点值和 num 的大小关系循环向下搜索，直到越过叶节点（遍历至 None ）时跳出循环。

2. 在该位置插入节点：初始化节点 num ，将该节点置于 None 的位置。

在代码实现中，需要注意以下两点。

• 二叉搜索树不允许存在重复节点，否则将违反其定义。因此，若待插入节点在树中已存在，则不执行插入，直接返回。

• 为了实现插入节点，我们需要借助节点 pre 保存上一轮循环的节点。这样在遍历至 None 时，我们可以获取到其父节点，从而完成节点插入操作。

与查找节点相同，插入节点使用 O(log⁡n) 时间。

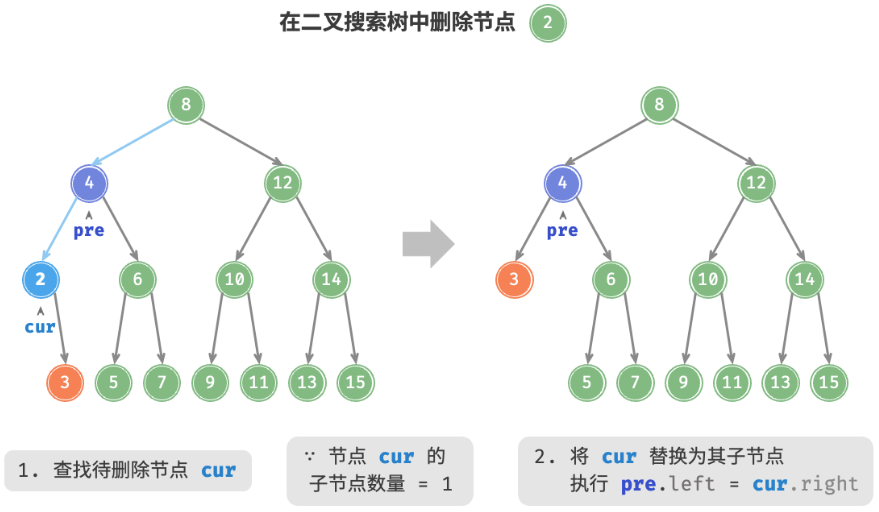
3. 删除节点

先在二叉树中查找到目标节点，再将其删除。与插入节点类似，我们需要保证在删除操作完成后，二叉搜索树的“左子树 < 根节点 < 右子树”的性质仍然满足。因此，我们根据目标节点的子节点数量，分 0、1 和 2 三种情况，执行对应的删除节点操作。如图 7-19 所示，当待删除节点的度为 0 时，表示该节点是叶节点，可以直接删除。

如图 7-20 所示，当待删除节点的度为 1 时，将待删除节点替换为其子节点即可。

当待删除节点的度为 2 时，我们无法直接删除它，而需要使用一个节点替换该节点。由于要保持二叉搜索树“左子树 < 根节点 < 右子树”的性质，因此这个节点可以是右子树的最小节点或左子树的最大节点。

假设我们选择右子树的最小节点（中序遍历的下一个节点），则删除操作流程如图 7-21 所示。

1. 找到待删除节点在“中序遍历序列”中的下一个节点，记为 tmp 。

2. 用 tmp 的值覆盖待删除节点的值，并在树中递归删除节点 tmp 。

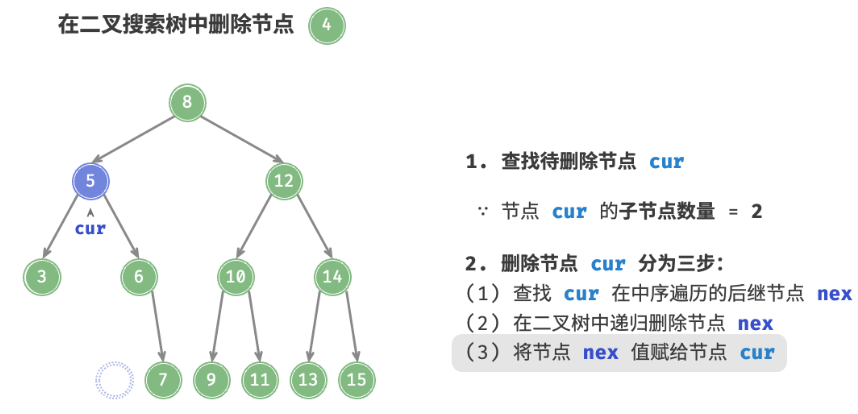
删除节点操作同样使用 O(log⁡n) 时间，其中查找待删除节点需要 O(log⁡n) 时间，获取中序遍历后继节点需要 O(log⁡n) 时间。

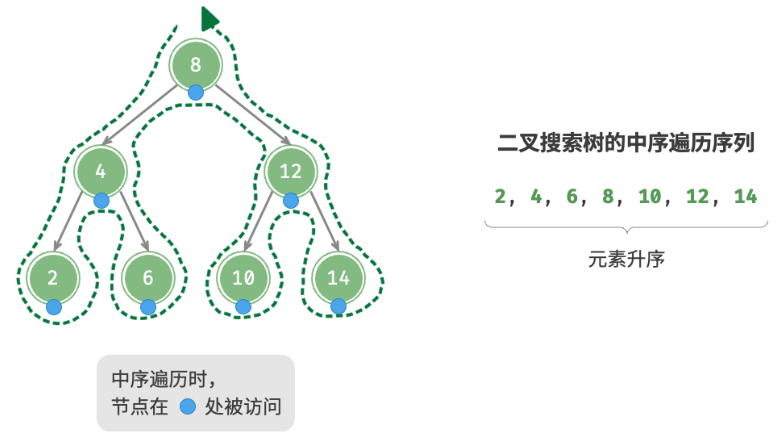
4. 中序遍历有序

如图 7-22 所示，二叉树的中序遍历遵循“左 → 根 → 右”的遍历顺序，而二叉搜索树满足“左子节点 < 根节点 < 右子节点”的大小关系。

这意味着在二叉搜索树中进行中序遍历时，总是会优先遍历下一个最小节点，从而得出一个重要性质：二叉搜索树的中序遍历序列是升序的。

利用中序遍历升序的性质，我们在二叉搜索树中获取有序数据仅需 O(n) 时间，无须进行额外的排序操作，非常高效。

二叉搜索树的效率

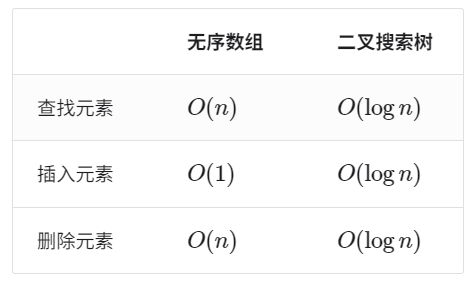
给定一组数据，我们考虑使用数组或二叉搜索树存储。观察表 7-2 ，二叉搜索树的各项操作的时间复杂度都是对数阶，具有稳定且高效的性能。只有在高频添加、低频查找删除数据的场景下，数组比二叉搜索树的效率更高。

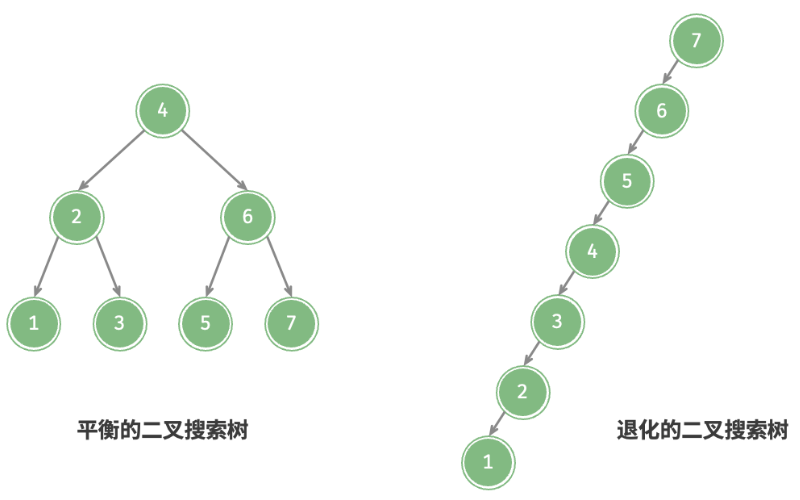
在理想情况下，二叉搜索树是“平衡”的，这样就可以在 log⁡n 轮循环内查找任意节点。

然而，如果我们在二叉搜索树中不断地插入和删除节点，可能导致二叉树退化为图 7-23 所示的链表，这时各种操作的时间复杂度也会退化为 O(n) 。

哈夫曼树⭐

基本概念

最优二叉树又称为哈夫曼树，是一类带权路径长度最短的树，相关概念如下

路径：树中一个结点到另一个结点之间的通路

结点的路径长度：路径上的分支数目。

树的路径长度：根节点到达每一个叶子节点之间的路径长度之和。权:节点代表的值

结点的带权路径长度：该结点到根结点之间的路径长度乘以该节点的权值

树的带权路径长度(树的代价)：树的所有叶子节点的带权路径长度之和

哈夫曼树的求法：给出一组权值，将其中两个最小的权值作为子节点，其和作为父节点，组成二叉树，而后删除这两个叶子节点权值，并将父节点的值添加到该组权值中。重复进行上述步骤，直至所有权值都被使用完。

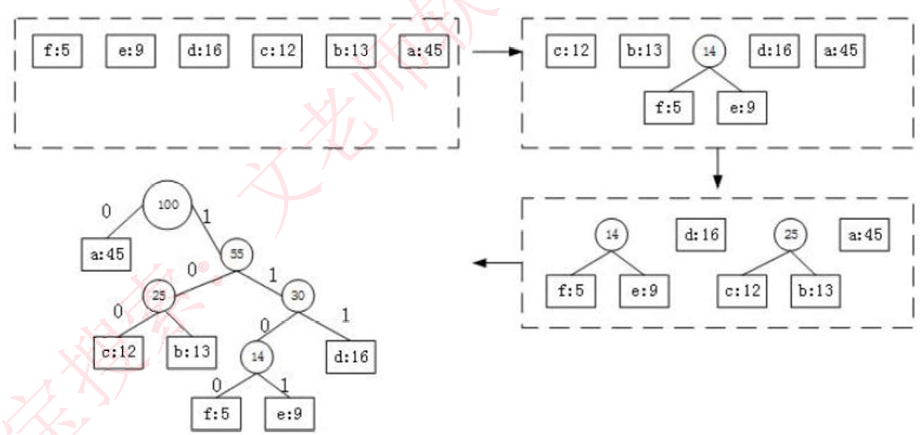
若需要构造哈夫曼编码(要保证左节点值小于右节点的值，才是标准的哈夫曼树)，将标准哈夫曼树的左分支设为0，右分支设为1，写出每个叶节点的编码，会发现，哈夫曼编码前缀不同，因此不会混淆，同时也是最优编码。

实战演练

以下关于 Huffman(哈夫曼)树的叙述中，错误的是()。

A 权值越大的叶子离根结点越近 B Huffman(哈夫曼)树中不存在只有一个子树的结点 C Huffman(哈夫曼)树中的结点总数一定为奇数 D 权值相同的结点到树根的路径长度一定相同

正确答案:D 答案解析: 哈夫曼树又称为最优二叉树，是一种带权路径长度最短的二叉树。树的带权路径长度 也就是树中所有的叶节点得权值乘上其道根节点的路径长度。哈夫曼树的特点是，没有度 为1的节点。n个叶子结点的哈夫曼树，度数为 2 的节点数为 n-1 个，所以，哈夫曼树一共 有 2n-1 个节点。选项 A,B,C的描述都是正确的。

由权值为9，2，5，7的四个叶子结点构造一棵哈夫曼树，该树的带权路径长度为()。

A 23 B 37 C 44 D 46

正确答案:C 根据哈夫曼算法，由权值为9，2，5，7的四个叶子结点构造的一棵哈夫曼树如下图所示。

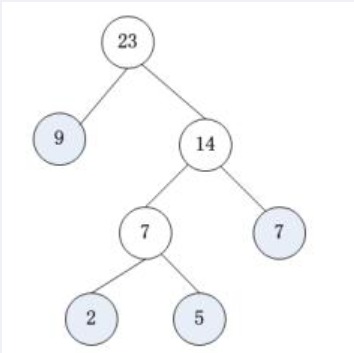
该树的带权路径长度为:9x1+2x3+5x3+7x2=44

已知一个文件中出现的各个字符及其对应的频率如下表所示。若采用定长编码，则该文件中字符的码长应为若采用Huffman编码，则字符序列“bee”的编码应为()。

A 6 B 5 C 4 D 3

A 01011011101 B10011011101 C 10111011101 D010111101011

正确答案:D C ① 有6个不同字母，需要采用3位二进制进行编码。② 本题对应的哈夫曼树如下所示:

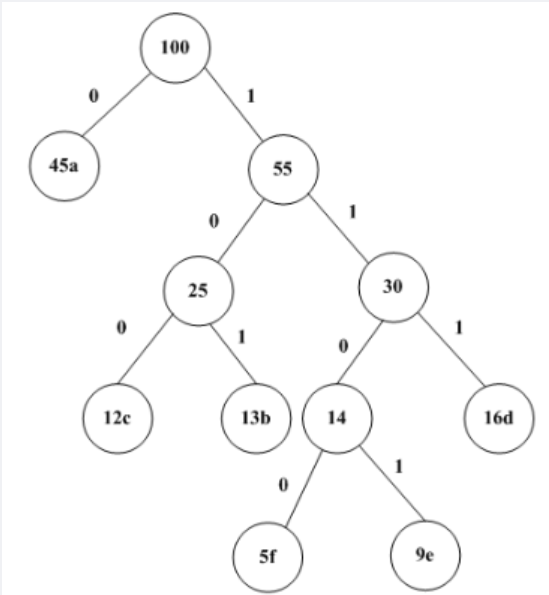
已知一个文件中出现的各字符及其对应的频率如下表所示。采用Huffman 编码，则该文件中字符a和c的码长分别为()。若采用Huffman编码，则字符序列110001001101”的编码应为()。

A 1和3 B 1和4 C 3和3 D 3和4

A face B bace C acde D fade

正确答案:A A根据题意构造哈夫曼树如下。答案解析: 6个字符的编码分别是: a:0,b:101,c:100,d:111,e:1101,f:1100

已知字符集(a,b,c,d,e,f}，若各字符出现的次数分别为6,3,8,2,10,4，则对应字符集中各字符的哈夫曼编码可能为()。 A 00,1011,01,1010,11,100 B 11,100,110,000,0010,01 C 10,1011,11,0011,00,010 D 0011,10,11,0010,01,000

正确答案:A 结合题意构造哈夫曼树如下图所示，在进行左子树为0，右子树为1,进行编码，最后为A

一棵哈夫曼树共有215个结点，对其进行哈夫曼编码，共能得到()个不同的码字。 A 107 B 108 C 214 D 215 正确答案:B 根据哈夫曼树构造过程可知，哈夫曼树中只有度为0和度为2的结点，在非空二叉树中，n0=n2+1。根据此答案解析:关系，n=n0+n2=2n0-1=215,所以n0=108

一棵哈夫曼树共有127个结点，对其进行哈夫曼编码，共能得到()个 字符的编码。 A 64 B 127 C 63 D 126

正确答案:A 答案解析:当两个字符构造哈夫曼树，就会多出一个节点，若是三个字符则多出两个节点，若是四个字符则多出三个节点，以此类推，若是有n个字符构造哈夫曼数，则会多出n-1个节点。因此哈夫曼树的节点数就是n+n-1个,由此计算出字符数为64.

给定整数集合{3,5,8,9,12}，与之对应的哈夫曼树是()。

正确答案: C 答案解析:首先，3和5构造为一棵子树，其跟权值为8，然后该子树与8构造一棵新子树，根权值为16，再后9与12构造为一棵子树，最后两棵子树共同构造为一棵哈夫曼树。

霍夫曼编码将频繁出现的字符采用短编码，出现频率较低的字符采用长编码。具体的操作过程为:i)以每个字符的出现频率作为关键字构建最小优先级队列;ii)取出关键字最小的两个结点生成子树，根节点的关键字为孩子节点关键字之和，并将根节点插入到最小优先级队列中，直至得到一棵最优编码树。霍夫曼编码方案是基于()策略的。用该方案对包含a到f6个字符的文件进行编码，文件包含100000个字符每个字符的出现频率(用百分比表示)如表1-3所示，则与固定长度编码相比，该编码方案节省了()存储空间。 表1-3 某文件中每个字符出现的频率

A 分治 B 贪心 C 动态规划 D 回溯

A 21% B 27% C18% D 36%

正确答案:B A 答案解析: 依题意，霍大曼编码方案是基于贪心策略的。用该方案对包含a~f6个字符的文件进行编码，文件包含100000个字符，每个字符的出现频率(用百分比表示)如表1-3所示，则与固定长度编码相比，该编码方案节省了21%的存储空间。

设有5个字符，根据其使用频率为其构造哈夫曼编码。以下编码方案中，()是不可能的。 A {111，110，101，100,0} B {0000, 0001,001,01,1} C {11,10,01,001,000} D {11,10，011，010,000}答案:D

二叉查找树

查找二叉树上的每个节点都存储一个值，且每个节点的所有左孩子结点值都小于父节点值，而所有右孩子结点值都大于父节点值，是一个有规律排列的叉树，这种数据结构可以方便查找、插入等数据操作。

二叉排序树的查找效率取决于二叉排序树的深度，对于结点个数相同的二叉排序树，平衡二叉树的深度最小，而单枝树的深度是最大的，故效率最差

二叉排序树中进行查找的效率与()有关。

A 二叉排序树的深度 B 二叉排序树的结点个数 C 被查找结点的度 D 二叉排序树的存储结构

正确答案:A 二又排序树的查找路径是自顶向下的，平均查找长度取决于树的高度。

设有二叉排序树(或二叉查找树)如下图所示，建立该二叉树的关键码序列不可能是() A 23 31 17 19 11 27 13 90 61 B 23 17 19 31 27 90 61 11 13 C 23 17 27 19 31 13 11 90 61 D 23 31 90 61 27 17 19 11 13 正确答案:C 二叉查找树(又称二叉搜索树，二叉排序树)它或者是一棵空树，或者是具有下列性质的二叉树: 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值: 它的左、右子树也分别为二叉排序树。31是27的父亲节点，31必须在27前面：构建树的方法：第一个元素为根节点，然后依次按照左子树小于根节点，右子树大于根节点的方法添加即可

平衡二叉树

基本概念

平衡二叉树又称为AVL树，它或者是一棵空树，或者是具有下列性质的二叉树它的左子树和右子树都是平衡二又树，且左子树和右子树的高度之差的绝对值不超过1。若将二叉树结点的平衡因子(Balance Factor，BF)定义为该结点左于树的高度减去其右子树的高度，则平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

实战演练

在平衡二叉排序树上进行查找时，其时间复杂度为()

A O(log2n+1) B O(log2n) C O(log2n-1) D log22n

正确答案:B 答案解析:此题是考查二叉树的查找效率问题。这是二叉树的基本查找问题，因为是平衡二叉树，其时间复杂度即为树的高，所以为log2n。

完全二叉树

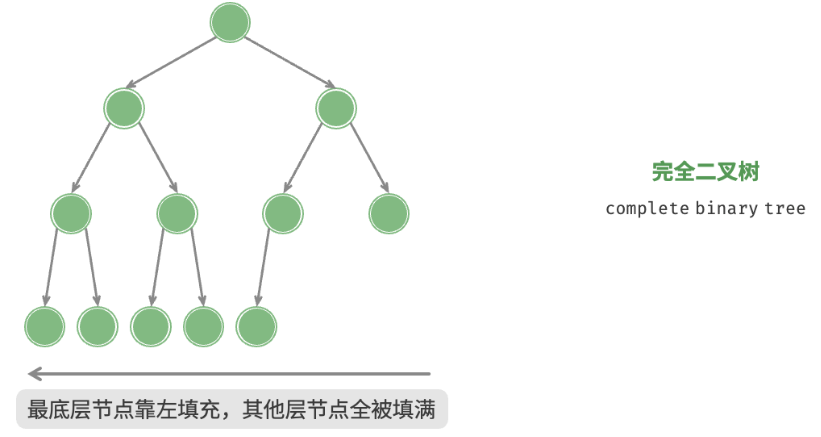
完全二叉树（complete binary tree）只有最底层的节点未被填满，且最底层节点尽量靠左填充。

当二叉树的结点数目确定时，()的高度一定是最小的。

A 二叉排序树 B 完全二叉树 C 线索二叉树 D 最优二叉树

正确答案:B 答案解析: 完全二又树同样层数的结点最多，因此高度最小。

在()中，任意一个结点的左、右子树的高度之差的绝对值不超过1。

A 完全二叉树 B 二叉排序树 C 线索二叉树 D 最优二叉树

正确答案:A V本颖考查二叉树的基本概念。在平衡二叉树中，任意一个结点的左、右子树的高度之差的绝对值不超过1。虽然在结构上都符合二叉树的定义，但完全二叉树、线索二叉树、二叉排序树与最优二叉树的应用场合和概念都不同。线索二又树与二又树的遍历运算相关，是一种存储结构。二叉排序树的结构与给定的初始关键码序列相关。最优二叉树(即哈夫曼树)是一类带权路径长度最短的二叉树，由给定的一个权值序列构造线索二叉树、二又排序树和最优二又树在结构上都不要求是平衡二又树。在完全二叉树中，去掉最后一层后就是满二叉树，而且最后一层上的叶子结点必须从该层的最左边开始排列，满足任意一个结点的左、右子树的高度之差的绝对值不超过1的条件，因此在形态上是一个平衡的二叉树。

重点回顾

• 二叉树是一种非线性数据结构，体现“一分为二”的分治逻辑。每个二叉树节点包含一个值以及两个指针，分别指向其左子节点和右子节点。

• 对于二叉树中的某个节点，其左（右）子节点及其以下形成的树被称为该节点的左（右）子树。

• 二叉树的相关术语包括根节点、叶节点、层、度、边、高度和深度等。

• 二叉树的初始化、节点插入和节点删除操作与链表操作方法类似。

• 常见的二叉树类型有完美二叉树、完全二叉树、完满二叉树和平衡二叉树。完美二叉树是最理想的状态，而链表是退化后的最差状态。

• 二叉树可以用数组表示，方法是将节点值和空位按层序遍历顺序排列，并根据父节点与子节点之间的索引映射关系来实现指针。

• 二叉树的层序遍历是一种广度优先搜索方法，它体现了“一圈一圈向外扩展”的逐层遍历方式，通常通过队列来实现。

• 前序、中序、后序遍历皆属于深度优先搜索，它们体现了“先走到尽头，再回溯继续”的遍历方式，通常使用递归来实现。

• 二叉搜索树是一种高效的元素查找数据结构，其查找、插入和删除操作的时间复杂度均为 O(log⁡n) 。当二叉搜索树退化为链表时，各项时间复杂度会劣化至 O(n) 。

• AVL 树，也称平衡二叉搜索树，它通过旋转操作确保在不断插入和删除节点后树仍然保持平衡。

• AVL 树的旋转操作包括右旋、左旋、先右旋再左旋、先左旋再右旋。在插入或删除节点后，AVL 树会从底向顶执行旋转操作，使树重新恢复平衡。

查找⭐

顺序查找

顺序查找的思想：将待查找的关键字为key的元素从头到尾与表中元素进行比较，如果中间存在关键字为key的元素，则返回成功;否则，则查找失败。平均查找长度为：时间复杂度为O(n)。

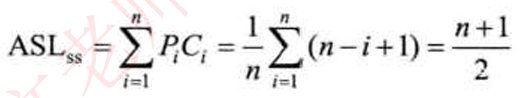
折半查找

二分查找（binary search）是一种基于分治策略的高效搜索算法。它利用数据的有序性，每轮缩小一半搜索范围，直至找到目标元素或搜索区间为空为止。

先初始化指针 i=0 和 j=n−1 ，分别指向数组首元素和尾元素，代表搜索区间 [0,n−1] 。请注意，中括号表示闭区间，其包含边界值本身。下来，循环执行以下两步。

1. 计算中点索引 m=⌊(i+j)/2⌋ ，其中 ⌊ ⌋ 表示向下取整操作。

2. 判断 nums[m] 和 target 的大小关系，分为以下三种情况。

   1. 当 nums[m] < target 时，说明 target 在区间 [m+1,j] 中，因此执行 i=m+1 。

   2. 当 nums[m] > target 时，说明 target 在区间 [i,m−1] 中，因此执行 j=m−1 。

   3. 当 nums[m] = target 时，说明找到 target ，因此返回索引 m 。

若数组不包含目标元素，搜索区间最终会缩小为空。此时返回 −1 。值得注意的是，由于 i 和 j 都是 int 类型，因此 i+j 可能会超出 int 类型的取值范围。为了避免大数越界，我们通常采用公式 m=⌊i+(j−i)/2⌋ 来计算中点。

实现二分查找(折半查找)时，要求查找表(55)

A 顺序存储，关键码无序排列 B 顺序存储，关键码有序排列 C 双向链表存储，关键码无序排列 D 双向链表存储，关键码有序排列

正确答案:B 答案解析:二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好:其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。分查找算法要求:①必须采用顺序存储结构;②必须按关键字大小有序排列。

在有11个元素的有序表A[1,2,3…11]中进行折半查找，向下取整，查找元素A时[11]，被比较的元素下标依次是()。 6 8 10 11 6 9 10 11 6 7 9 11 6 8 9 11

正确答案:B 答案解析: 根据折半查找思想，第一次mid=(1+11)/2=6，第二次mid=(7+11)/2=9,第三次mid=(10+11)/2=10，第四次mid=11。

已知一个有序表13,18,24,35,47,50,62,83,90,115,134,当二分查找值为90，查找成功的比较次数为()。

A 1 B 2 C 4 D 6

正确答案:B 答案解析: 开始时low指向13，high指向134，mid指向50，比较第一次90>50,所以将low指向62，high指向134mid指向90，第二次比较找到90。

对长度为n的有序顺序进行折半查找(即二分查找)的过程可用一棵判定树表该判定树的形态符合()的特点

A 最优二叉树(即哈夫曼树) B 平衡二叉树 C 完全二叉树 D 最小生成树 正确答案:B

在13个元素构成的有序表A[1..13]中进行折半查找(或称为二分查找，向下取整)。那么以下叙述中，错误的是()。

无论要查找哪个元素，都是先与A[7]进行比较

若要查找的元素等于A[9]，则分别需与A[7]、A[11]、A[9]进行比较

无论要查找的元素是否在A[]中，最多与表中的4个元素比较即可

若待查找的元素不在A[]中，最少需要与表中的3个元素进行比较

正确答案:B答案解析 : 考察数据结构折半査找算法，B选项错误之处在于，要査找a[9]元素，第一次比较的是A[7](下标计算方法为:[1+13]/2=7)，第2次比较的是A[10](下标计算方法为:[8+13]/2=10)。

对于关键字序列(26，25，72，38，8，18，59)，采用散列函数H(Key)=Key mod 13构造散列表(哈希表)。若采用线性探测的开放定址法解决冲突(顺序地探查可用存储单元)，则关键字59所在散列表中的地址为

正确答案:D 答案解析:本题考查散列表的基本概念。对于关键字序列(26，25，72，38，8，18，59)和散列函数H(Key)=Key mod 13，采用线性探测的开放定址法解决冲突构造的散列表如下表所示:

在13个元素构成的有序表M[1...13]中进行折半查找(向下取整)，若找到的元素为M[4]，则被比较的元素依次为()。

A M[7]、M[3]、M[5]、M[4] B M[7]、M[5]、M[4] C M[7]、M[6]、M[4] D M[7]、M[4] 正确答案:A 答案解析: 在13个元素构成的有序表M[1..13]中进行折半查找(向下取整)，若找到的元素为M[4]，则被比较的元素依次为M[71、M[3]、M[5]、M[4]

对某有序概序表进行折率查找《二分查找》 时，进行比较的关键字序列不可能是()

42,61,90,85,77 42,90.85,61,77 90,85,61,77,42 90,85,77,61.42

正确答案：C

对某有序表进行二分查找时，进行比较的关键字序列不可能是( 60)

42,61,90,85,77 42,90.85,61,77 90,85,61,77,42 90,85,77,61,42

正确答案:C，答案解析:分查找的前提是元素有序(一般是升序)，基本思想是拿中间元素。A[m]与要查找的元素x进行比较，如果相等，则已经找到，如果A[m]比x大，那么要找的元素一定在A[m]前边(左边)，如果A[m]比x小，那么要找的元素一定在A[m]后边(右边)。每进行一次查找，数组规模减半。反复将子数组规模减半，直到发现要查找的元素，或者当前子数组为空。选项C错在如果一个元素比61大，下一次可以跟77比较，但是77后面的元素是42，说明要查找的元素比77小，因此再次比较确实是跟42 比，而题于已经表明这个元素大于61了，明显不合理。因此答案选C。

以下关于折半查找的叙述中，不正确的是()。采用折半查找等概率查找某个包含8个元素的有序表，查找成功的平均查找长度为()。请回答第1个问题 是一个分治算法

只能应用于有序表

查找成功和不成功的平均查找长度是一样的

若表长为n, 时间复杂度为0(logn)

正确答案:C 答案解析 : 折半查找是在有序数组中查找特定元素，将数组分成两半，若中间元素不是特定元素，则将其中一半的数据再分成两半，直至找到特定元素，符合分治算法的基本思想。因此A、B选项正确。查找成功的平均长度是将每个元素的查找次数相加后再除以元素总数，而查找不成功则是最后的结果是空指针，因此需要算出每个空指针的查找次数再累加后除以空指针总数，它们的平均查找长度不一定相同。因此C选项错误，若表长为n,则时间复杂度为O(log n),D选项正确,

以下关于折半查找的叙述中，不正确的是()。采用折半查找等概率查 找某个包含8个元素的有序表，查找成功的平均查找长度为()。请回答第2个问题

9/8 1/8 20/8 21/8

正确答案:D 答案解析:查找成功的平均长度是将每个元素的查找次数相加后再除以元素总数。8个元素，能一次命中的有1个元素2次查找命中的有2个元素，3次查找命中的有4个元素，4次才能命中的有1个元素。所以平均长度是(1+2*2+3*4+4)/8=21/8.

在29个元素构成的查找表中查找任意一个元素时，可保证最多与表中5个元素进行比较即可确定查找结果，则采用的查找表及查找方法是()。

A 二叉排序树上的查找 B 顺序表上的顺序查找

C 有序顺序表上的二分查找 D 散列表中的哈希查找

正确答案:C 答案解析: 由29个元素构成的有序顺序表，采用二分查找，二分查找的决策树深度为log229向上取整为5，比较次数最多达5次。采用二又排序树查找，若二叉排序树为单支树，则比较次数最多可达29次。采用顺序表进行顺序查找，比较次数最多也可达29次。若采用散列表中的哈希查找，在前28个地址都满的情况下，在进行最后个函数值的哈希值为0，则需从头开始比较到最后一个位置，因此比较次数最多可达29次。

在13个元素构成的有序表M[1..13]中进行折半查找(向下取整)，若找到的为M[4]，则被比较的元素依次为

A.M[7]、M[3]、M[5]、M[4] B.M[7]、M[5]、M[4] C.M[7]、M[6]、M[4] D.M[7]、M[4] 答案:A

哈希查找

哈希表（hash table），又称散列表，它通过建立键 key 与值 value 之间的映射，实现高效的元素查询。具体而言，我们向哈希表中输入一个键 key ，则可以在 O(1) 时间内获取对应的值 value 。

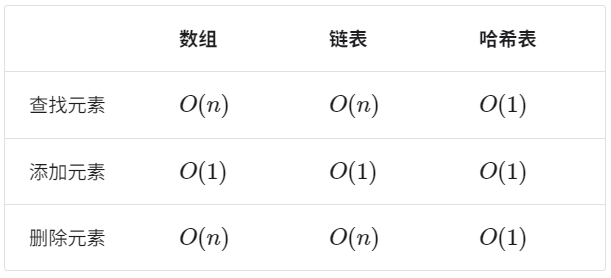
哈希表通过一个以记录的关键字为自变量的函数(称为哈希函数)得到该记录的存储地址，所以在哈希表中进行查找操作时，需要用同一哈希函数计算得到待查记录的存储地址，然后到相应的存储单元去获得有关信息再判定查找是否成功。

例如，设关键码序列为“47，34，13，12，52，38，33，27，3”，哈希表表长为11，哈希函数为 Hash(key)=key mod 11，则Hash(47)=47 MOD 11=3,Hash(34)=34 MOD 11 = 1,Hash(13)=13 MOD 11 =2, Hash(12)=12 MOD 11 = 1,Hash(52)=52 MOD 11=8, Hash(38)=38 MOD 11 = 5,Hash(33)=33 MOD 11 =0, Hash(27)= 27 MOD 11 =5,Hash(3)=3 MOD 11 =3. 使用线性探测法解决冲突构造的哈希表如下:

哈希函数产生了冲突的解决方法如下

1. 开放定址法：Hi=(H(key)+di)% m i=1,2,.., k(k≤m-1)其中，H(key)为哈希函数;m为哈希表表长;di为增量序列：常见的增量序列有以下3种。

1. 链地址法：它在查找表的每一个记录中增加一个链域，链域中存放下一个具有相同哈希函数值的记录的存储地址。利用链域，就把若干个发生冲突的记录链接在一个链表内。当链域的值为NULL时，表示已没有后继记录了。因此，对于发生冲突时的查找和插入操作就跟线性表一样了。

2. 再哈希法：在同义词发生地址冲突时计算另一个哈希函数地址，直到冲突不再发生。这种方法不易产生聚集现象，但增加了计算时间。

3. 建立一个公共溢出区：无论由哈希函数得到的哈希地址是什么，一旦发生冲突都填入到公共溢出区中。

已知有序数组a的前10000个元素是随机整数，现需查找某个整数是否在该数,中。以下方法中，()的查找效率最高。A二分查找法 B顺序查找法 C逆序查找法 D哈希查找法

正确答案:D，答案解析: 哈希算法是使用给定数据构造哈希表，然后在哈希表上进行查找的一种算法。先给定一个值，然后根据哈希函数求得哈希地址，再根据哈希地址查找到要找的元素。是通过数据元素的存储地地进行查找的一种算法。哈希表运算得非常快，在计算机程序中，如果需要在一秒种内查找上千条记录通常使用哈希表(例如拼写检查器)哈希表的速度明显比树快，树的操作通常需要O(N)的时间级。哈希表不仅速度快，编程实现也相对容易

对于关键字序列(10,34,37， 51,14,25，56,22,3),用线性探查法解决冲突构造哈希表，哈希函数为H(key)=key%11,关键字25存入的哈希地址编号为()。A 2 B 3 C 5 D 6

正确答案:C根据题中给出的散列函数，对关键字序列计算其散列地址，如下:H(10)=10%11=10 H(34)=34%11=1 H(37)=37%11=4 H(51)=51%11=7 H(14)=14%11=3 H(25)=25%11=3，但是地址3已经放入了14，发生冲突，向后探测一步，地址4内存37，继续向后探测一步，地址5为空，将25放入地址5。

设用线性探查法解决冲突构造哈希表，且哈希函数为H(key)=key%m，若在该哈希表中查找某关键字e是成功的且与多个关键字进行了比较，则()。

A 这些关键字形成一个有序序列 B 这些关键字都不是e的同义词

C 这些关键字都是e的同义词 D 这些关键字的第一个可以不是e的同义词

正确答案:D答案解析: 同义词才会占用同个位置，从而需要进行多次比较。这些关键字的第一个可以不是e的同义词，可以是排在e之前的关键字正好占了那个位置。

设散列表长m=14,散列函数为H(key)=key%11，表中仅有4个结点H()=4，H()=5，H()=6，H()=7，若使用线性探测法处理冲突，则关键字49存储的地址是()。A 3 B 5 C 8 D 9 正确答案:C

答案解析：49%11=5.发生冲突 线性探测6，发生冲突 线性探测7发生冲突 线性探测8 无冲突

一组记录的关键为19,14,23,1,68,20,84,27,55,11,10,79，用链地址法构造散列表，散列函数为H(key)=key MOD 13，散列地址为1的链中有()个记录。A 1 B 2 C 3 D 4

正确答案:D、答案解析 : 根据散列函数计算可知，14,1,27,79散列后的地址都是1，所以有4个记录。

一组记录的关键为19,14,23,1,68,20,84,27,55,11,10,79，用链地址法构造散列表，散列函数为H(key)=key MOD 13，散列地址为1的链中有()个记录。A 1 B 2 C 3 D 4

正确答案:D 答案解析: 根据散列函数计算可知，14,1,27,79散列后的地址都是1，所以有4个记录。

以下关于散列表(哈希表)，及其查找特点的叙述中，正确的是

A 在散列表中进行查找时，只需要与待查找关键字及其同义词进行比较

B 只要散列表的装填因子不大于1/2，就能避免冲突

C 用线性探测法解决冲突容易产生聚集问题

D 用链地址法解决冲突可确保平均查找长度为1 正确答案:C

用哈希表存储元素时，需要进行冲突(碰撞)处理，冲突是指()。

A 关键字被依次映射到地址编号连续的存储位置 B 关键字不同的元素被映射到相同的存储位置 C 关键字相同的元素被映射到不同的存储位置 D 关键字被映射到哈希表之外的位置

答案:B 构造哈希表时，关键字序列中两个不同的元素被哈希函数映射到同一个哈希单元时，称为冲突

图

基本概念

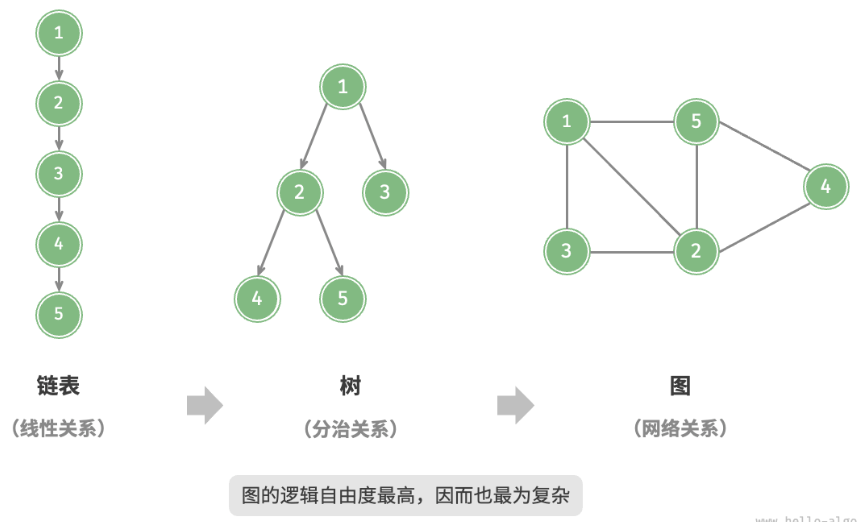
图（graph）是一种非线性数据结构，由顶点（vertex）和边（edge）组成。我们可以将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合。以下示例展示了一个包含 5 个顶点和 7 条边的图。

如果将顶点看作节点，将边看作连接各个节点的引用（指针），我们就可以将图看作一种从链表拓展而来的数据结构。如图 9-1 所示，相较于线性关系（链表）和分治关系（树），网络关系（图）的自由度更高，因而更为复杂。

为了描述n个人之间的同学关系，可用()结构表示。

A 线性表 B 树 C 图 D 队列 正确答案:C 答案解析: 在线性表中，数据元素之间仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继:在树形结构中，数据元素之间有着明显的层次关系，并且每一层上的数据元素可自能和下一层中多个元素有关系，但只能和上一层中一个元素有关系;而在图结构中，结点之间的关系可以是任意的，图中任意两个数据元素之间都可能有关系。在描述n个人之间的同学关系时，使用图这种数据结构表示是较合适的。

无向图和有向图

根据边是否具有方向，可分为无向图（undirected graph）和有向图（directed graph）

• 在无向图中，边表示两顶点之间的“双向”连接关系，例如微信或 QQ 中的“好友关系”。

• 在有向图中，边具有方向性，即 A→B 和 A←B 两个方向的边是相互独立的，例如微博或抖音上的“关注”与“被关注”关系。

一个具有n(n>0)个顶点的无向连通图至少有 ()条边。

A n+1 B n C n/2 D n-1

正确答案:D 答案解析:在无向图中，如果从一个顶点到另一个顶点有路径，则称这两个顶点是连通的。如果对于图中任意两个顶点都是连通的，则称该无向图是连通的。所以具有n(n>0)个顶点的连通无向图至少有n-1条边。

n个顶点的有向完全图中含有向边的数目最多为()。

A n-1 B n C n(n-1)/2 D n(n-1)

正确答案:D 答案解析: n个顶点的有向完全图中，每个顶点都向其他n-1个顶点发出一条弧，因此总的有向边的数目为n(n-1)。

某图G的邻接表中共有奇数个表示边的结点，则图G()

A 有奇数个顶点 B 有偶数个顶点 C 是无向图 D 是有向图 正确答案:D

无向图中一个顶点的度是指图中()

A 通过该顶点的简单路径数 B 通过该顶点的回路数

C 与该顶点相邻接的顶点数 D 与该顶点连通的顶点数 正确答案:C 答案解析: 概念题。无向图中一个顶点的度是指与该顶点相邻接的顶点数

在进行软件开发时，采用无主程序员的开发小组，成员之间相互平等:而主程序员负责制的开发小组，由一个主程序员和若干成员组成，成员之间没有沟通。在一个由9名开发人员构成的小组中，无主程序员组和主程序员组的沟通路径分别是()。 A 32和8 B 32和7 C 36和8 D28和7 正确答案:C 答案解析:无主程序员组沟通渠道=N(N-1)/2=9*8/2=36，其中N是指参加沟通的人数。 主程序员组由于成员之间没有沟通，都与主程序员沟通，所以沟通路径为8。

连通图和非连通图

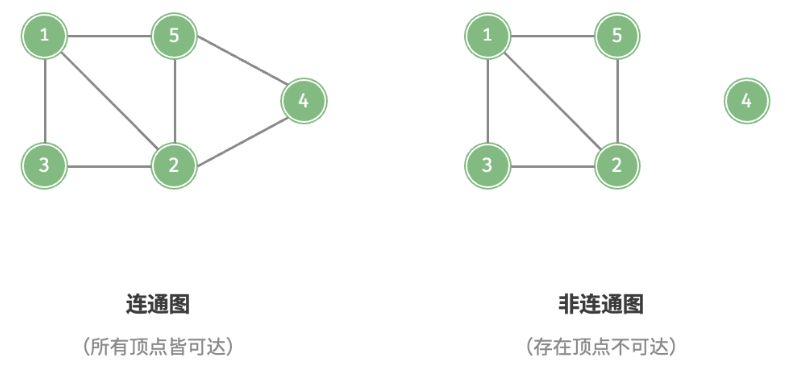
根据所有顶点是否连通，可分为连通图（connected graph）和非连通图（disconnected graph）

• 对于连通图，从某个顶点出发，可以到达其余任意顶点。

• 对于非连通图，从某个顶点出发，至少有一个顶点无法到达。

我们还可以为边添加“权重”变量，从而得到如图 9-4 所示的有权图（weighted graph）。例如在《王者荣耀》等手游中，系统会根据共同游戏时间来计算玩家之间的“亲密度”，这种亲密度网络就可以用有权图来表示。

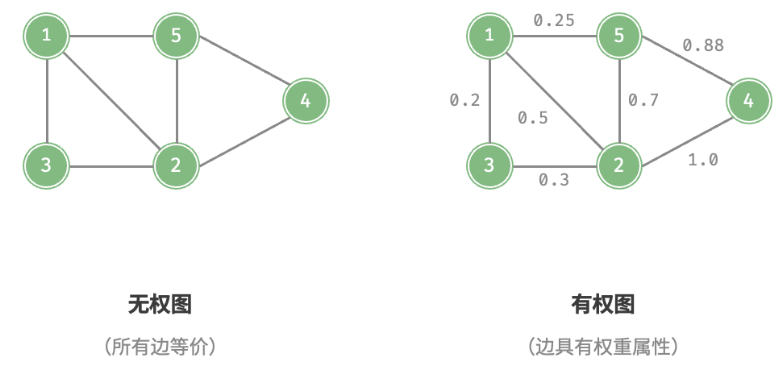
图数据结构包含以下常用术语

• 邻接（adjacency）：当两顶点之间存在边相连时，称这两顶点“邻接”。在图 9-4 中，顶点 1 的邻接顶点为顶点 2、3、5。

• 路径（path）：从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”。在图 9-4 中，边序列 1-5-2-4 是顶点 1 到顶点 4 的一条路径。

• 度（degree）：一个顶点拥有的边数。对于有向图，入度（in-degree）表示有多少条边指向该顶点，出度（out-degree）表示有多少条边从该顶点指出。

由8位成员组成的开发团队中，一共有()条沟通路径

A 64 B 56 C 32 D 28

正确答案:D 答案解析: 沟通路径公式:nx(n-1)/2=8x7/2=28

邻接矩阵和邻接表

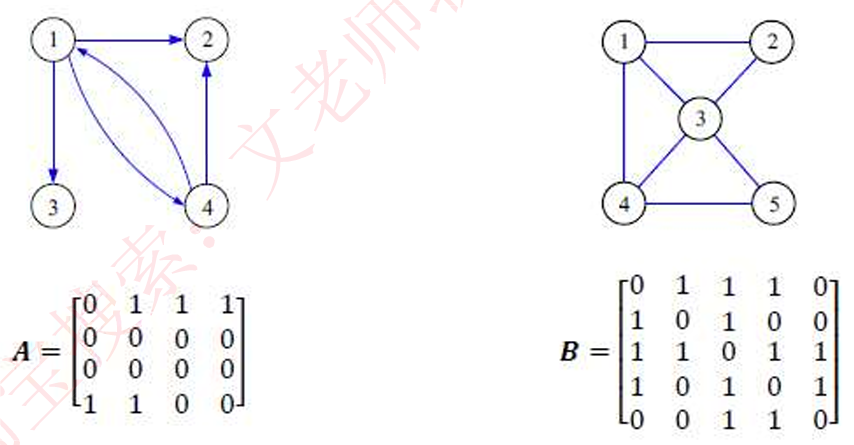
图的基础操作可分为对“边”的操作和对“顶点”的操作。在“邻接矩阵”和“邻接表”两种表示方法

基于邻接矩阵的实现

图的存储邻接矩阵：假设一个图中有n个节点，，则使用n阶矩阵来存储这个图中各节点的关系，规则是若节点i节点i有连线，则矩阵Ri,ji=1，否则为0，示例如下图所示:

基于邻接表的实现

邻接链表：用到了两个数据结构，先用一维数组将图中所有顶点存储起来，而后，对此一维数组的每个顶点元素，使用链表挂上其出度到达的结点的编号和权值，示例如下图所示:

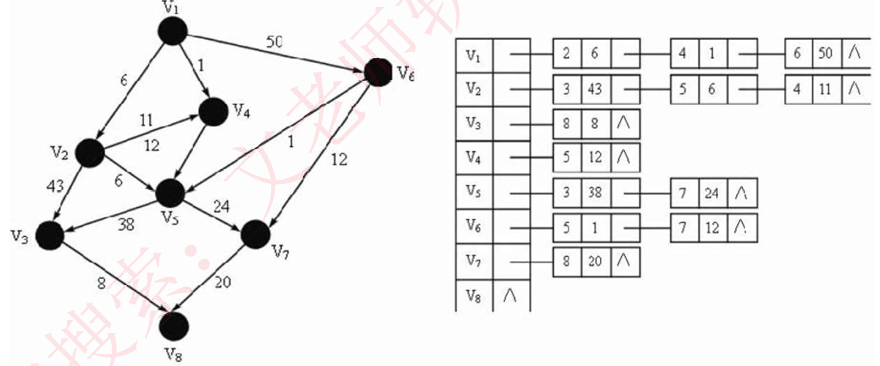
存储特点：图中的顶点数决定了邻接矩阵的阶和邻接表中的单链表数目，边数的多少决定了单链表中的结点数，而不影响邻接矩阵的规模，因此采用何种存储方式与有向图、无向图没有区别，要看图的边数和顶点数，完全图适合采用邻接矩阵存储。

效率对比

设图中共有 n 个顶点和 m 条边，表对比了邻接矩阵和邻接表的时间效率和空间效率。

观察表，似乎邻接表（哈希表）的时间效率与空间效率最优。但实际上，在邻接矩阵中操作边的效率更高，只需一次数组访问或赋值操作即可。综合来看，邻接矩阵体现了“以空间换时间”的原则，而邻接表体现了“以时间换空间”的原则。

下列关于图的存储结构的叙述中，正确的是(). A 一个图的邻接矩阵表示唯一，邻接表表示唯一 B 一个图的邻接矩阵表示不唯一，邻接表表示唯一 C 一个图的邻接矩阵表示唯一，邻接表表示不唯一 D 一个图的邻接矩阵表示不唯一，邻接表表示不唯一

正确答案：C 答案解析:邻接矩阵表示唯一是因为图中边的信息在矩阵中有确定的位置，邻接表不唯一是因为邻接表的建立取决于建立边的顺序和表中的插入算法。

图的遍历

图的遍历是指从图的任意节点出发，沿着某条搜索路径对图中所有节点进行访问且只访问一次

分为以下两种方式：

深度优先遍历：从任一顶点出发，遍历到底，直至返回，再选取任一其他节点出发，重复这个过程直至遍历完整个图;

广度优先遍历：先访问完一个顶点的所有邻接顶点，而后再依次访问其邻接顶点的所有邻接顶点，类似于层次遍历

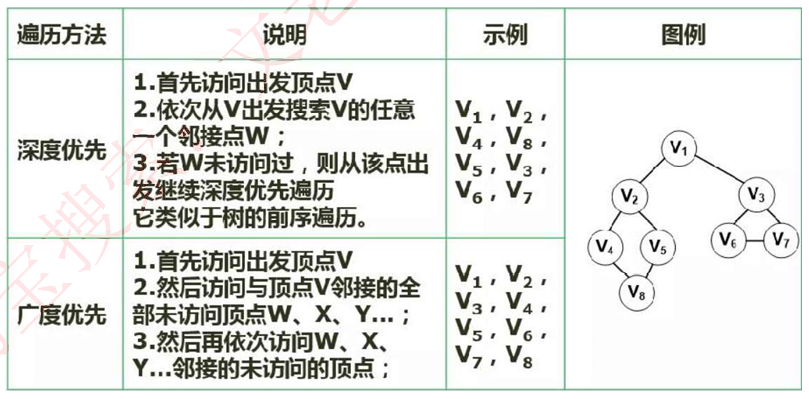
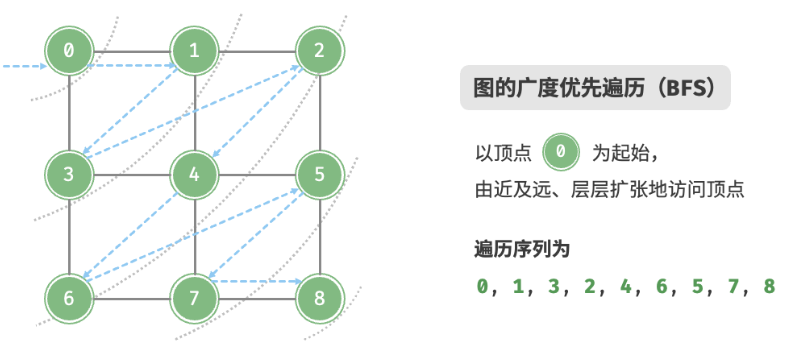
广度优先遍历

广度优先遍历是一种由近及远的遍历方式，从某个节点出发，始终优先访问距离最近的顶点，并一层层向外扩张。从左上角顶点出发，首先遍历该顶点的所有邻接顶点，然后遍历下一个顶点的所有邻接顶点，以此类推，直至所有顶点访问完毕。

深度优先遍历

深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。从左上角顶点出发，访问当前顶点的某个邻接顶点，直到走到尽头时返回，再继续走到尽头并返回，以此类推，直至所有顶点遍历完成。

时间复杂度：所有顶点都会被访问 1 次，使用 O(|V|) 时间；所有边都会被访问 2 次，使用 O(2|E|) 时间；总体使用 O(|V|+|E|) 时间。

空间复杂度：列表 res ，哈希集合 visited 顶点数量最多为 |V| ，递归深度最大为 |V| ，因此使用 O(|V|) 空间。

实战演练

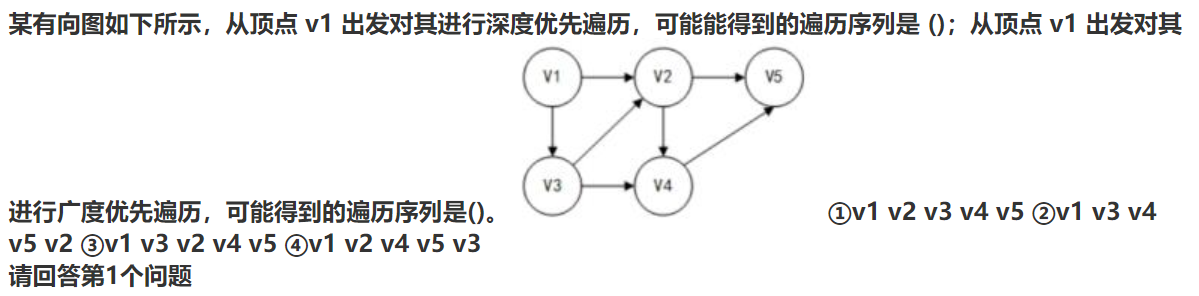
A ①②③ B ①③④ C ①②④ D ②③④

A ①② B ①③ C ②③ D ③④

正确答案:D B 图的深度优先遍历我们可以把他看成树的前序遍历，广度优先遍历可以看成树的层次遍历。由此，我们得出他的深度优先遍历序列是②v1 v3 v4 v5 v2 ③v1 v3 v2 v4 v5 ④ v1 v2 v4 v5 v3 广度优先遍历序列是①v1 v2 v3 v4 v5③v1 v3 v2 v4 v5，因此，答案分别是 D和 B

下列选项中，不是下图深度优先搜索序列的是()

A V1,V5,V4,V3,V2 B V1,V3,V2,V5,V4 C V1,V2,V5,V4,V3 D V1,V2,V3,V4,V5 正确答案:D 答案解析: 根据题意，只需根据深度遍历的策略进行遍历。对于A，先访问V1，然后访问与V1邻接且未被访问的任一顶点(满足的有V2,V3和V5)，此时访问V5，然后从V5出发，访问与V5邻接目未被访问的任一顶点(满足的只有V4)，然后从V4出发，访问与V4邻接且未被访问的任一节点(满足的只有V3)，然后从V3出发，访问与V3邻接且未被访问的任一顶点(满足的只有V2)，结束遍历。选项B和C的分析方法和A相同。选项D，先访问V1，在从V1出发，访问V1邻接目未被访问的任一顶点(满足的有V2.V3,V5)，然后从V2出发访问与V2邻接且未被访问的任一顶点(满足的只有V5)。按规则本应该访问V5，但是选项D却访问了V3D错误。

对如下无向图进行遍历，则下列选项中，不是广度优先遍历序列的是()。

A hcabdegf B eafgbhcd C dbcahefg D abcdhefg

正确答案:D 答案解析 : 根据广度遍历算法，其中D是深度优先遍历，不是广度优先遍历。

以下关于图的遍历的叙述中，正确的是()

A 图的遍历是从给定的源点出发对每一个顶点仅访问一次的过程 B 图的深度优先遍历方法不适用于无向图 C 使用队列对图进行广度优先遍历 D 图中有回路时则无法进行遍历

正确答案:C 答案解析: 使用队列对图进行广度优先遍历。

设有向图G 具有n个顶点、e条弧，采用邻接表存储，则完成广度优先遍历的时间复杂度为()

A O(n+e) B O(n^2) C O(e^2) D O(n*e) 正确答案:A

最小生成树

假设有n个节点，那么这个图的最小生成树有n-1条边(不会形成环路，是树非图)，这n-1条边应该会将所有顶点都连接成一个树，并且这些边的权值之和最小，因此称为最小生成树。共有下列两种算法

普里姆算法

从任意顶点开始，每次选择连接树中顶点与非树中顶点的最小边，将其对应的顶点加入生成树，然后从该顶点出发继续选边，直到所有顶点都被包含。普里姆算法的时间复杂度为0(n^2)，与图中的边数无关，因此该算法适合于求边稠密的网的最小生成树。

实现Prim算法利用的算法是(64)，采用Prim算法求解下图的最小生成树，该算法的设计策的权值是

A 分治法 B 动态规划法 C 贪心算法 D 递归算法

A 15 B 18 C 24 D 2

正确答案:C A 答案解析: Prim算法:从某一个顶点开始构建生成树，每次将代价最小的新顶点纳入生成树，直到所有的顶点都纳入为E.贪心法做出的选择是对于当前所处状态的最优选择，它的解决问题的视角是微观的“局部”，而不是从全局宏观的角度思考和看待问题，根据这样的性质，要求贪心法解决的问题有“无后效性”Prim算法是非常典型的贪心算法应用，几乎体现了贪心法的全部特点，prim算法的贪心策略是每次以选取距离已经生成的部分权值最小的边作为“贪心选择的标准”。本题选择C选项。根据prim算法的贪心策略是每次以选取距离已经生成的部分权值最小的边作为“贪心选择的标准”，选择边AC，DF，BE，CF，BC，即1+2+3+4+5=15，本题选择A选项。

克鲁斯卡尔算法

这个算法是从边出发的，因为本质是选取权值最小的n-1条边，因此，就将边按权值大小排序，依次选取权值最小的边，直至括所有节点，要注意，每次选边后要检查不能形成环路。克鲁斯卡尔算法的时间复杂度为0(eloge)，.因此该算法适合于求边稀疏的网的与图中的顶点数无关，最小生成树。

迪杰斯特拉(Diikstra)算法用于求解图上的单源点最短路径。该算法按路径长度递增次序产生最短路径，本质上说，该算法是一种基干()策略的算法。

A 分治 B 动态规划 C 贪心 D 回溯

正确答案:C 答案解析: 本题考查算法的设计策略。单源点最短路径问题是指给定图G和源点v0，求从v0到图G中其余各项点的最短路径，迪杰斯特拉(Diikstra算法是一个求解单源点最短路径的经典算法，其思想是:把图中所有的顶点分成两个集合S和T，S集合开始时只包含顶点v0，T集合开始时包含图中除了顶点v0之外的所有顶点。凡是以v0为源点，已经确定了最短路径的终点并入S集合中，顶点集合T则是尚末确定最短路径的顶点集合。按各顶点与v0间最短路径长度递增的次序，逐个把T集合中的顶点加入到S集合中，使得从0到S集合中各顶点的路径长度始终不大于从0到集合中各顶点的路径长度。该算法是以一种贪心的方式将T集合中的顶点加入到S集合中的，而且该贪心方法可以求得问题的最优解。

拓扑序列

若图中一个节点入度为0，则应该最先执行此活动，而后删除掉此节点和其关联的有向边，再去找图中其他没有入度的结点，执行活动，依次进行，示例如下(有点类似于进程的前趋图原理):

拓扑排序是将有向图中所有顶点排成一个线性序列的过程，并且该序列满足:若在AOV网中从顶点vi到vj有-条路径，则顶点vi必然在顶点vj之前。对于下图所示的有向图，()是其拓扑序列。

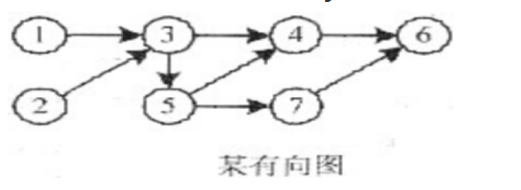
A 1234576 B 1235467 C 2135476 D 2134567 正确答案:C 答案解析: 对于图所示的有向图，其拓扑序列为2135476。选C

重点回顾

• 图由顶点和边组成，可以表示为一组顶点和一组边构成的集合。

• 相较于线性关系（链表）和分治关系（树），网络关系（图）具有更高的自由度，因而更复杂。

• 有向图的边具有方向性，连通图中的任意顶点均可达，有权图的每条边都包含权重变量。

• 邻接矩阵利用矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，用 1 或 0 表示两个顶点之间有边或无边。邻接矩阵在增删查改操作上效率很高，但空间占用较多。

• 邻接表使用多个链表来表示图，第 i 个链表对应顶点 i ，其中存储了该顶点的所有邻接顶点。邻接表相对于邻接矩阵更加节省空间，但由于需要遍历链表来查找边，因此时间效率较低。

• 当邻接表中的链表过长时，可以将其转换为红黑树或哈希表，从而提升查询效率。

• 从算法思想的角度分析，邻接矩阵体现了“以空间换时间”，邻接表体现了“以时间换空间”。

• 图可用于建模各类现实系统，如社交网络、地铁线路等。

• 树是图的一种特例，树的遍历也是图的遍历的一种特例。

• 图的广度优先遍历是一种由近及远、层层扩张的搜索方式，通常借助队列实现。

• 图的深度优先遍历是一种优先走到底、无路可走时再回溯的搜索方式，常基于递归来实现。

排序⭐

直接插入排序

插入排序（insertion sort）是一种简单的排序算法，它的工作原理与手动整理一副牌的过程非常相似。具体来说，我们在未排序区间选择一个基准元素，将该元素与其左侧已排序区间的元素逐一比较大小，并将该元素插入到正确的位置。

要注意的是，前提条件是前i-1个元素是有序的，第i个元素依次从第i-1个元素往前比较，直到找到一个比第i个元素值小的元素，而后插入，插入位置及其后的元素依次向后移动

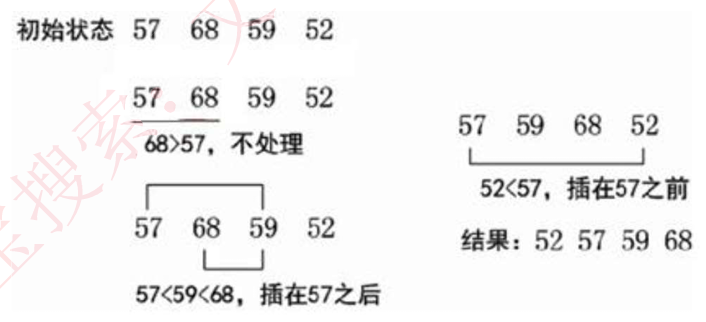
当给出一队无序的元素时，首先，应该将第1个元素看做是一个有序的队列，而后从第2个元素起，按插入排序规则，依次与前面的元素进行比较，直到找到一个小于他的值，才插入。示例如下图所示

下图中，59依次向前比较，先和68比较，再和57比较，发现57比他小，才插初始状态 57 68 59 52

对以下四个序列用直接插入排序方法由小到大进行排序时，元素比较次数最少的是()。

A 89，27，35，78，41，15 B 27,35，41，16，89，70 C 15，27，46，40，64，85 D 90，80，45，38，30，25

正确答案：C，当序列基本有序时，直接插入排序过程中元素比较的次数较少，当序列为逆序时，元素的比较次数最多。这里选项C中的元素按照从小到大基本有序排列，用直接插入法比较次数最少。

下列算法中，()算法可能出现下列情况:在最后一趟开始之前，所有元素都不在最终位置上。

A 堆排序 B 冒泡排序 C 直接插入排序 D 快速排序

正确答案:C 在直接插入排序中，若待排序中的最后一个元素插入表的第一个位置，则前面的有序子序列中的所有元素都不在最终位置上

将数组{1，1，2，4，7，5}从小到大排序，若采用()排序算法，则元素之间需要进行的比较次数最少，共需要进行()次元素之间的比较。

A 直接插入 B 归并 C 堆 D 快速 A 5 B 6 C 7 D 8

正确答案:A B答案解析: 直接插入排序算法是:每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序。第1趟比较前两个数，然后把第2个数按大小插入到有序表中:第2趟把第3个数据与前两个数从前向后扫描，把第3个数按大小插入到有序表中:依次进行下去，进行了(n-1)趟扫描以后就完成了整个排序过程。直接插入排序属于稳定的排序，最坏时间复杂性为(n2)，空间复杂度为0(1)。依题意，将数组(1，1，2，4，7，5}从小到大排序，若采用直接插入排序算法，则元素之间需要进行的比较次数最少，共需要进行6次元素之间的比较。

对n个基本有序的整数进行排序，若采用插入排序算法，则时间和空间复杂度分别为( 62);若采用快速排席算法，则时间和空间复杂度分别为(63)。

0(n^2)和O(n) 0(n)和O(n) 0(n^2)和0(1) 0(n) 和0(1)

正确答案:D 答案解析:若数据基本有序,对插入排序算法而言，则可以在近似线性时间内完成排序，即O(n);而对于快速排序而言，则是其最坏情况，即O(n^2)。两个算法在排序时仅需要一个额外的存储空间，即空间复杂度为常数O(1)。(这里比较特殊，基本有序的情况下，快速排序因为不需要做交换处理，所以不需要存储额外数据，每一轮记录一次基准数值，空间复杂度只需要O(1)，本题选择D选项。

0(n^2)和O(n) 0(nlgn)和O(n) 0(n^2)和0(1) 0(nlgn)和O(1)

正确答案:C 答案解析:若数据基本有序,对插入排序算法而言，则可以在近似线性时间内完成排序，即O(n);而对于快速排序而言，则是其最坏情况，即O(n^2)。两个算法在排序时仅需要一个额外的存储空间，即空间复杂度为常数O(1)。(这里比较特殊，基本有序的情况下，快速排序因为不需要做交换处理，所以不需要存储额外数据，每一轮记录一次基准数值，空间复杂度只需要O(1))，本题选择C选项。

希尔排序

希尔排序（Shell Sort）是一种改进版的插入排序，也叫缩小增量排序。它通过比较距离较远的元素来减少元素移动的次数，从而提高效率，特别适合中等规模数据排序。

1. 选择一个初始的“间隔”gap（通常是数组长度的一半），将数组分成若干组；

2. 对每一组进行插入排序；

3. 缩小gap（通常是 gap /= 2），重复步骤 2；

4. 当gap为1时，再进行一次直接插入排序，排序完成。

---

📦 举个例子：对数组 [8, 9, 1, 7, 2, 3, 5, 4, 6, 0] 进行希尔排序

初始数组： [8, 9, 1, 7, 2, 3, 5, 4, 6, 0]

第一步：gap = 5，分成5组，进行插入排序（索引相差5的为一组）

组1: [8, 3] → 排序后: [3, 8]
组2: [9, 5] → 排序后: [5, 9]
组3: [1, 4] → 排序后: [1, 4]
组4: [7, 6] → 排序后: [6, 7]
组5: [2, 0] → 排序后: [0, 2]

替换回原数组：

[3, 5, 1, 6, 0, 8, 9, 4, 7, 2]

第二步：gap = 2，分组并排序后（两两插入排序）：

[1, 3, 0, 5, 2, 6, 4, 8, 7, 9]

第三步：gap = 1（普通插入排序）最终排序结果：

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

简单选择排序

选择排序（selection sort）的工作原理非常简单：开启一个循环，每轮从未排序区间选择最小的元素，将其放到已排序区间的末尾。

采用简单选择排序算法对序列(49，38，65，97，76，13，27，49)进行非降序排序，两趟后的序列为

A (13，27，65，97，76，49，38，49) B (38，49，65，76，13，27，49，97) C (13，38，65，97，76，49，27，49) D (38，49，65，13，27，49，76，97)

正确答案:A答案解析: 简单选择排序第一趟是从左到右检索

堆排序⭐

关键字序列{K，K，…，K)，当且仅当满足下列关系时称其为堆，其中2i和 2i+1 需不大于 n。

堆排序的基本思想是:对一组待排序记录的关键字，首先按堆的定义排成一个序列(即建立初始堆)，从而可以输出堆顶的最大关键字(对于大根堆而言)，然后将剩余的关键字再调整成新堆，便得到次大的关键字，如此反复，直到全部关键字排成有序序列为止。

初始堆的建立方法是:将待排序的关键字分放到一棵完全二叉树的各个结点中(此时完全二叉树并不一定具备堆的特性)，显然，所有i>”的结点K都没有子结点，以这样的飞为根的子树已经是堆，因此初始建堆可从完全二叉树的第ii=“)个结点 K开始，通过调整,还步使以K、…、K,、K为根的子树满足堆的定义。

为序列(55,60,40,10,80,65,15,5,75)建立初始大根堆的过程如图所示

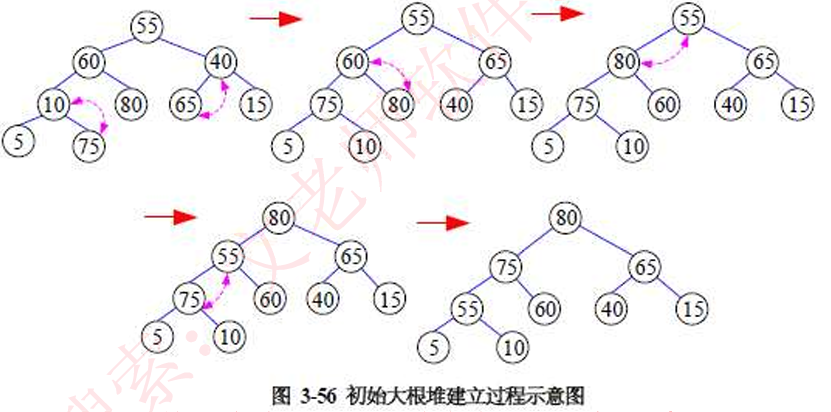
由上图可知，首先将给出的数组按完全二叉树规则建立，而后，找到此完全二叉树的最后一个非叶子节点(也即最后一颗子树)，比较此非叶子节点和其两个孩子结点的大小，若小，则与其孩子结点中最大的结点进行交换;依据此规则再去找倒数第二个非叶子节点;这是只有一层的情况，当涉及到多层次时又打破了之前的堆，因此，又要进行变换。

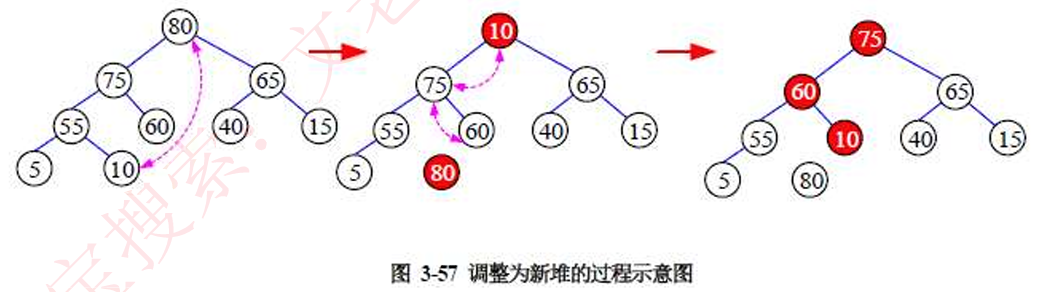
建立初始堆后，开始排序，每次取走堆顶元素(必然是最大的)，而后将堆中最后一个元素移入堆顶，而后按照初始建堆中的方法与其孩子结点比较大小依次向下判断交换成为一个新的堆，再取走堆顶元素，重复此过程。堆排序适用于在多个元素中找出前几名的方案设计，因为堆排序是选择排序而且选择出前几名的效率很高。

堆排序是一种 (选择)排序，m个元素进行堆排序时，其时间复杂性为 ()。请回答第2个问题

O(m) O(m2) O(log2m) O(mlog2m)

正确答案：D，堆排序是利用堆这一特殊的树形结构进行的选择排序，它有效地改进了直接选择排序，提高了算法的效率,堆排序的整个过程是:构造初始堆，将堆的根节点和最后一个节点交换，重新调整成堆，再交换，再调整直到完成排序。其时间复杂度是O(nlog2n)。

对于n个关键字进行堆排序，最坏情况下的时间复杂度为()。

O (log2n) O(n) O (nlog2n) O (n2)

正确答案：C，答案解析: 任何情况下堆排序的时间复杂度O(nlog2n)

堆排序是一种 ()排序，m个元素进行堆排序时，其时间复杂性为()。

归并 交换 选择 插入

正确答案:C 答案解析:堆排序是利用堆这一特殊的树形结构进行的选择排序，它有效地改进了直接选择排序，提高了算法的效率堆排序的整个过程是:构造初始堆，将堆的根节点和最后一个节点交换，重新调整成堆，再交换，再调整直到完成排序。其时间复杂度是O(nlog2n)。

有一组数据15,9,7,8,20，-1,7,4，用堆排序的筛选方法建立的初始小根堆为(C)

-1489 20715,7 -1,715,748209 -1,478201579 以上均不对

优先队列通常采用”堆“数据结构实现，向优先队列中插入一个元素的时间复杂度为() Θ(n) Θ(1) Θ(lgn) Θ(n^2) 正确答案:C 本题考查数据结构基础知识。普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删答案解析:除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出(largest-in，first-out)的行为特征。优先队列一般采用二叉堆数据结构实现，由于是二叉堆，所以插入和删除一个元素的时间复杂度均为O(lgn)。

冒泡排序

冒泡排序通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样，因此得名冒泡排序。冒泡过程可以利用元素交换操作来模拟：从数组最左端开始向右遍历，依次比较相邻元素大小，如果“左元素 > 右元素”就交换二者。遍历完成后，最大的元素会被移动到数组的最右端。

在第一趟排序之后，一定能把数据表中最大或最小元素放在其最终位置上的排序算法是()。

A 冒泡排序 B 直接插入排序 C 快速排序 D 归并排序

正确答案:A,答案解析:第i趟冒泡排序是从第1个元素到第n-i+1个元素依次比较相邻两个元素的关键字，并在“逆序”时交换相邻元素，其结果是这n-i+1个元素中最大的元素被交换到第n-i+1的位置上。那么第一趟排序之后，就一定能把数据表中最大的元素放在其最终有序位置上。而其他排序算法均不能实现此要求。举例说明:要排序数组:int[l arr={6,3,8,2.9,1};

第一趟排序:第一次排序:6和3比较，6大于3交换位置:368291 第二次排序:6和8比较，6小于8不交换位置:368291 第三次排序:8和2比较，8大于2交换位置:362891 第四次排序:8和9比较，8小于9不交换位置:362891 第五次排序:9和1比较:9大于1362819交换位置:第一趟总共进行了5次比较， 排序结果:362819 可以看出第一趟排序之后，9被排列在最终位置。

对于一个初始无序的关键字序列，在下面的排序方法中，()第一趟排序结束后，一定能将序列中的某个元素在最终有序序列中的位置确定下来 ①直接插入排序②冒泡排序③简单选择排序4堆排序快速排序 ⑥归并排序

①②③⑥ ①②③⑤⑥ ②③④⑤ ③④⑤ ⑥

正确答案：C，答案解析: 每次排序能够确定至少一个元素最终位置的排序

快速排序:每次可以确定指定的哨兵元素位置。 冒泡排序:每次可以确定最大元素位置。 堆排序:每一次排序时，都是将堆顶的元素和最后一个节点互换，然后调整堆，再将堆大小减1。所以每-次排序堆顶元素确定。简单选择排序:每次将最大的数放到最后。每次确定最大元素的位置。

对一组数据2,12,16,88,5,10进行排序，如果前3趟排序结果如下:第一趟排序结果:2,12,16,5,10,88第二趟排序结果:2,12,5,10,16,88第三趟排序结果:2.5,10,12,16,88 则采用的排序算法可能是() 冒泡排序 希尔排序 归并排序 基数排序 正确答案:A 分别用其他3中排序算法执行数据，归并排序的第一趟排序后的结果是2,12,16,88,5,10。基数排序第一趟后答案解析:2的结果是10,2,12,5,16,88。希尔排序显然不符合，只有冒泡排序符合。

快速排序⭐

快速排序（quick sort）是一种基于分治策略的排序算法，运行高效，应用广泛。快速排序的核心操作是“哨兵划分”，其目标是：选择数组中的某个元素作为“基准数”，将所有小于基准数的元素移到其左侧，而大于基准数的元素移到其右侧

1. 选取数组最左端元素作为基准数，初始化两个指针 i 和 j 分别指向数组的两端。

2. 在循环中每轮中使用 i（j）分别寻找第一个比基准数大（小）的元素，然后交换这两个元素。

3. 循环执行步骤 2 ，直到 i 和 j 相遇时停止，最后将基准数交换至两个子数组的分界线。

要注意的是：每次都是和基准值进行比较，因此最终是以基准值为中间，将队列分成两块。只有当和基准值发生了交换，才变换high和low指针的计数，否则会一直low--下去。

上图中，最终以57为界，左边都是小于57的元素，右边都是大于57的元素，完成一次快速排序，接着对两块再分别进行递归即可。

对数组A=(2,8,7,1.3,5,6,4)用快速排序算法的划分方法进行一趟划分后得到的数组A 为())(非递减排序，以最后一个元素为基准元素)。进行一趟划分的计算时间为()。

A (1,2.873,5,64) B (1,2,3,4,.87.5,6) C (2 3,1.47,5.6,8) D (2,1,3,4.8,7,5,6)

A O(1) B O(lgn) C O(n) D O(nlgn)

正确答案：C，C，快速排序的思想是从待排序列中取一个元素作为中心，所有比他小或相等的元素一律放在前面，所有比他的的元素一律放在后面，形成左右两个表，然后再对各个子表 重新选择中心元素，并按此规则调整，直到每个子表的元素只剩下一个，此时便成为有序 序列了。在这里设置两个指针ì和j，分别从左往右找比基准元素大的和从右往左找比基准 元素小的元素。本题中告诉了基准元素是最后一个元素 4，第一次用2和4进行比较，因为2比4小，所以位置不变，指针移动到第二个元素 8，因为8比4大，所以，他们进行交换。2.4.7.1.3.5.6.8 此时，从指针所指向的元素 6开始比较，因为6比4大，所以位置不动,i指针从右往左 前移，5 和4 进行比较，5 还是比 4大，位置不变化，继续前移i指针，3 和4进行比较，因为3比4小，所以,3 和4位置互换,2.3.7.1.4.5.6.8 此时，移动ì指针，用7和4进行比 较，因为7比4大，所以他们互换位置，此时序列变为 2.3.4.1.7.5.6.8，再移动j指针，1和4进行比较，因为1比4小，所以互换位置，序列变为2.3.1.4.7.5.6.8。因此，经过第一趟排 序后序列为 C。

通过设置基准(枢轴)元素将待排序的序列划分为两个子序列，使得其一个子序列的元素均不大于基准元素，另-个子序列的元素均不小于基准元素，然后再分别对两个子序列继续递归地进行相同思路的排序处理，这种排序方法称为(A)。

快速排序 冒泡排序 归并排序 简单选择排序

为实现快速排序算法，待排序列适合采用()。

顺序存储 链式存储 散列存储 索引存储

正确答案:A 答案解析: 这道题当成一个常识题。大多数内部排序算法都只适用于顺序存储。

归并排序⭐

归并排序（merge sort）是一种基于分治策略的排序算法，包含“划分”和“合并”阶段。

1. 划分阶段：通过递归不断将数组从中点处分开，将长数组的排序问题转换为短数组的排序问题。

2. 合并阶段：当子数组长度为 1 时终止划分，开始合并，持续地将左右两个较短的有序数组合并为一个较长的有序数组，直至结束。

要仔细理解上述过程，一般归并排序都是用来合并多个线性表的，对单列数据，二路归并排序可以对元素进行两两合并，示例如下：

对第三次归并，将52与28比较，28小，放入新表头，52再与33比较，33放入新表，52再与72比较，52放入新表，57再与72比较，57放入新表.

在最好和最坏情况下的时间复杂度均为0(nlogn)且稳定的排序方法是(52)。

A 冒泡排序 B 快速排序 C 堆排序 D 归并排序

正确答案:D，答案解析： 基数排序最坏的时间复杂度均为O(d(n+rd));快速排序最好和最坏情况下的时间复杂度分别为O(n2)和O(nlogn)且不稳定;堆排序在最好和最坏情况下的时间复杂度均为0(nlogn)但不稳定;归并排序是在最好和最坏情况下的时间复杂度均为O(nlogn)且稳定的排序方法。

若排序前后关键字相同的两个元素相对位置不变，则称该排序方法是稳定的。()排序是稳定的。

A 归并 B 快速 C 希尔 D 堆 正确答案：A 答案解析: 在快速排序、希尔排序和堆排序中，元素的移动不保证在相邻位置间进行，因此不能确保关键字相同的两个元素在排序前后的相对位置不变。在归并排序中，对于关键字相同的两个元素，排在前面的元素可确保先进入最终的有序序列，因此归并排序是稳定的。

归并排序算法在排序过程中，将待排序数组分为两个大小相同的子数组，分别对两个子数组采用归并排序算法进行排序，排好序的两个子数组采用时间复杂度为0(n)的过程合并为一个大数组。根据上述描述，归并排序算法采用了()算法设计策略。归并排序算法的最好和最坏情况下的时间复杂度为()。

分治 动态规划 贪心 回溯

O(n)和O(nlgn) O(n)和O(n^2) O(nlgn) 和O(nlgn) O(nlgn) 和O(n^2)

答案：AC 归并排序将问题先分解、再处理、再合并的方式采用了分治法的思想。

下列排序算法中，占用辅助存储空间最多的是 （）。 归并排序 快速排序 堆排序 冒泡排序

正确答案:A 答案解析: 两路归并排序的核心操作是将一维数组中前后相邻的两个有序序列归并为一个新的有序序列，空间复杂度为O(n)。是几种排序中占用辅助存储空间最多的。快速排序空间复杂度为O(logn)，堆排序和冒泡排序的空间复杂度为O(1)。

基数排序

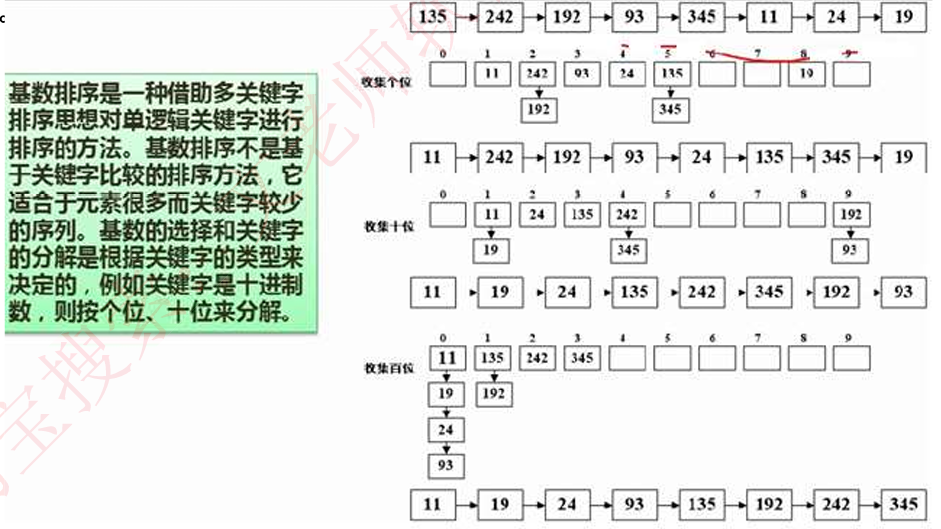
基数排序是基于多个关键字来进行多轮排序的，本质也是将问题细分，如图例子，分别按个位、十位、百位的大小作为关键字进行了三轮排序，最终得出结果

计数排序

计数排序（counting sort）通过统计元素数量来实现排序，通常应用于整数数组。

桶排序

前述几种排序算法都属于“基于比较的排序算法”，它们通过比较元素间的大小来实现排序。此类排序算法的时间复杂度无法超越 𝑂(𝑛log⁡𝑛) 。接下来，我们将探讨几种“非比较排序算法”，它们的时间复杂度可以达到线性阶。桶排序（bucket sort）是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶，每个桶对应一个数据范围，将数据平均分配到各个桶中；然后，在每个桶内部分别执行排序；最终按照桶的顺序将所有数据合并。

排序算法总结

• 冒泡排序通过交换相邻元素来实现排序。通过添加一个标志位来实现提前返回，我们可以将冒泡排序的最佳时间复杂度优化到 𝑂(𝑛) 。

• 插入排序每轮将未排序区间内的元素插入到已排序区间的正确位置，从而完成排序。虽然插入排序的时间复杂度为 𝑂(𝑛2) ，但由于单元操作相对较少，在小数据量的排序任务中非常受欢迎。

• 快速排序基于哨兵划分操作实现排序。在哨兵划分中，有可能每次都选取到最差的基准数，导致时间复杂度劣化至 𝑂(𝑛2) 。引入中位数基准数或随机基准数可以降低这种劣化的概率。尾递归方法可以有效地减少递归深度，将空间复杂度优化到 𝑂(log⁡𝑛) 。

• 归并排序包括划分和合并两个阶段，典型地体现了分治策略。在归并排序中，排序数组需要创建辅助数组，空间复杂度为 𝑂(𝑛) ；然而排序链表的空间复杂度可以优化至 𝑂(1) 。

• 桶排序包含三个步骤：数据分桶、桶内排序和合并结果。它同样体现了分治策略，适用于数据体量很大的情况。桶排序的关键在于对数据进行平均分配。

• 计数排序是桶排序的一个特例，它通过统计数据出现的次数来实现排序。计数排序适用于数据量大但数据范围有限的情况，并且要求数据能够转换为正整数。

• 基数排序通过逐位排序来实现数据排序，要求数据能够表示为固定位数的数字。

• 总的来说，我们希望找到一种排序算法，具有高效率、稳定、原地以及正向自适应性等优点。然而，正如其他数据结构和算法一样，没有一种排序算法能够同时满足所有这些条件。在实际应用中，我们需要根据数据的特性来选择合适的排序算法。

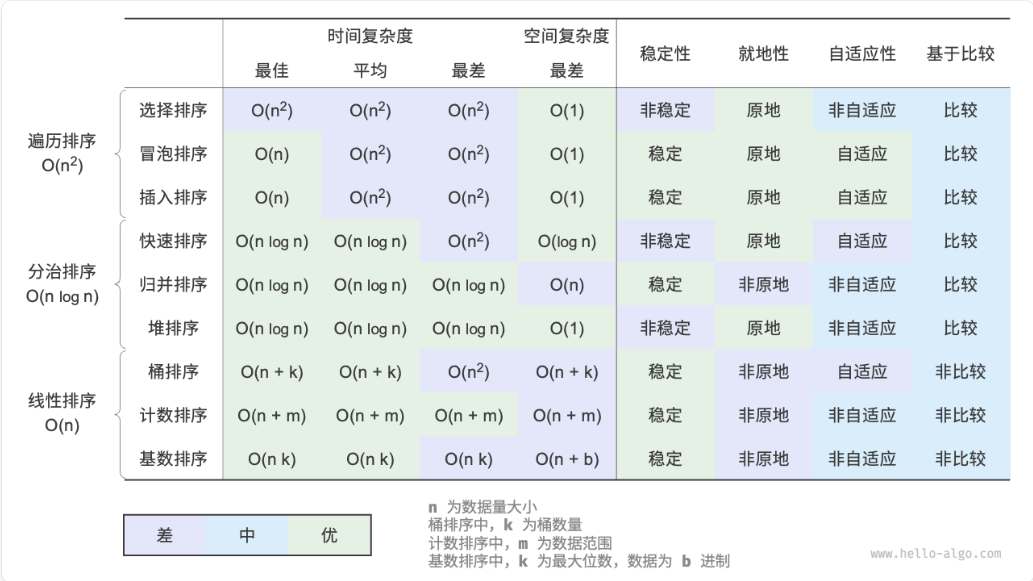
• 图 11-19 对比了主流排序算法的效率、稳定性、就地性和自适应性等。

算法分析与设计⭐

算法分析

算法特性

1. 有穷性：算法必须在有限的步骤内结束，且每一步的执行时间也必须是有限的。

2. 确定性：算法中的每一条指令必须有确切的含义，理解时不会产生二义性并且在任何条件下，算法只有唯一的一条执行路径，即对于相同的输入只能得出相同的输出。

3. 可行性：算法的每一步操作必须是可实现的，且能在有限时间内完成。

4. 输入：一个算法有零个或多个输入，这些输入取自于某个特定的对象的集合

5. 输出：一个算法有一个或多个输出，这些输出是同输入有着某些特定关系的

有穷性和可行性区分：

特性	关注点	违反情况举例
有穷性	算法能否终止（步骤有限）	无限循环、未定义终止条件
可行性	每一步是否可执行且资源合理	操作不明确、资源需求超出实际能力（如指数时间）

复杂度分析⭐

时间复杂度是衡量算法运行时间随输入规模增长变化趋势的量，它用大O符号（O）来表示，比如：

时间复杂度	说明
O(1)	常数时间，最快
O(log n)	对数时间，如二分查找
O(n)	线性时间，如遍历数组
O(n log n)	归并排序、快速排序等
O(n²)	双层循环，如冒泡排序
O(2ⁿ)	指数时间，较慢

递归

递归是指子程序(或函数)直接调用自己或通过一系列调用语句间接调用自己

递归有两个基本要素：边界条件即确定递归到何时终止，也称为递归出口;递归模式，即大问题是如何分解为小问题的，也称为递归体

$$
n! = \begin{cases} 1 & \text{ } n = 0 \\ n \cdot (n-1)! & \text{ } n > 0 \end{cases}
$$

阶乘函数可递归地定义为：阶乘函数的自变量n 的定义域是非负整数。递归式的第一式给出了这个函数的一个初始值，是递归的边界条件。递归式的第二式是用较小自变量的函数值来表示较大自变量的函数值的方式来定义n的阶乘，是递归体。n!可以递归地计算如下:

int Factorial(int num){
	if(num==0) {
        return 1;
    }
	if(num>0) {
        return num* Factorial(num -1);
    }
}

递归算法的时间复杂度分析方法:将递归式中等式右边的项根据递归式进行替换，称为展开。展开后的项被再次展开，如此下去，直到得到一个求和表达式，得到结果。

下面书上例子有误，应该是T(n)=T(n-1)+n

每次分别将n，n-1，n-2，n-3这样往里面带入，即可得到展开式

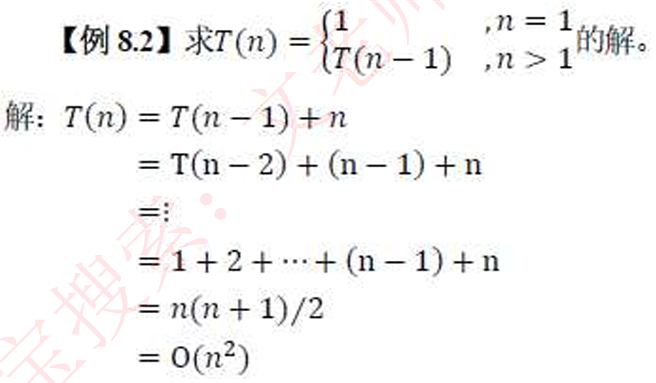
分治法⭐

分治法的设计思想是将一个难以直接解决的大问题分解成一些规模较小的相同问题，以便各个击破，分而治之。如果规模为n的问题可分解成k个子问题，1<k≤n，这些子问题互相独立且与原问题相同。分治法产生的子问题往往是原问题的较小模式，这就为递归技术提供了方便。

折半查找在有序数组A中查找特定的记录K:通过比较K和数组中的中间元素 A[mid]进行，如果相等，则算法结束;如果K小于A[mid]，则对数组的前半部分进行折半查找:否则对数组的后半部分进行折半查找。根据上述描述，折半查找算法采用了 0)算法设计策略。对有序数组(3,14,27,39,42,55,70,85,93,98)，成功査找和失败査所需要的平均比较次数分别是()(假设查找每个元素的概率是相同的)。

A 分治 B 动态规划 C 贪心 D 回溯

A 29/10和29/11 B 30/10和30/11 C 29/10 和39/11 D 30/10和40/11

正确答案:A C 答案解析:折半查找算法是一种分治法。 把数组构造成一棵二叉查找树如下图。

每次取中位数作为当前节点：构建步骤如下（递归）：

1. 取中间元素作为根节点 👉 中间是 42（第 5 位，0-based index 是 4）

2. 左边 [3, 14, 27, 39] 👉 中位数是 14，成为左子节点 → [3, 27, 39] 继续构建

3. 右边 [55, 70, 85, 93, 98] 👉 中位数是 85，成为右子节点 → [55, 70] 和 [93, 98] 继续构建

成功查找的平均比较次数计算:找到42需要1次:找到14、85需要2次:找到3、27、55、93需要3次:找到39、70、98需要4次。所以点数为1+2*2+4*3+3*4=29，平均次数为29/10.失败查找则相当于最后落到空的子树上，这棵10个结点的二又树一共有11个空的子树。到达这11棵空子树走过的路径长度总数为5*3+6*4=39，平均次数为39/11

分治算法设计技术()。

A 一般由三个步骤组成:问题划分、递归求解、合并解 B 一定是用递归技术来实现

C 将问题划分为多个规模相等的子问题 D 划分代价很小而合并代价很大

正确答案:A 答案解析:本题考查算法设计技术。分治方法是一种重要的算法设计技术(设计策略)，该策略将原问题划分成n个规模较小而结构与原问题相似的子问题:递归地解决这些子问题:然后再合并其结果，最终得到原问题的解。分治算法往往用递归技术来实现，但并非必须。分治算法最理想的情况是划分为k个规模相等的子问题，但很多时候往往不能均匀地划分子问题。分治算法的代价在划分子问题和合并子问题的解上，根据不同的问题，划分的代价和合并的代价有所不同。例如归并排序中，主要的计算代价在合并解上，而在快速排序中，主要的计算代价在划分子问题

在有n个无序无重复元素值的数组中查找第i小的数的算法描述如下:任意取一个元素r，用划分操作确定其在数组中的位置,假设元素r为第k小的数。若i等于k，则返回该元素值;若i小于k，则在划分的前半部分递归进行划分操作找第i小的数;否则在划分的后半部分递归进行划分操作找第k-i小的数。该算法是一种基于()策略的算法。 A 分治 B 动态规划 C 贪心 D 回溯 正确答案:A 答案解析: 本题考查算法的设计策略。 从题干可以看出，划分操作与快速排序中的划分操作是一样的，确定某个元素如r的最终位置，划分后，在r之前的元素都小于r，在r之后的元素都大于r(假设无重复元素)。因此可以据此确定r是数组中第几小的数。题干所述的算法把找第i小的数转换为确定任意一个元素是第几小的数，然后根据这个结果再在依据该元素划分后得到的结果在前一部分还是后一部分来继续确定某个元素为第几小的数，重复这种处理，直到找到第i小的数。这是分治策略的一个典型应用。

动态规划法⭐

特性	动态规划（DP）	分治法（D&C）
子问题是否重叠	有重叠子问题，通常会重复计算	无重叠子问题，每个子问题只计算一次
子问题的依赖性	子问题之间存在依赖（通常是后一个依赖前一个）	子问题之间相互独立，可以并行求解
解决方式	使用记忆化搜索（递归 + 缓存） 或 递推	使用递归解决各个子问题，最终合并结果
是否需要缓存	是，必须保存子问题结果以避免重复计算	否，不需要缓存，直接合并子问题结果即可
示例算法/问题	背包问题、斐波那契数列、最长公共子序列等	归并排序、快速排序、二分查找、汉诺塔等

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合用动态规划法求解的问题，经分解得到的子问题往往不是独立的。若用分治法来解这类问题，则相同的子问题会被求解多次，以至于最后解决原问题需要耗费指数级时间。

然而，不同子问题的数目常常只有多项式量级。如果能够保存已解决的子问题的答案，在需要时再找出已求得的答案，这样就可以避免大量的重复计算，从而得到多项式时间的算法。为了达到这个目的，可以用一个表来记录所有已解决的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解，每个解都对应于一个值，我们希望找到具有最优值(最大值或最小值)的那个解。当然，最优解可能会有多个，动态规划算法能找出其中的一个最优解。设计一个动态规划算法，通常按照以下几个步骤进行。

1. 找出最优解的性质，并刻画其结构特征。

2. 递归地定义最优解的值。

3. 以自底向上的方式计算出最优值。

4. 根据计算最优值时得到的信息，构造一个最优解。

步骤(1)~(3)是动态规划算法的基本步骤。在只需要求出最优值的情形下，步骤(4)可以省略。若需要求出问题的一个最优解，则必须执行步骤(4)

对于一个给定的问题，若其具有以下两个性质，可以考虑用动态规划法来求解。

1. 最优子结构。如果一个问题的最优解中包含了其子问题的最优，也就是说该问题具有最优子结构。当一个问题具有最优子结构时，提示我们动态规划法可能会适用，但是此时贪心策略可能也是适用的。

2. 重叠子问题。重叠子问题指用来解原问题的递归算法可反复地解同样的子问题，而不是总在产生新的子问题。即当一个递归算法不断地调用同一个问题时，就说该问题包含重叠子问题。

典型应用:0-1：背包问题

有n 个物品，第i个物品价值为vi，重量为wi，其中vi和wi均为非负数，背包的容量为W，W为非负数。现需要考虑如何选择装入背包的物品，使装入背包的物品总价值最大。

满足约束条件的任一集合(x1，x2，…，xn)是问题的一个可行解，问题的目标是要求问题的一个最优解。考虑一个实例，假设n=5，W=17，每个物品的价值和重量如表所示，可将物品1、2和5 装入背包，背包未满，获得价值22，此时问题解为(1，1，0，0，1);也可以将物品4和5装入背包，背包装满，获得价值24，此时解为(0，0，0，1，1)。

(1)刻画0-1背包问题的最优解的结构。可以将背包问题的求解过程看作是进行一系列的决策过程，即决定哪些物品应该放入背包，哪些物品不放入背包。如果一个问题的最优解包含了物品n，即xn=1，那么其余x1，x2，…，xn-1一定构成子问题1,2,…, n-1 在容量为W-wn时的最优解。如果这个最优解不包含物品n，即xn=0，那么其余x1，x2，…，xn-1-定构成子问题1,2,…, n-1 在容量为W 时的最优解,

(2)递归定义最优解的值根据上述分析的最优解的结构递归地定义问题最优解。设ci,w表示背包容量为w时i个物品导致的最优解的总价值，得到下式。显然，问题要求c[n,W]。

在求解某问题时，经过分析发现该问题具有最优子结构性质，求解过程中子问题被重复求解，则采用()算法设计策略，以深度优先的方法是搜索解空间，则采用()算法设计策略。

A 分治 B 动态规划 C 贪心 D 回溯

A 动态规划 B 贪心 C 回溯 D 分治

正确答案:B C 答案解析:动态规划算法总体思想:如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法从根开始计算，到找到位于某个节点的解，回溯法(深度优先搜索)作为最基本的搜索算法，其采用了一种“一直向下走，走不通就掉头”的思想(体会“回溯”二字)，相当于采用了先根遍历的方法来构造搜索树。

在求解某问题时，经过分析发现该问题具有最优子结构和重叠子问题性，宜采用()算法设计策略得到最优解;若定义问题的解空间，并以广度优先的探索问题的解空间，则采用的是()算法设计策略。

A 分治 B 贪心 C 动态规划 D 回溯

A 动态规划 B 贪心 C 回溯 D分支限界

正确答案:C D适合应用动态规划方法求解的最优化问题应该具备两个要素:最优子结构和子问题重叠动态规划算法:动态规划过程是:每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

贪心算法:所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择。必须注意的是，贪心算法不是对所有问题都能得到整体最优解，选择的贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。

回溯算法：回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

分支限界算法：所谓“分支”就是采用广度优先的策略，依次搜索E-结点的所有分支，也就是所有相邻结点，抛弃不满足约束条件的结点，其余结点加入活结点表。然后从表中选择一个结点作为下一个E-结点，继续搜索。

贪心法⭐

和动态规划法一样，贪心法也经常用于解决最优化问题。与动态规划法不同的是，贪心法在解决问题的策略上是仅根据当前已有的信息做出选择，而且一旦做出了选择，不管将来有什么结果，这个选择都不会改变。换而言之，贪心法并不是从整体最优考虑，它所做出的选择只是在某种意义上的局部最优。这种局部最优选择并不能保证总能获得全局最优解，但通常能得到较好的近似最优解。

贪心法问题一般具有两个重要的性质。

1. 最优子结构。当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构。问题具有最优子结构是该问题可以采用动态规划法或者贪心法求解的关键性质。

2. 贪心选择性质。指问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来得到。这是贪心法和动态规划法的主要区别。证明一个问题具有贪心选择性质也是贪心法的一个难点。

贪心法典型应用：背包问题

背包问题的定义与0-1背包问题类似，但是每个物品可以部分装入背包，即在0-1背包问题中，xi=0或者xi=1;而在背包问题中，0≤xis1。为了更好地分析该问题，考虑一个例子:n=5，W=100，下表给出了各个物品的重量、价值和单位重量的价值。假设物品已经按其单位重量的价值从大到小排好序

为了得到最优解，必须把背包放满。现在用贪心策略求解，首先要选出一杯拿铁热量。

1. 按最大价值先放背包的原则。

2. 按最小重量先放背包的原则。

3. 按最大单位重量价值先放背包的原则:

利用贪心法求解0/1背包问题时，(能够确保获得最优解。用动态规划方法求解 0/1背包问题时，将“用前i个物品来装容量是X的背包”的0/1背包问题记为KNAP(1,i,X)，设fi(x)是KNAP(1,i,X)最优解的效益值，第;个物品的重量和放入背包后取得效益值分别为 wj和pj(j=1~n)。则依次求解f0(x)、f1(x)、…、fn(X)的过程中使用的递推关系式为 ()。

A 优先选重量最小物品 B 优先选效益最大的物品 C 优先选取单位重量效益最大的物品 D 没有任何准则

A fi(x)=min{fi-1(x),fi-1(x)+pi} B fi(x)=max{fi-1(x),fi-1 (X-Wi)+pi}

C fi(x)=min{fi-1(x-wi),fi-1(X-wi)+pi} D fi(x)=max{fi-1(X-wi),fi-1(X)+pi}

正确答案:C B 利用贪心法可以解决普通背包问题(即允许将物品的一部分装入背包)，此时使用“优先选取单位重量效益最大的物品”的量度标准可以获得问题最优解，但是贪心法不能用来求解0/1背包问题，题目中供选择的A、B、C三种量度标准均不能确保获得最优解。

用动态规划求解0/1背包问题时，按照题目中约定的记号。KNAP(1i,X)的最优解来自且仅来自于以下两种情况之一:(1)第i个物品不装入背包，此时最优解的值就是子问题KNAP(1,i-1,Ⅺ的最优解的效益值，即为fi-1(X;(2)第i个物品装入背包，最优解的值为第ì个物品的效益值与子问题 KNAP(1,i-1,X-wi)的最优解效益值之和，即为fi-1(X-wi)+pi。综上，KNAP(1,i,X)最优解的值为以上两种情况中效益值更大者，即取max

某货车运输公司有一个中央仓库和n个运输目的地，每天要从中央仓库将货物运输到所有运输目的地，到达每个运输目的地一次6且仅一次，最后回到中央仓库。在两个地点和之间运输货物存在费用Ci。为求解旅行费用总和最小的运输路径，设计如下算法:首先选择离中央仓库最近的运输目的地1，然后选择离运输目的地1最近的运输目的地2，…每次在来访问过的运输目的地中选择离当前运输目的地最近的运输目的地，最后回到中央仓库。该算法采用了()算法设计策略，其时间复杂度为()。

A 分治 B 动态规划 C 贪心 D 回溯

A O(㎡) B O(n) C O (nlgn) D O(1)

正确答案:C A 由于每次选择下一个要访问的城市时都是基于与当前最近的城市来进行，是一种贪心的选择策略，因此该算法采用的是贪心算法设计策略。而货车从中央仓库出发，第1个要到达的目的地是在n个日的地中选择一个第2个要到达的目的地是在n-1个日的地中选择一个，…，第n个要到达的目的地是在1个目的地中选择个，所以该算法的时间复杂度为n+(n-1)+..+1=n*(n-1)/2=O(㎡)

考虑下述背包问题的实例。有5件物品，背包容量为100，每件物品的价值和重量如下所示，并已经按照物品的单位重量价值从大到小排好序。根据物品单位重量价值大优先的策略装入背包中，则采用了()设计策略。考虑0/1背包问题(每件物品或者全部装入背包或者不装入背包)和部分背包问题(物品可以部分装入背包)，求解该实例得到的最大价值分别为()。

A 分治 B 贪心 C 动态规划 D 回溯

A 605和630 B 605和605 C 430和630 D 630和430

正确答案:B C 答案解析: 贪心算法(又称贪婪算法)是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。采用0/1背包考虑该问题时，只能放入1、2、3号物品，故总价值为430，采用部分背包可以将物品拆分故放入1、2、3号物品后还可以将编号4的物品部分的装入，使得背包容量尽量的满，故总容量为630。

在一条笔直公路的一边有许多房子，现要安装消防栓，每个消防栓的覆盖范围远大于房子的面积，如下图所示。现求解能覆盖所有房子的最少消防栓数和安装方案(问题求解过程中，可将房子和消防栓均视为直线上的点)。

该问题求解算法的基本思路为:从左端的第一栋房子开始，在其右侧m米处安装一个消防栓，去掉被该消防栓覆盖的所有房子。在剩余的房子中重复上述操作，直到所有房子被覆盖。算法采用的设计策略为();对应的时间复杂度为()。假设公路起点A的坐标为0，消防栓的覆盖范围(半径)为20米，10栋房子的坐标为(10,20,30,35,60,80,160,210,260,300)，单位为米。根据上述算法，共需要安装 ()个消防栓。以下关于该求解算法的叙述中，正确的是()

A 分治 B 动态规划 C 贪心 D 回溯

正确答案:C 本题考查算法设计与分析的基础知识。根据题干描述，每次在未被覆盖的房子中选择最左端的房子，在其右侧20米处(覆盖范围)安装消防栓。这是典型的贪心策略求解问题的思路。因此算法设计采用的是贪心策略。在求解过程中，只需要遍历一次房子即可，因此算法的时间复杂度为O(n)题干中的案例可以按如下图方式安装消防栓，黑点表示房子，圆圈表示消防栓的覆盖范围。

由上图可见，安装5个消防栓就可以覆盖这10栋房子。对于得到一个最优解是动态规划的特点，可以得到问题所有的最优解，是回溯法的特征，可以排除A、B选项。选择C。有些实例，可能得不到最优解。

采用Dijkstra算法求解下图A点到E点的最短路径，采用的算法设计策略是()。该最短路径的长度是 ()

A 分治法 B 动态规划 C 贪心算法 D 回溯法

A 5 B 6 C 7 D 9

正确答案:C A 答案解析:Diikstra算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到起始点距离最近且未访问过的顶点的邻接节点，真到扩展到终点为止。采田Diikstra算法，步骤如下:第一轮，从原始结点A出发，计算邻接结点的最短距离，B6，C1，D2，已计算结点的集合是(A)，未计算结点的集合是B，C，D，FL第二轮，从邻接结点出发，计算邻接的邻接，E从B出发是9，从C出发是7，取最小值7:同理F取最小值4。已计算结点的集合是ÍA，B，C，D)，未计算结点的集合是fF。第三轮，再从上一轮结点出发计算，得到E5。未计算结点的集合为空，至此，从A出发经所有节点到E结点的路径都已计算过，算法结束。

考虑下述背包问题的实例。有5件物品，背包容量为100，每件物品的价值和重量如下所示，并已经按照物品的单位重量价值从大到小排好序。根据物品单位重量价值大优先的策略装入背包中，则采用了(54)设计策略。考虑0/1背包问题(每件物品或者全部装入背包或者不装入背包)和部分背包问题(物品可以部分装入背包)，求解该实例得到的最大价值分别为( 55)。

物品编号	价值	重量	单位重量价值（这是自己计算的）
1	50	5	10
2	200	25	8
3	180	30	6
4	225	45	5
5	200	50	4

A 分治 B 贪心 C 动态规划 D 回溯

A 605和630 B 605和605 C 430和630 D 630和430

正确答案:B C 答案解析: 贪心算法(又称贪婪算法)是指，在对问题求解时，总是做出在当前看来是最好的选择。即，不在整体最优上加以考虑，它所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解但对范围相当广泛的许多问题他可能产生整体最优解或整体最优解的近似解。采用0/1背包考虑该问颖时,只能放入1,2,3号物品，所以总价值是430，采用部分背包可以将物品拆分，所以放入1,2,3号物品后还可以将编号4的物品部分的装入，使得背包容量尽量满，所以总容量是630。本题选择B选项。

🔹部分背包问题（物品可以切割）

使用贪心策略，优先选单位重量价值高的：

1. 选物品1：重量5，占用5，剩余容量95，总价值=50

2. 选物品2：重量25，占用25，剩余容量70，总价值=50+200=250

3. 选物品3：重量30，占用30，剩余容量40，总价值=250+180=430

4. 选物品4：重量45，只能装 40/45 = 8/9，价值=225×(40/45)=200，总价值=430+200=630

➡️ 部分背包最大价值 = 630

采用贪心策略求解( )问题,34、，一定可以得到最优解。

A 分数背包 B 0-1 背包 C 旅行商 D 最长公共子序列

正确答案:A 答案解析:贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。分数背包即部分背包问题，物品可选择部分或全部放进背包，直至装满背包，通过贪心算法求解可将放入单位价值最大的物品优先放入背包，以实现背包物品价值的最大化:0-1背包指物品整体放入或不放入背包，因此不一定能完全装满背包，采用贪心算法可以取得局部最优解，但不一定是全局最优解;旅行商问题是指旅行商要到若干个城市旅行，每访问一个城市后都会回到最初开始的城市，用贪心法不一定能求得最优解:最长公共子序列用贪心法也不一定能求得最优解:

回溯法⭐

概念：有“通用的解题法”之称，可以系统地搜索一个问题的所有解或任一解。在包含问题的所有解的解空间树中，按照深度优先的策略，从根节点出发搜索解空间树。搜索至任一结点时，总是先判断该结点是否肯定不包含问题的艇如果不包含，则跳过对以该结点为根的子树的搜索，逐层向其祖先结点回溯;否则，进入该子树，继续按深度优先的策略进行搜索。

可以理解为先进行深度优先搜索，一直向下探测，当此路不通时，返回上一层探索另外的分支，重复此步骤，这就是回溯，意为先一直探测，当不成功时再返回上一层。一般用于解决迷宫类的问题

要求“皇后”之间不能发生冲突，即任何两个“皇后”不能在同一行、同一列和相同的对要在8x8的棋盘上摆放8个“皇后”8角线上，则一般采用来实现。

A 分治法 B 动态规划法 C 贪心法 D 回溯法

正确答案:D 答案解析: N-皇后问题是一个经典的计算问题，该问题基于一些约束条件来求问题的可行解。该问题不易划分为子问题求解，因此分治法不适用;由于不是要求最优解，因此不具备最优子结构性质，也不宜用动态规划法和贪心法求解。而系统搜索法--回溯法可以有效地求解该问题。

分支限界法

原理：在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程这个过程一直持续到找到所需的解或活结点表为空时为止。

与回溯法的区别

• 求解目标是找出满足约束条件的一个解，或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解，即在某种意义下的最优解。

• 以广度优先或以最小耗费(最大收益)优先的方式搜索解空间树。

从活节点表中选择下一个扩展节点的类型

1. 队列式(FIFO)分支限界法：按照队列先进先出(FIFO)原则选取下一个节点为扩展节点。

2. 优先队列式分支限界法：按优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

概率算法

原理：在算法执行某些步骤时，可以随机地选择下一步该如何进行，同时允许结果以较小的概率出现错误，并以此为代价，获得算法运行时间的大幅度减少(降低算法复杂度)

基本特征是对所求解问题的同一实例用同一概率算法求解两次，可能得到完全不同的效果

如果一个问题没有有效的确定性算法可以在一个合理的时间内给出解，但是该问题能接受小概率错误，那么采用概率算法就可以快速找到这个问题的解。

四类概率算法：数值概率算法(数值问题的求解)、蒙特卡洛算法(求问题的精确解)、拉斯维加斯算法(不会得到不正确的解)、舍伍德算法(总能求得问题的一个正确解)。

概率算法的特征

1. 概率算法的输入包括两部分，一部分是原问题的输入，另一部分是一个供算法进行随机选择的随机数序列。

2. 概率算法在运行过程中，包括一处或多处随机选择，根据随机值来决定算法的运行路径。

3. 概率算法的结果不能保证一定是正确的，但能限制其出错概率。

4. 概率算法在不同的运行过程中，对于相同的输入实例可以有不同的结果因此，对于相同的输入实例，概率算法的执行时间可能不同。

近似算法

原理：解决难解问题的一种有效策略，其基本思想是放弃求最优解，而用近似最优解代替最优解，以换取算法设计上的简化和时间复杂度的降低。

虽然它可能找不到一个最优解，但它总会给待求解的问题提供一个解为了具有实用性，近似算法必须能够给出算法所产生的解与最优解之间的差别或者比例的一个界限，它保证任意一个实例的近似最优解与最优解之间的相差程度。显然，这个差别越小，近似算法越具有实用性。

衡量近似算法性能两个标准

1. 算法的时间复杂度。近似算法的时间复杂度必须是多项式阶，的这是近似算法的基本目标。

2. 解的近似程度。近似最优解的近似程度也是设计近似算法的重要目标。近似程度与近似算法本身、问题规模，乃至不同的输入实例有关。

数据挖掘算法

分析爆炸式增长的各类数据的技术，以发现隐含在这些数据中的有价值的信息和知识。数据挖掘利用机器学习方法对多种数据进行分析和挖掘。其核心是算法，主要功能包括分类、回归、关联规则和聚类等

分类

1. 是一种有监督的学习过程，根据历史数据预测未来数据的模型。

2. 分类的数据对象属性:一般属性、分类属性或目标属性

3. 分类设计的数据:训练数据集、测试数据集、未知数据。

4. 数据分类的两个步骤：学习模型(基于训练数据集采用分类算法建立学习型)、应用模型(应用测试数据集的数据到学习模型中，根据输出来评估模型的好坏以及将未知数据输入到学习模型中，预测数据的类型)

5. 分类算法:决策树归纳(自顶向下的递归树算法)、朴素贝叶斯算法、后向传播BP、支持向量机SVM。

频繁模式和关联规则挖掘

1. 挖掘海量数据中的频繁模式和关联规则可以有效地指导企业发现交叉销售机会、进行决策分析和商务管理等。(沃尔玛-啤酒尿布故事)

2. 首先要求出数据集中的频繁模式，然后由频繁模式产生关联规则。

3. 关联规则挖掘算法:类Apriori算法、基于频繁模式增长的方法如FP-growthh，使用垂直数据格式的算法，如ECLAT。

聚类

1. 是一种无监督学习过程。根据数据的特征，将相似的数据对象归为一类，不相似的数据对象归到不同的类中。物以类聚，人以群分。

2. 典型算法:基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法、基于统计模型的方法。

3. 数据挖掘的应用：数据挖掘在多个领域已有成功的应用。在银行和金融领域可以进行贷款偿还预测和顾客信用政策分析、针对定向促销的顾客分类与聚类洗黑钱和其他金融犯罪侦破等;在零售和电信业，可以进行促销活动的效果分析、顾客忠诚度分析、交叉销售分析、商品推荐、欺骗分析

智能优化算法

1. 优化技术是一种以数学为基础，用于求解各种工程问题优化解的应用技术。人工神经网络ANN:一个以有向图为拓扑结构的动态系统，通过对连续或断续的输入作状态响应而进行信息处理。从信息处理角度对人脑神经元网络进行抽象，建立某种简单模型，按不同的连接方式组成不同的网络。

2. 遗传算法:源于模拟达尔文的“优胜劣汰、适者生存”的进化论和孟德尔.摩根的遗传变异理论，在迭代过程中保持已有的结构，同时寻找更好的结构。其本意是在人工适应系统中设计一种基于自然的演化机制。

3. 模拟退火算法SA:求解全局优化算法。基本思想来源于物理退火过程，包括三个阶段:加温阶段、等温阶段、冷却阶段。将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

4. 禁忌搜索算法TS:模拟人类智力过程的一种全局搜索算法，是对局部邻域搜索的一种扩展。从一个初始可行解出发，选择一系列的特定搜索方向(移动)作为试探，选择实现让特定的目标函数值变化最多的移动。为了避免陷入局部最优解，TS搜索中采用了一种灵活的“记忆”技术，对已经进行的优化过程进行记录和选择，指导下一步的搜索方向，这就是Tabu表的建立。

蚁群算法

1. 是一种用来寻找优化路径的概率型算法。

2. 单个蚂蚁的行为比较简单，但是蚁群整体却可以体现一些智能的行为。例如蚁群可以在不同的环境下，寻找最短到达食物源的路径。这是因为蚁群内的蚂蚁可以通过某种信息机制实现信息的传递。后又经进一步研究发现，蚂蚁会在其经过的路径上释放一种可以称之为“信息素”的物质，蚁群内的蚂蚁对“信息素”具有感知能力，它们会沿着“信息素”浓度较高路径行走，而每只路过的蚂蚁都会在路上留下“信息素”，这就形成一种类似正反馈的机制，这样经过一段时间后，整个蚁群就会沿着最短路径到达食物源了

3. 用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多，随着时间的推进较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。

粒子群优化算法PSO

1. 设想这样一个场景：一群鸟在随机搜索食物。在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

2. PSO从这种模型中得到启示并用于解决优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

3. PSO 初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个"极值"来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。