opengl-变换&坐标系统
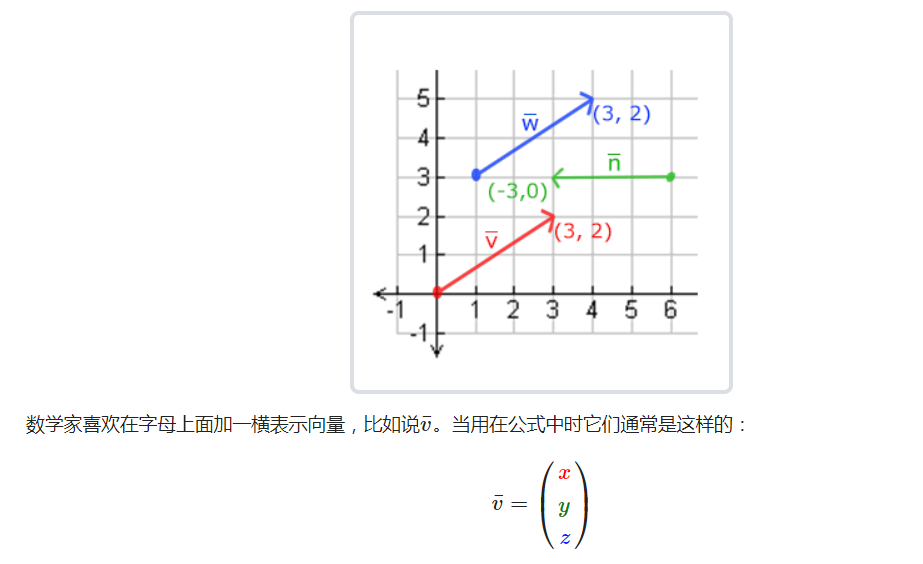
向量
定义: 向量是一个既有大小又有方向的量(联系位移和速度的概念)
理解向量把握:
- 向量的大小就是向量的长度(模),向量的长度非负
- 向量的方向描述了向量的指向
- 向量是没有位置的,与点是不同的
- 向量与标量不同,变量是只有大小而没有方向的量,例如位移是向量,而距离是标量
向量与标量运算
标量(Scalar) 只是一个数字(或者说是仅有一个分量的向量)。当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
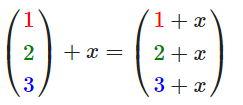
向量取反
对一个 向量取反(Negate) 会将其 方向逆转
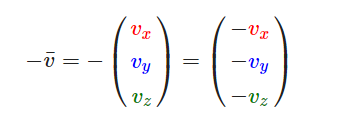
向量加减
向量的加法 可以被定义为是 分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量
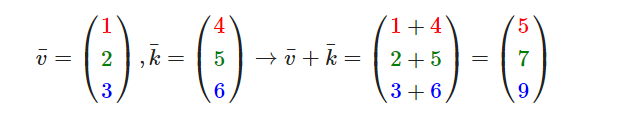
向量的减法 等于加上第二个向量的 相反向量
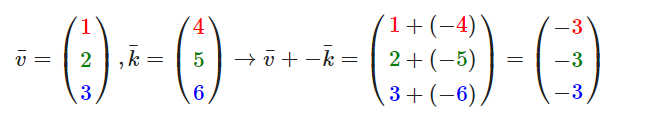
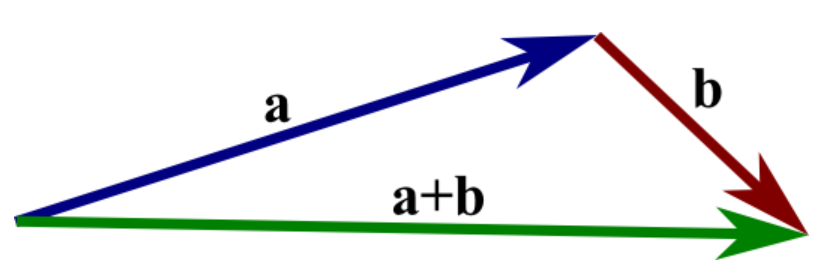
三角形法则
长度
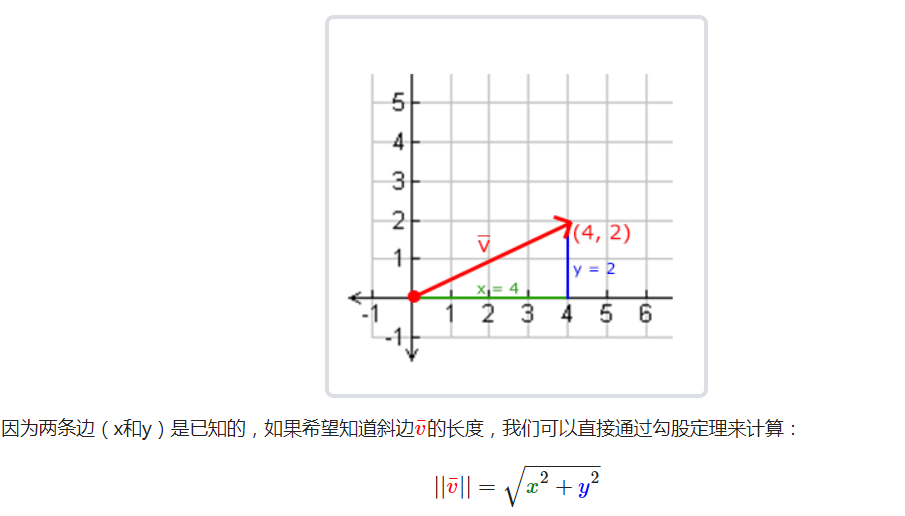
** 单位向量(Unit Vector)** : 单位向量有一个特别的性质——它的长度是1
任意向量的每个分量除以向量的长度得到它的单位向量n:
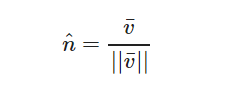
我们把这种方法叫做一个 向量的标准化(Normalizing)。单位向量头上有一个^样子的记号,通常单位向量会变得很有用,特别是在我们只关心方向不关心长度的时候(如果改变向量的长度,它的方向并不会改变)。
向量点乘
点积有两种定义方式:代数方式 和 **几何方式 **
代数定义
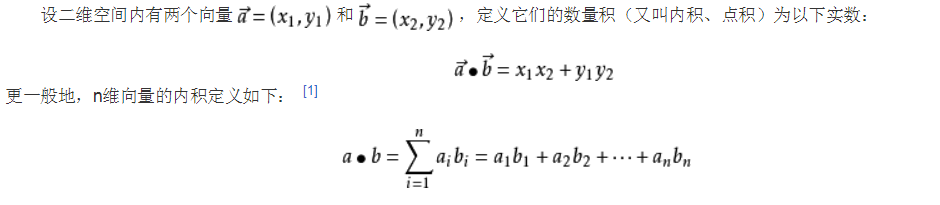
几何定义

应用:
使用点乘可以很容易测试两个向量是否 正交(Orthogonal) 或 平行(正交意味着两个向量互为直角);
可以快速计算出两个向量的 夹角

叉乘
叉乘只在 3D空间 中有定义,它需要两个 不平行向量 作为输入,生成一个 正交 于两个输入向量的第三个向量

注意叉乘结果的方向需要根据 右手规则 来确定。所谓右手规则是指,将向量a与b放在同一个起点时,当右手的四个手指从a所指方向转到b所指方向握拳时,大拇指的指向即为a×b的方向

几何意义
叉乘的模可以视为以a和b为两边的平行四边形的面积,
|A x B| = |A||B|Sin(θ)
其中|b|sinθ可以视为平行四边形的高,计算后a×b的模即为平行四边形的面积
矩阵的概念

行向量和列向量

矩阵加减法

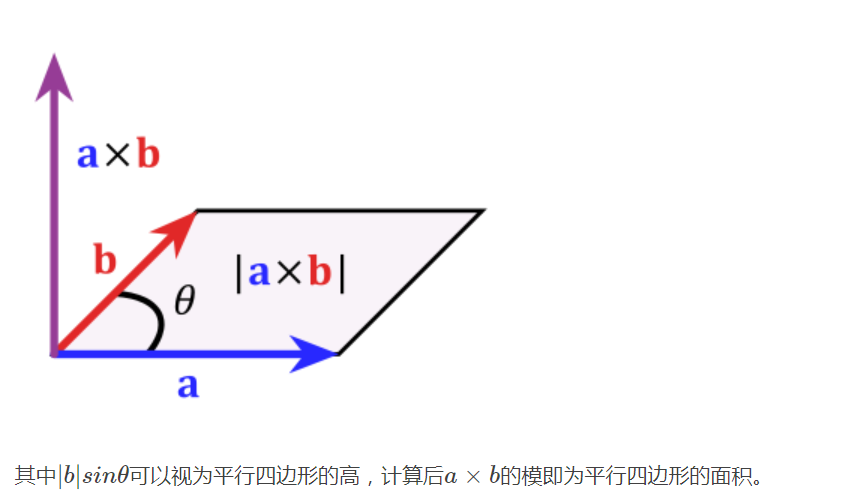
标量和矩阵乘法
矩阵和矩阵乘法

注意矩阵乘法不满足交换律 一般而言矩阵乘积AB≠BA(当然存在特殊情况下满足,逆矩阵相乘为单位矩阵),因此在OpenGL中应用变换矩阵时注意变换应用的顺序。
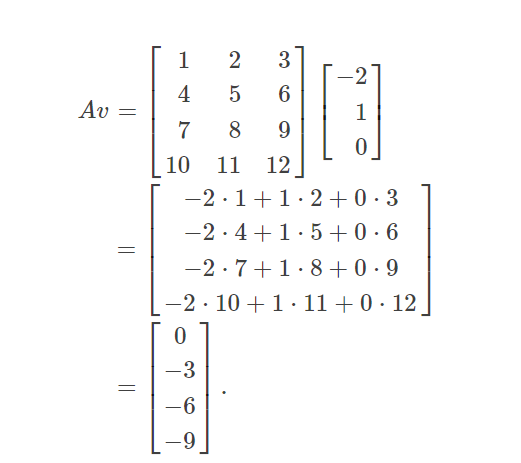
矩阵与向量相乘
矩阵和向量相乘是矩阵和矩阵相乘的特例,给定矩阵A和列向量v
单位矩阵
单位矩阵是一个除了对角线以外都是0的 N×N 矩阵
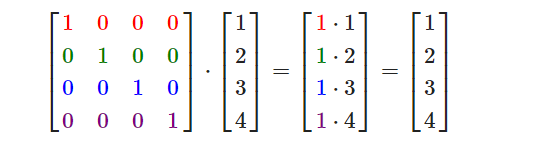
缩放
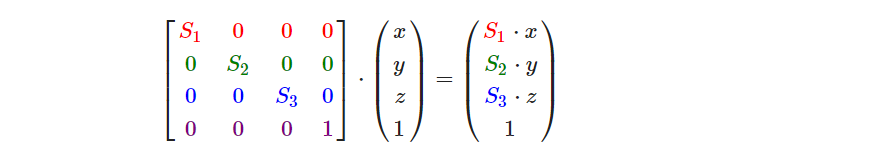
位移
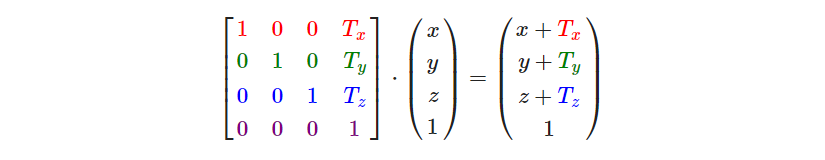
齐次坐标(Homogeneous Coordinates)
向量的w分量也叫 齐次坐标 。想要从齐次向量得到3D向量,我们可以把x、y和z坐标分别除以w坐标。我们通常不会注意这个问题,因为w分量通常是1.0。使用齐次坐标有几点好处:它允许我们在3D向量上进行位移(如果没有w分量我们是不能位移向量的),而且下一章我们会用w值创建3D视觉效果。
如果一个向量的齐次坐标是0,这个坐标就是方向向量(Direction Vector),因为w坐标是0,这个向量就不能位移(译注:这也就是我们说的不能位移一个方向)。
向量和点在同一个基下有不同的表达:3D向量的第4个代数分量是0,而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。
https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
旋转
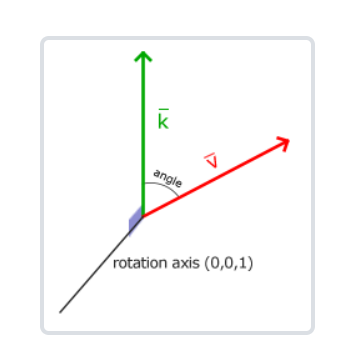
在3D空间中旋转需要定义一个 角 和一个 旋转轴(Rotation Axis)。物体会沿着给定的旋转轴旋转特定角度

万能公式
其中(Rx,Ry,Rz)代表任意旋转轴:
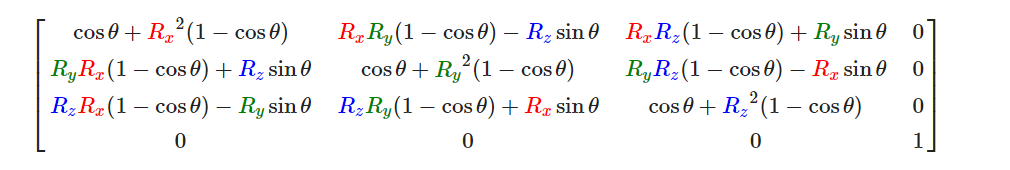
旋转矩阵推导https://blog.youkuaiyun.com/u012763833/article/details/52605747
实践
GLM
GLM是OpenGL Mathematics的缩写,它是一个 只有头文件 的库,拥有绝大多数的矩阵操作功能
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;
glm::mat4 trans;
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));
把矩阵传递给着色器
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
}
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
- 第一个参数,它是uniform的位置值
- 第二个参数告诉OpenGL我们将要发送多少个矩阵,这里是1
- 三个参数询问我们我们是否希望对我们的矩阵进行置换(Transpose),OpenGL开发者通常使用一种内部矩阵布局,叫做列主序(Column-major Ordering)布局。GLM的默认布局就是列主序
- 最后一个参数是真正的矩阵数据,矩阵首地址





















 1612
1612

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








