组合逻辑电路（一）（加法器）_加法器逻辑电路-优快云博客

本文链接：https://blog.youkuaiyun.com/qwertf123/article/details/135981267

目录

组合逻辑电路的特点及功能描述

采用SSI的组合逻辑电路的分析与设计

采用SSI的组合逻辑电路的分析

采用SII的组合逻辑电路的设计

例

例

例

常用的MSI组合逻辑电路

半加器

全加器

加法器

串行进位加法器

例

例

超前进位加法器

组合逻辑电路的特点及功能描述

小规模集成电路（SSI）：一个封装内部的逻辑门个数小于12个的集成电路

中规模集成电路（MSI）：一个封装内部有12~100个等效逻辑门的集成电路

组合逻辑电路在逻辑功能上的特点是：电路在任何时刻的输出状态仅仅取决于该时刻电路输入信号的状态，而与电路原有的状态无关，没有记忆功能

组合逻辑电路在结构上的特点是：由各种门电路构成，不含存储元件

采用SSI的组合逻辑电路的分析与设计

采用SSI的组合逻辑电路的分析

分析步骤

写输出逻辑函数表达式

根据给出的逻辑电路，从输入到输出或从输出到输入逐级写出各级门电路的输出逻辑函数式，合并整理

逻辑函数化简或变换

利用公式化简法或卡诺图化简法将得到的表达式化简或变换，求出最简逻辑函数式

列真值表

将输入变量的各种取值组合（通常按二进制数递增顺序排列）代入输出逻辑函数式进行计算，求出相应的输出函数值，并一一对应地列出真值表

说明电路功能逻辑

根据化简后的输出逻辑函数表达式或真值表说明电路的逻辑功能

采用SII的组合逻辑电路的设计

设计步骤

列真值表

首先根据命题分析事件的因果关系，确定输入变量和输出变量，一般把事件的起因定为输入变量，把事件的结果作为输出变量，然后对逻辑变量进行赋值

所谓逻辑赋值，就是用二值逻辑的0、1分别表示输入变量和输出变量的两种不同状态，最后根据输出和输入变量之间的因果关系列出真值表

写输出逻辑函数式

将真值表中输出逻辑函数值为1所对应的各个最小项进行逻辑加，便得到输出逻辑函数的最小项表达式

逻辑函数化简或变换

逻辑函数化简或变换与选择的器件型号有关

为了获得简单的设计结果，通常采用卡诺图法或代数法对逻辑函数进行化简

当所用器件的种类有所限制时，则要将函数表达式变换成与器件种类相适应的形式

画逻辑电路图

根据化简或变换后的逻辑函数表达式画出逻辑电路图

例

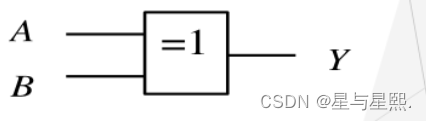
分析电路的逻辑功能

解

本题有两个输入变量A和B，一个输出变量F

出现了三种逻辑符号

非逻辑

与非逻辑

与逻辑

对于A输入变量上边与B非相与非，为 $\overline{A\bar{B}}$

对于B输入变量下边与A非相与非，为 $\overline{B\bar{A}}$

最后相与 $F=\overline{A\bar{B}}\cdot \overline{B\bar{A}}$

化简一：

$F=\overline{A\bar{B}}\cdot \overline{B\bar{A}}$

$=(\bar{A}+B)\cdot (\bar{B}+A)$

$=\bar{A}\bar{B}+\bar{A}A+\bar{B}B+AB$

$=\bar{A}\bar{B}+AB$

$=A\bigodot B$
化简二：

$F=\overline{A\bar{B}}\cdot \overline{B\bar{A}}$

$=\overline{A\bar{B}+B\bar{A}}$

$=\overline{A\bigoplus B}$

$=A\bigodot B$
所以电路实现同或的逻辑功能

例

分析电路的逻辑功能

解

本题有五个输入变量B，A0，A1，A2和A3，四个输出变量S0，S1，S2和S3

出现了一个逻辑符号

异或逻辑

当输入变量B为0时，0与1异或为1，0与0异或为0

即不管A输入变量输入的是什么，对应的输出变量都是A输入的，即为原码输出

当输入变量B为1时，1与0异或为1，1与1异或为0

即不管A输入变量输入的是什么，对应的输出变量都与A输入的相反，即反码输出

所以该电路为原码/反码的发生器

例

写出所示电路的逻辑表达式，并化简为最简与或表达式

解

本题有三个输入变量A，B和C，两个输出变量Y0和Y1

出现了两个逻辑符号

与非逻辑

异或逻辑

对于Y0输出变量，连接一个异或符号

A与B异或后与C异或后输出Y0

即

$Y_{0}=A\bigoplus B\bigoplus C$

对于Y1输出变量，连接一个与非

之后再分别连接两个与非

对于第一个与非为 $\overline{AB}$

对于第二个与非为 $\overline{C(A\bigoplus B)}$

即

$Y_{1}=\overline{\overline{AB}\cdot \overline{C(A\bigoplus B)}}$

化简

$Y_{1}=AB+C(A\bigoplus B)$
此电路图为全加器

Y0为计算本位和的公式，Y1为计算进位的公式

在下面会详细解释

常用的MSI组合逻辑电路

串行进位：电路进行二进制加法运算时，各全加器由低位到高位逐位传递进位信号

超前进位：电路进行二进制加法运算时，通过快速进位电路几乎同时产生进位信号

半加器

只考虑本位两个二进制数相加，而不考虑来自低位进位数相加的运算电路

假设两个1位二进制数A和B相加，S为A和B相加的和，C为进位输出

半加器真值表
A B S C
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1

半加器逻辑符号：
A加数 B被加数 S本为和 CO进位

半加器真值表
A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

全加器

将两个多位二进制数相加时，除考虑第i位两个二进制数 $A_{i}$ 和 $B_{i}$ 相加外，还要考虑与相邻低位来的进位数 $C_{i}$ 相加的运算电路，称为全加器

两个二进制数相加的结果有两个，一个是第i位的和 $S_{i}$ ，另一个是向相邻高位的进位数 $C_{i+1}$

因此，全加器有三个输入端，两个输出端

1位全加器真值表
输入输出

$A_{i}$ $B_{i}$ $C_{i}$ $S_{i}$ $C_{i+1}$
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
由真值表得到全加器的逻辑表达式为
$S_{i}=\bar{A_{i}}\bar{B_{i}}C_{i}+\bar{A_{i}}B_{i}\bar{C_{i}}+A_{i}\bar{B_{i}}\bar{C_{i}}+A_{i}B_{i}C_{i}$
$=(\bar{A_{i}}\bar{B_{i}}+A_{i}B_{i})C_{i}+(A_{i}\bar{B_{i}}+\bar{A_i}B_{i})\bar{C_{i}}$
$=A_{i}\bigoplus B_{i}\bigoplus C_{i}$

$C_{i+1}=\bar{A_{i}}B_{i}C_{i}+A_{i}\bar{B_{i}}C_{i}+A_{i}B_{i}\bar{C_{i}}+A_{i}B_{i}C_{i}$
$=A_{i}B_{i}+C_{i}(A_{i}\bigoplus B_{i})$

1位全加器真值表
输入	输出

加法器

实现多位二进制数加法运算的电路称为加法器

按照电路结构及进位方式的不同，分为串行进位加法器和超前进位加法器

串行进位加法器

一个全加器只能进行两个1位二进制数相加

因此，当进行多位二进制数相加时，就必须使用多个全加器才能完成

n位串行进位加法器逻辑图：

例

如图所示串行进位加法器当A=11，B=01时，高位的进位输出端为1

解

本题有五个输入变量C0，A0，B0，A1和B1

C0为初始进位，为0

A=A0A1=11 即A0输入1，A1输入1

B=B0B1=01 即B0输入0，B1输入1

高位即最后一个

低位即第一个

方法一：

利用公式

$S_{i}=A_{i}\bigoplus B_{i}\bigoplus C_{i}$

$C_{i+1}=A_{i}B_{i}+C_{i}(A_{i}\bigoplus B_{i})$

$S_{0}=A_{0}\bigoplus B_{0}\bigoplus C_{0}$

$=1\bigoplus 1\bigoplus 0$

$=0$
$C_{1}=A_{0}B_{0}+C_{0}(A_{0}\bigoplus B_{0})$

$=1\cdot 1+0\cdot (1\bigoplus 1)$

$=1$

$S_{1}=A_{1}\bigoplus B_{1}\bigoplus C_{1}$

$=1\bigoplus 0\bigoplus 1$

$=0$

$C_{2}=A_{1}B_{1}+C_{1}(A_{1}\bigoplus B_{1})$

$=1\cdot 0+1\cdot (1\bigoplus 0)$

$=1$
所以高位输出端为1

方法二：

此逻辑图用于计算二进制加法

即第一次A0=1，B0=1，C0=0

同十进制加法的进位和加减规则

A0+B0+C0=1+1+0=10

10中即进位C1为1，本位和S0=0

第二次A1=1，B1=0，C1=1

A1+B1+C1=1+0+1=10

10中即C2为1，本位和为S1=0

例

如下图所示，当输入A为0101，B为1001时，S2=1

解

A=A3A2A1A0=0101

即A3=0，A2=1，A1=0，A0=1

B=B3B2B1B0=1001

即B3=1，B2=0，B1=0，B0=1
方法一：

利用公式

$S_{i}=A_{i}\bigoplus B_{i}\bigoplus C_{i}$

$C_{i+1}=A_{i}B_{i}+C_{i}(A_{i}\bigoplus B_{i})$

$S_{0}=A_{0}\bigoplus B_{0}\bigoplus C_{0}$

$=1\bigoplus 1\bigoplus 0$

$=0$
$C_{1}=A_{0}B_{0}+C_{0}(A_{0}\bigoplus B_{0})$

$=1\cdot 1+0\cdot (1\bigoplus 1)$

$=1$

$S_{1}=A_{1}\bigoplus B_{1}\bigoplus C_{1}$

$=0\bigoplus 0\bigoplus 1$

$=1$

$C_{2}=A_{1}B_{1}+C_{1}(A_{1}\bigoplus B_{1})$

$=0\cdot 0+1\cdot (0\bigoplus 0)$

$=0$

$S_{2}=A_{2}\bigoplus B_{2}\bigoplus C_{2}$

$=1\bigoplus 0\bigoplus 0$

$=1$

方法二：

此逻辑图用于计算二进制加法

即第一次A0=1，B0=1，C0=0

A0+B0+C0=1+1+0=10

10中即进位为C1=1，本位和S0=0

第二次A1=0，B1=0，C1=1

A1+B1+C1=0+0+1=1

01中即进位为C2=0，本位和S1=1

第三次A2=1，B2=0，C2=0

A2+B2+C2=1+0+0=1

01中即进位为C3=0，本位和S2=1