目录
第1关:二叉树的实现之前序遍历
注意遍历顺序:先根结点,再左结点,再右结点
所以递归顺序也是先根结点,再左结点,再右结点
任务描述
树在计算机领域中有着广泛的应用,例如在编译程序中,用树来表示源程序的语法结构;在数据库系统中,数据的信息也是用树来组织的,以及操作系统中的目录结构。
本关任务:完成用二叉链表存储的二叉树的前序遍历算法。
相关知识
树
定义
树
(Tree)是n(n≥0)个结点的有限集合T,若n=0时称为空树,否则:
- 有且只有一个特殊的称为根
(root)结点;- 若
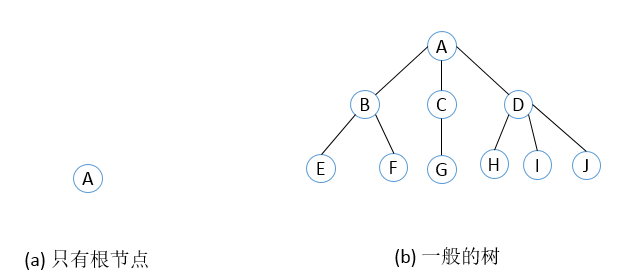
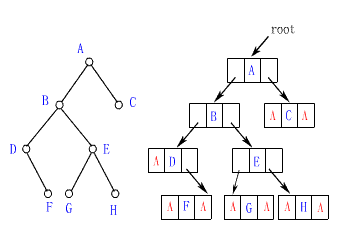
n>1时,其余的结点被分为m(m>0)个互不相交的子集T1,T2,T3...Tm,其中每个子集本身又是一棵树,称为根的子树。 这是树的递归定义,即用树来定义树。如下图所示:
树的基本术语
(1)结点的度 树中的一个结点拥有的子树数称为该结点的度。上图(b)中结点A的度是3,结点B的度是2,E的度是0。(2)孩子和双亲 树中某个结点的子树之根称为该结点的孩子或儿子,相应地,该结点称为孩子的双亲或父亲。同一个双亲的孩子称为兄弟。 上图(b)中结点B、C、D是结点A的子结点,而结点A是结点B、C、D的父结点。B、C、D的兄弟结点。(3)叶子结点 树中度为0的结点称为叶子结点,相应地,度不为0的结点为非叶子结点。E、F、G、H、I、J是叶子结点。(4)结点的层数和树的高度 结点的层数从根起算,根的层数为1,其余结点的层数等于其双亲结点的层数加1。树中结点的最大层数称为树的高度或深度。二叉树
二叉树的定义
二叉树是
n(n≥0)个结点的有限集,它或者是空集(n=0),或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。这是二叉树的递归定义。二叉树的五种基本形态
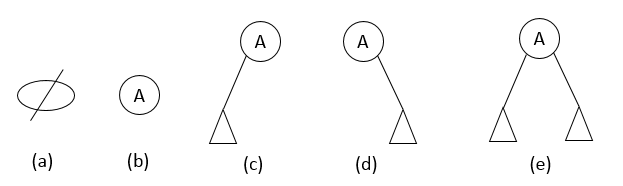
二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。 二叉树的五种基本形态如下图所示。
(a)空二叉树(b)仅有一个根结点的二叉树(c)右子树为空的二叉树(d)左子树为空的二叉树(e)左右子树均非空的二叉树满二叉树
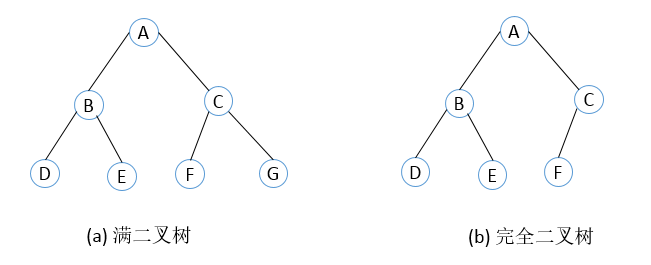
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
完全二叉树
若一棵二叉树至多只有最下面的两层上结点的度数可以小于
2,并且最下一层上的结点都集中在该层最左边的若干位置上,则此二叉树称为完全二叉树。
二叉树的存储结构
顺序存储结构
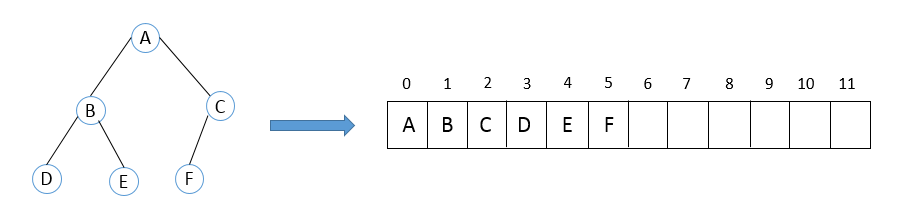
用一组地址连续的存储单元依次自上而下,从左至右存储二叉树上的结点元素。
这种方式仅适用完全二叉树,对于非完全二叉树,将会造成空间浪费。
链式存储结构
以链式方式存储二叉树。用链接方式存储二叉树时,因二叉树的每个结点最多有两个孩子,所以每个结点除了存储结点本身的数据外,还应设置两个指针域
lchild和rchild,分别指向该结点的左孩子和右孩子。结点的结构为:
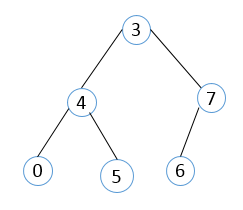
下图是二叉树的链式存储的一个实例图:
这里
root指向二叉树的根结点,若二叉树为空,则root==null;若结点的某个孩子不存在,则相应的指针为null。二叉树的遍历
所谓遍历,是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。
前序遍历
先序遍历是指遍历二叉树时,访问结点的操作发生在遍历其左右子树之前。 从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成,因此前序遍历的递归算法定义如下: 若二叉树非空,则:
(1)访问根结点;(2)遍历左子树;(3)遍历右子树。
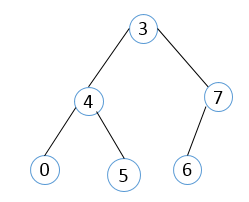
上图的前序遍历结果为:
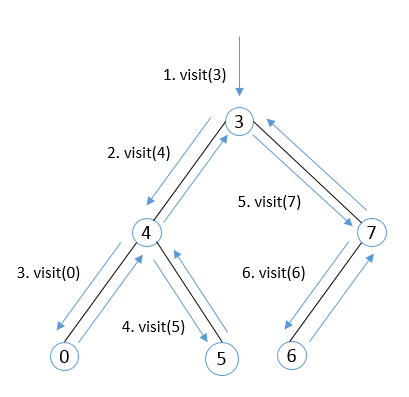
3 4 0 5 7 6。遍历次序示意图如下:
首先访问根结点
3,接着遍历其左子树,访问结点4,继续遍历结点4的左子树,访问结点0,因结点0的左右子树均为空,结束对结点4的左子树的遍历,返回遍历4的右子树,遍历完4的右子树后,继续遍历根结点3的右子树,直至所有结点访问完为止。
代码:
package step1;
/**
* Created by zengpeng on 2018/2/9.
*/
public class BinaryTree {
private TreeNode root;//根节点
public BinaryTree() {
root = null;
}
public void preOrder(TreeNode root) {
/********** Begin *********/
//先序遍历顺序,中左右
if(root==null)//如果根结点为空则直接返回,根结点为空即没有结点
return;//没有返回类型
System.out.println(root.item);//没递归之前为中间结点
//递归实现结点遍历
preOrder(root.leftChild);//中间结点的左结点,下次进入preOrder方法则输出此数,左结点
preOrder(root.rightChild);//中间结点的右结点,下次进入preOrder方法则输出此数,右结点
/********** End *********/
} //3 4 0 5 7 6
/**
*以数组arr的数据,依次从上至下,从左至右构建一颗二叉树
*
* @param arr
* @param n
* @return
*/
public TreeNode createTree(int arr[]) {
TreeNode tmp[] = new TreeNode[arr.length + 1];
for (int k = 1; k <= arr.length; k++) {
TreeNode node = new TreeNode(arr[k - 1]);
tmp[k] = node;
if (k == 1) {
root = node;
} else {
int j = k / 2;
if (k % 2 == 0) {
tmp[j].leftChild = node;
} else {
tmp[j].rightChild = node;
}
}
}
return root;
}
public static class TreeNode {
private TreeNode leftChild;
private TreeNode rightChild;
private int item;
public TreeNode(int item) {
this(null, null, item);
}
public TreeNode(TreeNode leftChild, TreeNode rightChild, int item) {
this.leftChild = leftChild;
this.rightChild = rightChild;
this.item = item;
}
}
}
以下是测试样例: 测试输入:
63 4 7 0 5 6预期输出:
340576
第2关:二叉树的实现之中序遍历
注意遍历顺序:先左结点,再根结点,再右结点
所以递归顺序也是先左结点,再根结点,再右结点
任务描述
在上一关,我们实现了二叉树的前序遍历,本关我们将实现二叉树的中序遍历。
本关任务:实现以二叉链表存储的二叉树的中序遍历算法。
相关知识
二叉树的相关知识请参考上一关。
二叉树的中序遍历
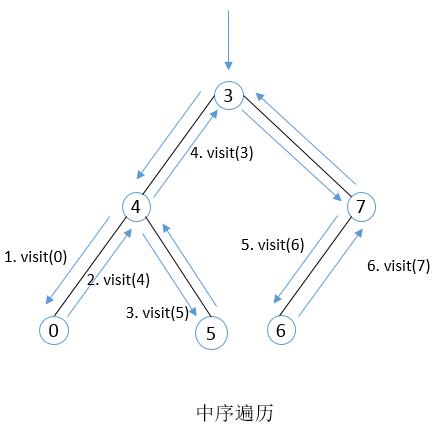
中序遍历二叉树时,对结点的访问次序为中序序列,即首先访问左子树,再访问根结点,最后访问右子树。
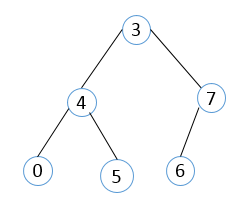
上图二叉树的中序遍历结果为:
0 4 5 3 6 7。中序遍历次序示意图如下:
中序遍历的递归算法定义如下: 若二叉树非空,则:
(1)遍历左子树;(2)访问根结点;(3)遍历右子树。
代码:
package step2;
/**
* Created by zengpeng on 2018/2/12.
*/
public class BinaryTree {
private TreeNode root;//根节点
public BinaryTree() {
root = null;
}
public void inOrder(TreeNode root) {
/********** Begin *********/
//中序遍历顺序,左中右
if(root==null)//如果根结点为空则直接返回,根结点为空即没有结点
return;//没有返回类型
//递归实现结点遍历
inOrder(root.leftChild);//中间结点的左结点,下次进入inOrder方法则输出此数,左结点
System.out.println(root.item);//输出
inOrder(root.rightChild);//中间结点的右结点,下次进入inOrder方法则输出此数,右结点
/********** End *********/
}
/**
* 以数组arr的数据,依次从上至下,从左至右构建一颗二叉树
*
* @param arr
* @param n
* @return
*/
public TreeNode createTree(int arr[]) {
TreeNode tmp[] = new TreeNode[arr.length + 1];
for (int k = 1; k <= arr.length; k++) {
TreeNode node = new TreeNode(arr[k - 1]);
tmp[k] = node;
if (k == 1) {
root = node;
} else {
int j = k / 2;
if (k % 2 == 0) {
tmp[j].leftChild = node;
} else {
tmp[j].rightChild = node;
}
}
}
return root;
}
public static class TreeNode {
private TreeNode leftChild;
private TreeNode rightChild;
private int item;
public TreeNode(int item) {
this(null, null, item);
}
public TreeNode(TreeNode leftChild, TreeNode rightChild, int item) {
this.leftChild = leftChild;
this.rightChild = rightChild;
this.item = item;
}
}
}
以下是测试样例:
测试输入:
63 4 7 0 5 6预期输出:
0 4 5 3 6 7
第3关: 二叉树的实现之后序遍历
注意遍历顺序:先左结点,再右结点,再根结点
所以递归顺序也是先左结点,再右结点,再根结点
任务描述
本关任务:实现以二叉链表存储的二叉树的后序遍历算法。
相关知识
二叉树的相关基础知识请参考上一关。
二叉树的后序遍历
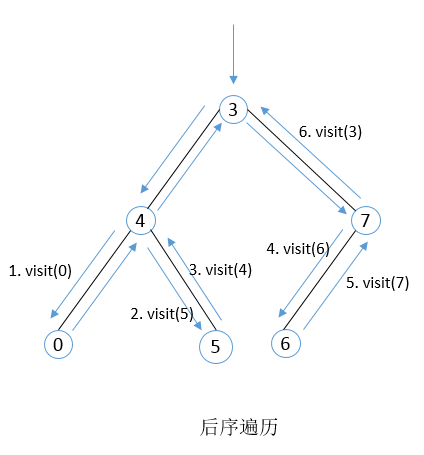
后序遍历是指在遍历二叉树时,先递归地打印结点的左子树、右子树,最后打印结点。对于下图:
其后序遍历结果为:
0 5 4 6 7 3。遍历示意图如下:
后序遍历的递归算法可表示如下: 若二叉树非空,则: (1) 遍历左子树; (2) 遍历右子树; (3) 访问根结点。
代码:
package step3;
/**
* Created by zengpeng on 2018/2/12.
*/
public class BinaryTree {
private TreeNode root;//根节点
public BinaryTree() {
root = null;
}
public void postOrder(TreeNode root) {
/********** Begin *********/
//后序遍历顺序,左右中
if(root==null)//如果根结点为空则直接返回,根结点为空即没有结点
return;//没有返回类型
//递归实现结点遍历
postOrder(root.leftChild);//中间结点的左结点,下次进入postOrder方法则输出此数,左结点
postOrder(root.rightChild);//中间结点的右结点,下次进入postOrder方法则输出此数,右结点
System.out.println(root.item);//输出
/********** End *********/
}
/**
* 以数组arr的数据,依次从上至下,从左至右构建一颗二叉树
*
* @param arr
* @param n
* @return
*/
public TreeNode createTree(int arr[]) {
TreeNode tmp[] = new TreeNode[arr.length + 1];
for (int k = 1; k <= arr.length; k++) {
TreeNode node = new TreeNode(arr[k - 1]);
tmp[k] = node;
if (k == 1) {
root = node;
} else {
int j = k / 2;
if (k % 2 == 0) {
tmp[j].leftChild = node;
} else {
tmp[j].rightChild = node;
}
}
}
return root;
}
public static class TreeNode {
private TreeNode leftChild;
private TreeNode rightChild;
private int item;
public TreeNode(int item) {
this(null, null, item);
}
public TreeNode(TreeNode leftChild, TreeNode rightChild, int item) {
this.leftChild = leftChild;
this.rightChild = rightChild;
this.item = item;
}
}
}
以下是测试样例:
测试输入:
63 4 7 0 5 6预期输出:
0 5 4 6 7 3























 1307
1307












