专题： 动态规划（递推关系）（53，62,63，64，72,91）

动态规划   一般解题框架

类型：

 

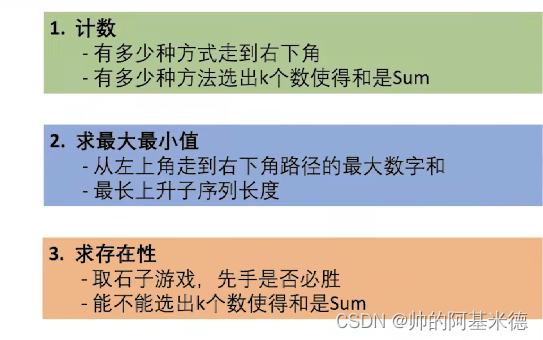
例题1

 

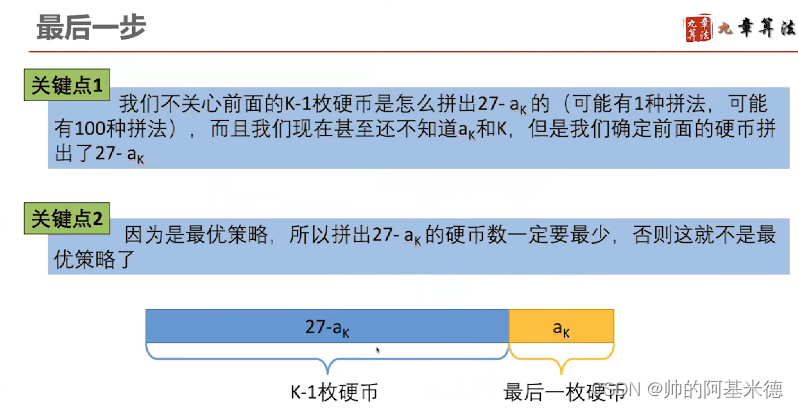
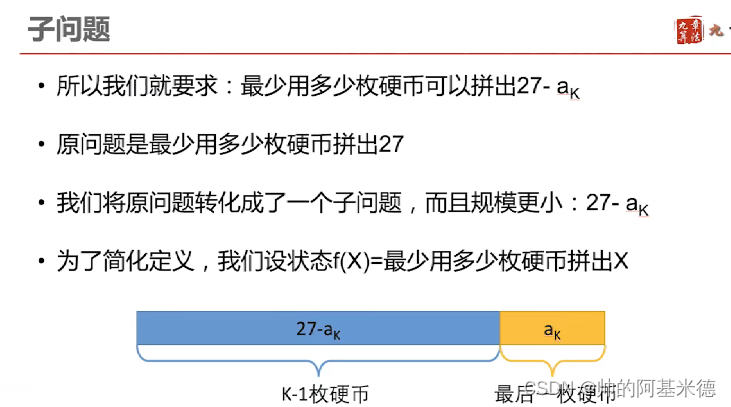
 动态规划：

 *   若存在一个状态不能从状态转移方程求得，但是又有值，就得手动设置初始值

 当 大值是有小值计算得到，就从小到大计算

 

  

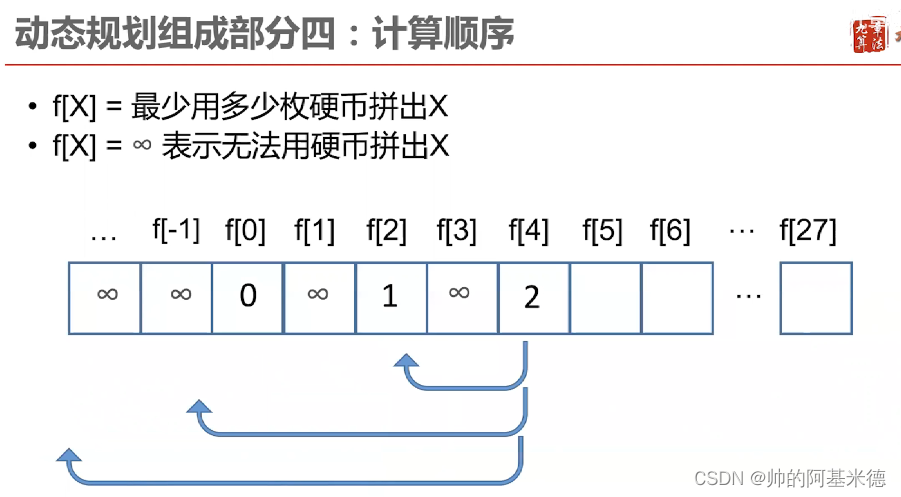
例题2     

 

 

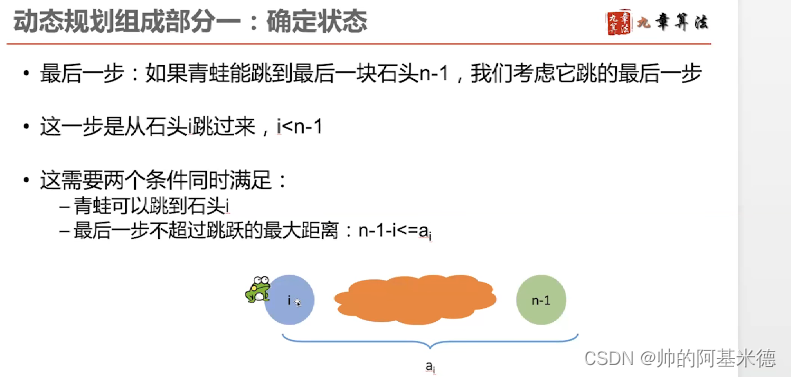
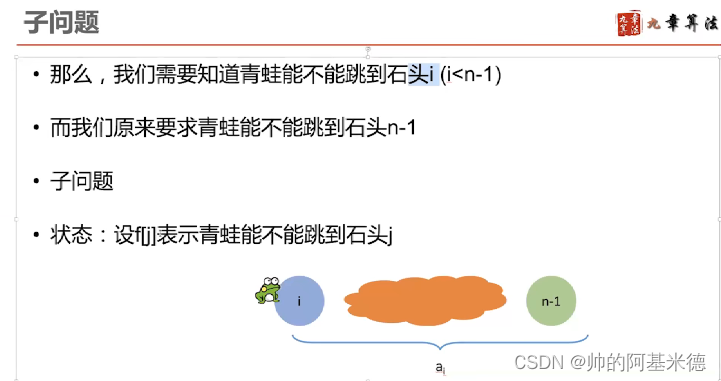
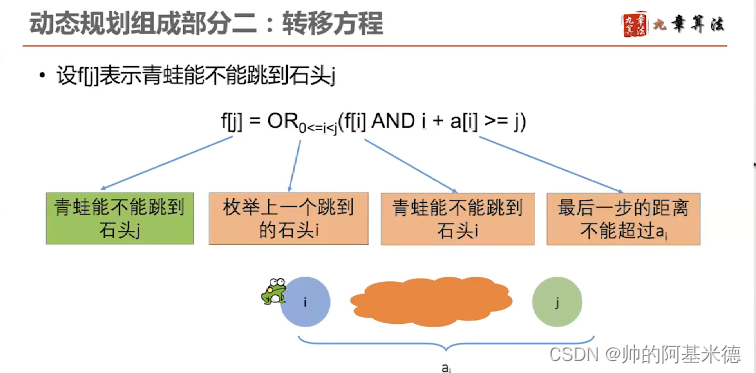
1.给定一个字符串S，找到S中最长的回文子串

 1. 1暴力解法：class Sotulation:  # 两层for  直接找

                              def   findmaxsubstr(self,s):

                                     maxlen=1

                                      begin=0 

                                      i=0

                                      for  i in range(0,len(s))   :

                                           for j in range(i+1,len(s)):

                                                   if   j-i+1>maxlen and Ifsubstr(i,j):         

                                                              maxlen=j-i+1

                                                               begin=i

                                        return s[begin:begin+maxlen]           

                                  def Ifsubstr(i,j):

                                           while i<j:

                                                  if s [i]!=s[j]:

                                                         return false

                                                   else:

                                                          i+=1

                                                           j-=1

                                                 return True  

1.2. 我的解法：

思路：只要j不过界，每次往后移，i 都从头开始判断。确定了区间内有回文后，需根据回文串长度的奇偶做不同处理。

2. 给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

• '.' 匹配任意单个字符

• '*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

。。。。。。不会

32  最长有效括号 ： 给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

 思想 ： 动态规划：首先确定 遇到右括号 才有可能是一对 格式正确的括号。最后一个位置 i 若是右括号，前面若是左括号，则在i-2位置的有效括号长度上+2；若i-1位置是右括号，则判断在i-1位置上的有效括号数之前的位置是否为左括号，若是，则与i位置上的匹配上  。  动态规划 需要根据提意定义一个数组dp，记录每个位置上的连续有效括号长度.

 

42 。 接雨水 ：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

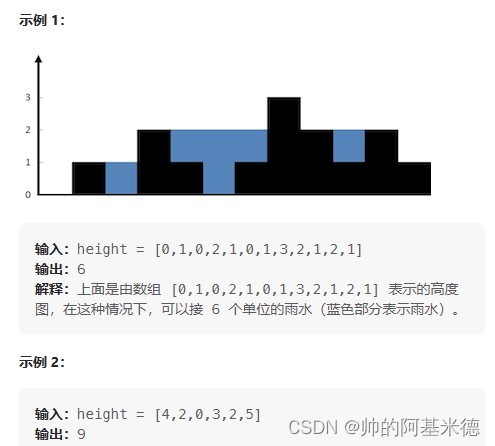
思想 动态规划（或双指针）

44 .（好题）通配符匹配。给你一个输入字符串 (s) 和一个字符模式 (p) ，请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配：

• '?' 可以匹配任何单个字符。
• '*' 可以匹配任意字符序列（包括空字符序列）。判定匹配成功的充要条件是：字符模式必须能够 完全匹配 输入字符串（而不是部分匹配）。

思想：  #重点在于  ： 用cache 记录下标位置；对于*，有需要时再用。

# p中遇到* 记录指针 在 s p的位置，先让* 后一位与S中当前字符匹配，若不匹配，就让* 代替一个；再让*后面与已被代替的后面字符匹配，若再不匹配，让* 代替两个，如此往后。(即 遇到 * 先不用，记下位置，若后面不能匹配了，在找他帮忙)

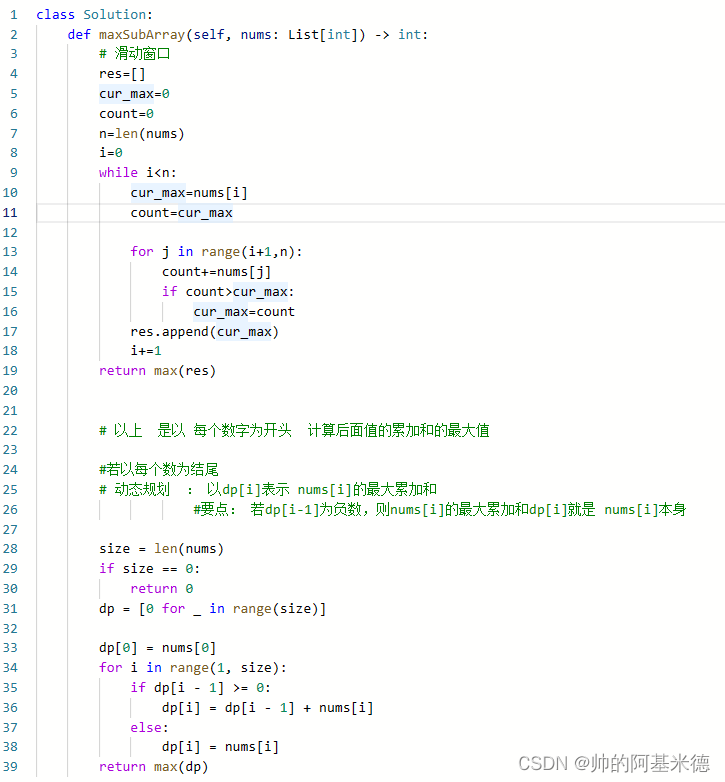
53 。 给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

思路：动态规划。 若 以双指针的方法，慢指针移动，快指针挨个遍历后面的值，记录 与以慢指针所指元素为开头的每个累加和；时间复杂度高；

动态规划思想，若以每个元素为一段序列的结尾，用dp[i] 记录以nums[i] 为结尾的最大累加和；

 

62 不同路径  .一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？

思想：  动态规划  ： 到最后位置 前，是在最后位置的左边或上面，所以到最后位置的路径为  到其左边路径总数+到其上面位置的路径总数；由此确定状态转移方程

  # 初始化开始情况，第一行第一列  的经过路径都是 1

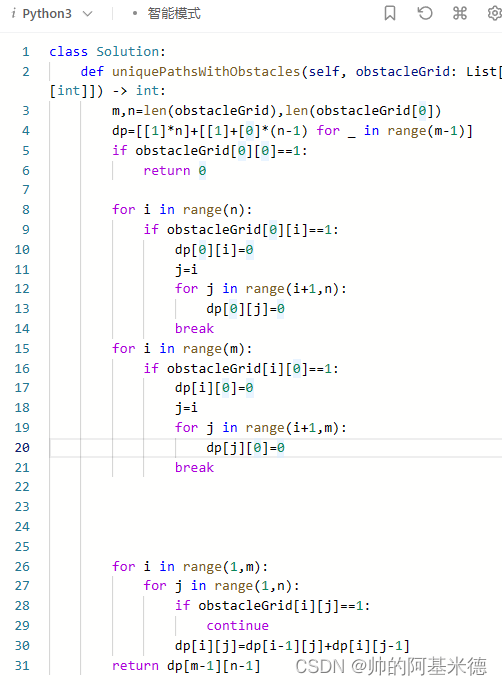
 63   不同路径 II 。一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

思想： 动态规划    ，  较上题，本题在路径中随机多了障碍。因此在构造 dp 时，要将障碍位置置为 0 ；若在第一行或第一列中有障碍， 则障碍及其后面都是0

 64 .   最小路径和. 给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

思想：动态规划。

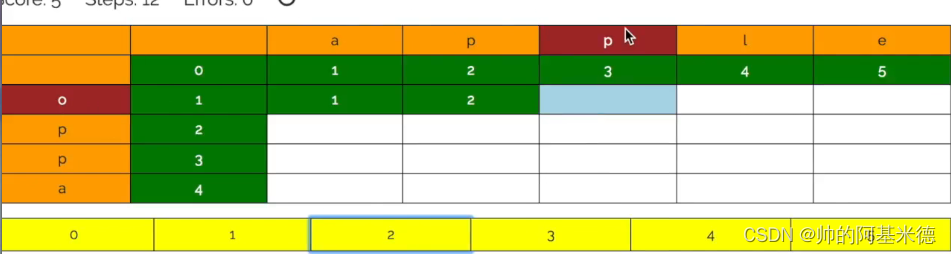
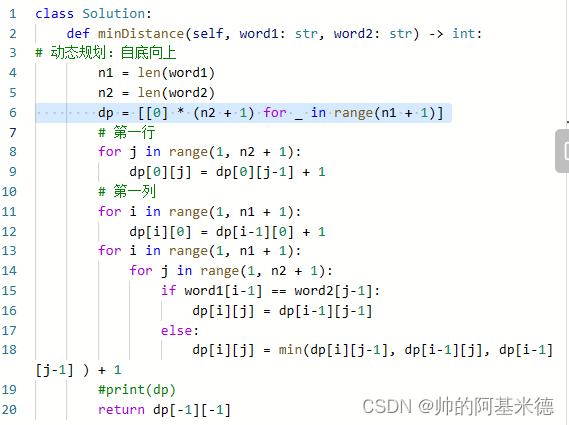
72 编辑距离。 给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

思想 ； 动态规划。 构建DP二维矩阵，初始化 第一行第一列。以第0列的a为例：a要变成空格，就得将其前面的三个都删除，再删除自己，所以要四步；

 

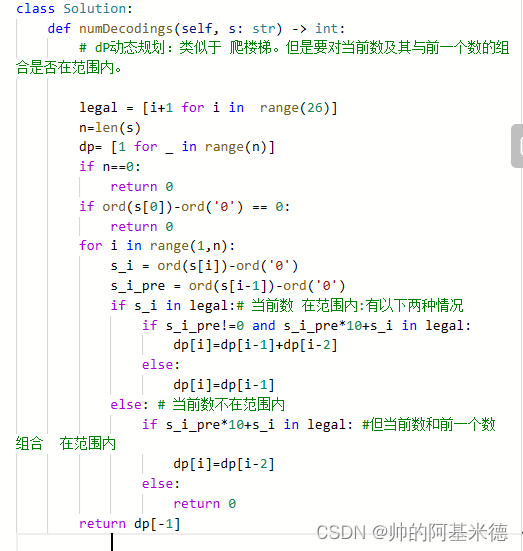
91 解码方法

一条包含字母 A-Z 的消息通过以下映射进行了 编码 ：

'A' -> "1"
'B' -> "2"
...
'Z' -> "26"

要 解码 已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，"11106" 可以映射为：

• "AAJF" ，将消息分组为 (1 1 10 6)
• "KJF" ，将消息分组为 (11 10 6)

注意，消息不能分组为  (1 11 06) ，因为 "06" 不能映射为 "F" ，这是由于 "6" 和 "06" 在映射中并不等价。

给你一个只含数字的 非空 字符串 s ，请计算并返回 解码 方法的 总数 。

题目数据保证答案肯定是一个 32 位 的整数。

思路： 大写A-Z对应着 "1"-"26" ,此处利用ord('0')=48.对于s 中的每一位，就算ord(s[i])-ord('0') 就是对应的整数。若此整数在 1-26之间，就是符合规则。

 再通过动态规划思想，判断 S 可能对应着多少种映射结果