[深度学习基础] 斯坦福CS231n李飞飞计算机视觉Lecture 6笔记

本文探讨了多种梯度下降优化算法，包括SGD、SGD+Momentum、Nesterov momentum、AdaGrad、RMSProp及Adam，并对比了它们的优劣。此外，还介绍了学习率衰减策略及一些二阶优化算法。针对过拟合问题，文章讨论了L1、L2正则化、最大范式约束、Dropout及数据扩充等正则化方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

内容列表

Lecture 6 Training Neural Networks，Part 2
小结

Lecture 6 Training Neural Networks，Part 2

多种梯度下降优化方式

SGD

本节讨论多种梯度下降的优化方式，之前我们着重讲了随机梯度下降SGD方式，这是一种很容易理解的梯度下降方式，但是，其实SGD方式在某些特定情况会很慢，比如，当数据处于下图这种椭圆形式的梯度时，SGD可能沿浅维度进展非常缓慢，并且沿陡峭方向抖动，虽然下降到了极小值点，但是速度极慢：
在这里插入图片描述
还有其他两种情况，SGD都到不了全局极小值点，比如当SGD运行到局部极小值点与鞍点时，梯度下降为0，SGD被卡住，并且其实在多维数据中，鞍点情况极为常见，这里说一下局部极小值点，在越来越多的研究表明，当你的规模越大时，局部极小值与全局极小值会越来越接近，这也是一个对模型设计有益现象：
在这里插入图片描述

SGD + Momentum

动量（Momentum）更新是另一个方法，这个方法在深度网络上几乎总能得到更好的收敛速度。该方法可以看成是从物理角度上对于最优化问题得到的启发。损失值可以理解为是山的高度（因此高度势能是 $U = m g h$ ，所以有 $U\propto h$ ）。用随机数字初始化参数等同于在某个位置给质点设定初始速度为0。这样最优化过程可以看做是模拟参数向量（即质点）在地形上滚动的过程。因为作用于质点的力与梯度的潜在能量（ $F=-\nabla U$ ）有关，质点所受的力就是损失函数的（负）梯度。还有，因为 $F = m a$ ，所以在这个观点下（负）梯度与质点的加速度是成比例的。

注意这个理解和上面的随机梯度下降（SGD）是不同的，在普通版本中，梯度直接影响位置。而在这个版本的更新中，物理观点建议梯度只是影响速度，然后速度再影响位置：
在这里插入图片描述
这里将速度初始化为0，还有一个参数rho，这个参数在最优化的过程中被看做动量（一般值设为0.9），但其物理意义与摩擦系数更一致。这个变量有效地抑制了速度，降低了系统的动能，不然质点在山底永远不会停下来。通过交叉验证，这个参数通常设为[0.5,0.9,0.95,0.99]中的一个。这个动量也可以随时间慢慢变化改善效果，一个典型的设置是刚开始将动量设为0.5而在后面的多个周期（epoch）中慢慢提升到0.99。

还有另一种解释方法：在普通的梯度下降法 $x = x - V$ 中，每次 $x$ 的更新量 $V$ 为 $V = d x * λ$ ;

当使用动量时， $V$ 考虑为本次的梯度下降量与部分上次更新量的矢量和，即 $- d W * λ$ 与上次 $x$ 的更新量 $V$ 乘以一个介于[0, 1]的系数momemtum的和，即: $V = d W * λ + V * m o m e m t u m$

从而使得动量方法有以下两条性质：

当本次梯度下降方向与上次更新量的方向相同时，上次的更新量能够对本次的搜索起到一个正向加速的作用。
当本次梯度下降方向与上次更新量的方向相反时，上次的更新量能够对本次的搜索起到一个减速的作用。

这个理解方法个人觉得更好一些。

Nesterov momentum

Nesterov动量与普通动量有些许不同，最近变得比较流行。在理论上对于凸函数它能得到更好的收敛，在实践中也确实比标准动量表现更好一些。

Nesterov动量的核心思路是，当参数向量位于某个位置x时，观察上面的动量更新公式可以发现，动量部分（忽视带梯度的第二个部分）会通过 $\rho * v$ 稍微改变参数向量。因此，如果要计算梯度，那么可以将未来的近似位置 $\rho * v$ 看做是“向前看”，这个点在我们一会儿要停止的位置附近。因此，计算 $\rho * v$ 的梯度而不是“旧”位置x的梯度就有意义了。
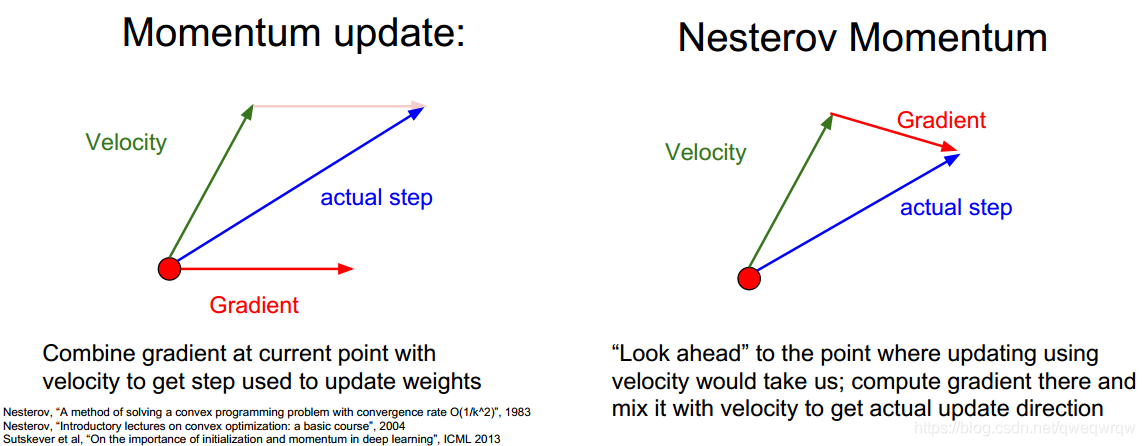
在这里插入图片描述
注意上图左边，将实际方向看作是初始梯度向量与动量向量的和，“向前看”意味着直接在动量向量结尾处直接计算梯度向量：

上图中上面方块中的等式（原始梯度计算等式）通过中间的等式可以转换为下面方块中的等式（动量向量结尾处的梯度计算等式），也就是新的梯度计算方法，下面是代码表示：
在这里插入图片描述

AdaGrad

此方法是一种自适应性学习率算法，下面是它的代码：

grad_squared = 0
while True:
	dx = compute_gradient(x)
	grad_squared += dx * dx
	x -= lraening_rate * dx / (np.sqrt(grad_squared) + 1e-7)

注意，此方法跟踪了每个参数的梯度的平方和。归一化是逐元素进行的。值得参考的是，接收到高梯度值的权重更新的效果被减弱，而接收到低梯度值的权重的更新效果将会增强。有趣的是平方根的操作非常重要，如果去掉，算法的表现将会糟糕很多。用于平滑的式子 $e p s$ （一般设为 $1 e - 4$ 到 $1 e - 8$ 之间）是防止出现除以0的情况。Adagrad的一个缺点是，在深度学习中单调的学习率被证明通常过于激进且过早停止学习。

RMSProp

RMSProp方法就是在AdaGrad方法上的改进，此方法让AdaGrad方法不再那么激进，可以单调的降低学习率，因为它使用了一个梯度平方的滑动平均：
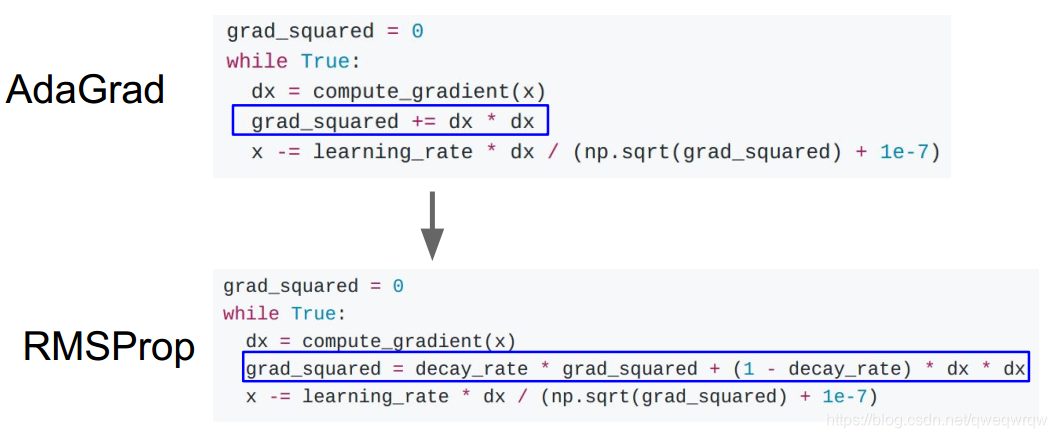
在这里插入图片描述
在上面的代码中，decay_rate是一个超参数，常用的值是[0.9,0.99,0.999]。剩下和AdaGrad完全一样，因此，RMSProp仍然是基于梯度的大小来对每个权重的学习率进行修改，这同样效果不错。但是和Adagrad不同，其更新不会让学习率单调变小。

Adam

可以看到上面几种方法中，Momentum与Nesterov momentum方法是结合动量，AdaGrad与RMSProp是通过类似于学习率的衰减，那么将他们结合会不会有更好的效果呢？这就是Adam算法：
在这里插入图片描述
上图中first_moment是运用动量特性，second_moment结合学习率衰减特性，二者结合后比以往的单独方法要效果更好，一般beta1设置为0.9，beta2设置为0.999，学习率一般1e-3或5e-4为最好模型；注意上面是这个方法的简单代码，而完整代码会将first_moment与second_moment增加一个偏执，使其不会在初始为0处失去效果：
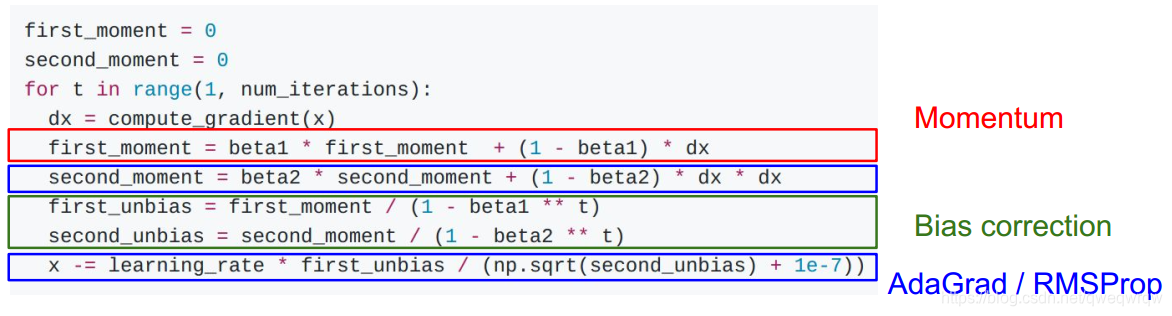
在这里插入图片描述
在实际操作中，推荐使用Adam作为默认的算法，一般而言跑起来比其他的算法都要好。

学习率衰减

在训练深度网络的时候，让学习率随着时间衰减通常是有帮助的。可以这样理解：如果学习率很高，系统的动能就过大，参数向量就会无规律地跳动，不能够稳定到损失函数更深更窄的部分去。知道什么时候开始衰减学习率是有技巧的：慢慢减小它，可能在很长时间内只能是浪费计算资源地看着它混沌地跳动，实际进展很少。但如果快速地减少它，系统可能过快地失去能量，不能到达原本可以到达的最好位置。通常，实现学习率衰减有3种方式：

随步数衰减：每进行几个周期就根据一些因素降低学习率。典型的值是每过5个周期就将学习率减少一半，或者每20个周期减少到之前的0.1。这些数值的设定是严重依赖具体问题和模型的选择的。在实践中可能看见这么一种经验做法：使用一个固定的学习率来进行训练的同时观察验证集错误率，每当验证集错误率停止下降，就乘以一个常数（比如0.5）来降低学习率。
指数衰减。数学公式是 $\alpha=\alpha_0e^{-kt}$ ，其中 $\alpha_0,k$ 是超参数， $t$ 是迭代次数（也可以使用周期作为单位）。
1/t衰减的数学公式是 $\alpha=\alpha_0/(1+kt)$ ，其中 $\alpha_0,k$ 是超参数， $t$ 是迭代次数。

在实践中，我们发现随步数衰减的随机失活（dropout）更受欢迎，因为它使用的超参数（衰减系数和以周期为时间单位的步数）比k更有解释性。最后，如果你有足够的计算资源，可以让衰减更加缓慢一些，让训练时间更长些，而且在进行其他梯度下降法时，也结合着学习率衰减也是很不错的选择。

一些二阶算法(L-BFGS)

在深度网络背景下，第二类常用的最优化方法是基于牛顿法的，其迭代如下：
$\displaystyle x\leftarrow x-[Hf(x)]^{-1}\nabla f(x)$
这里 $H f (x)$ 是Hessian矩阵，它是函数的二阶偏导数的平方矩阵。 $\nabla f(x)$ 是梯度向量，这和梯度下降中一样。直观理解上，Hessian矩阵描述了损失函数的局部曲率，从而使得可以进行更高效的参数更新。具体来说，就是乘以Hessian转置矩阵可以让最优化过程在曲率小的时候大步前进，在曲率大的时候小步前进。需要重点注意的是，在这个公式中是没有学习率这个超参数的，这相较于一阶方法是一个巨大的优势。

然而上述更新方法很难运用到实际的深度学习应用中去，这是因为计算（以及求逆）Hessian矩阵操作非常耗费时间和空间。举例来说，假设一个有一百万个参数的神经网络，其Hessian矩阵大小就是[1,000,000 x 1,000,000]，将占用将近3,725GB的内存。这样，各种各样的拟-牛顿法就被发明出来用于近似转置Hessian矩阵。在这些方法中最流行的是L-BFGS，该方法使用随时间的梯度中的信息来隐式地近似（也就是说整个矩阵是从来没有被计算的）。

然而，即使解决了存储空间的问题，L-BFGS应用的一个巨大劣势是需要对整个训练集进行计算，而整个训练集一般包含几百万的样本。和小批量随机梯度下降（mini-batch SGD）不同，让L-BFGS在小批量上运行起来是很需要技巧，同时也是研究热点。

几种方法的比较

以上两张gif可以很直观的看出几种方法的更新速度与更新方式。

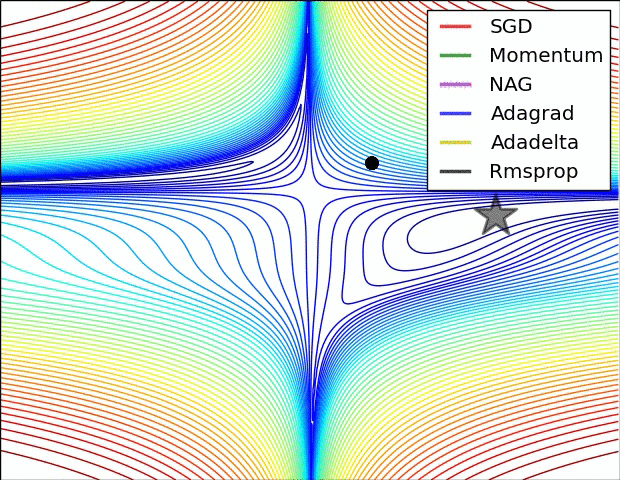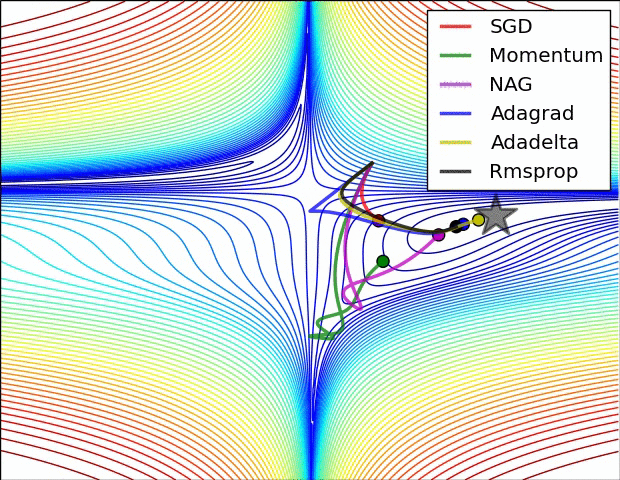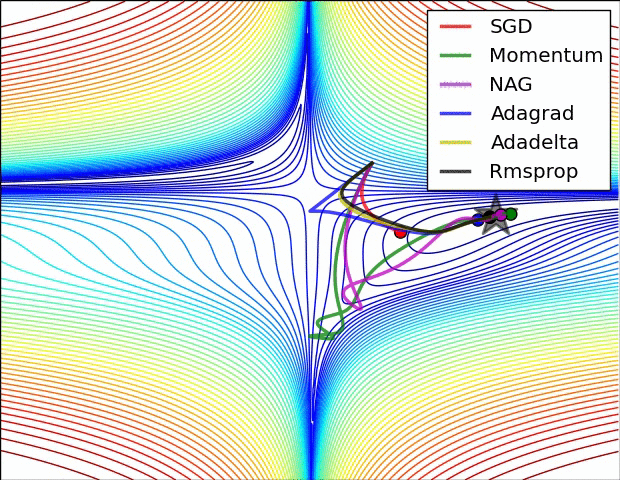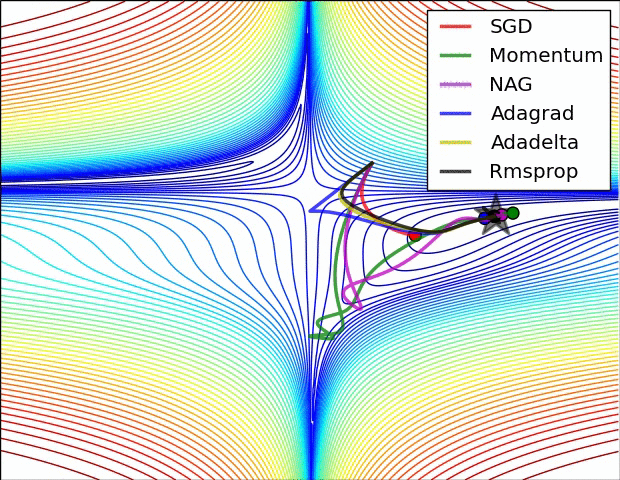
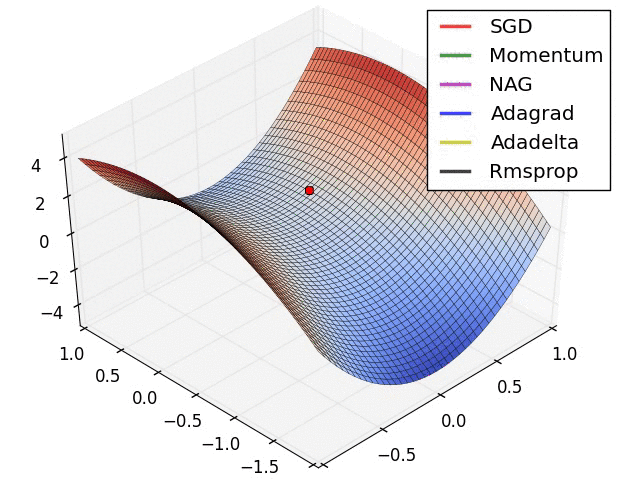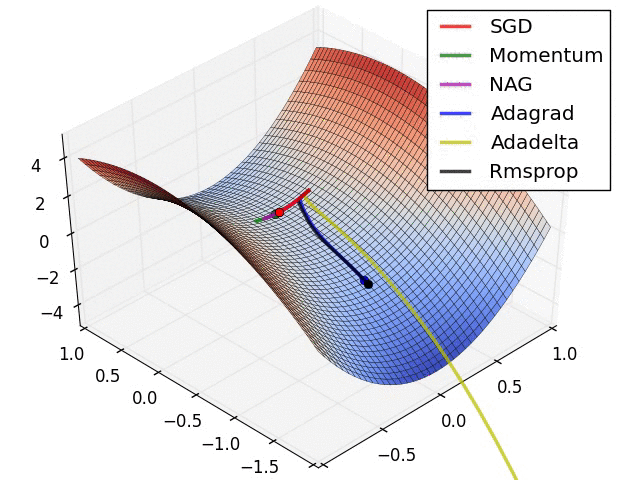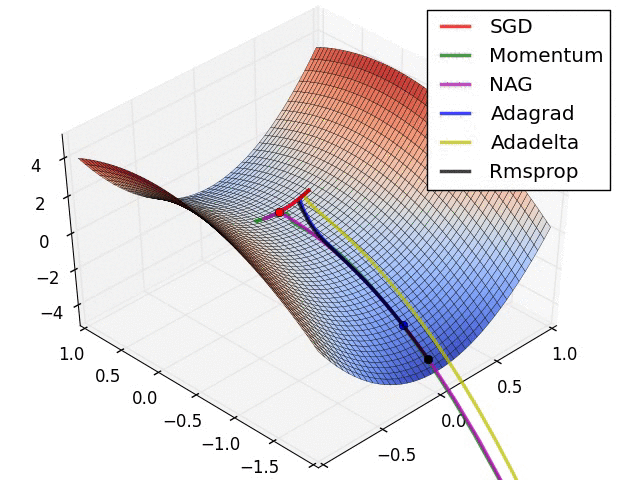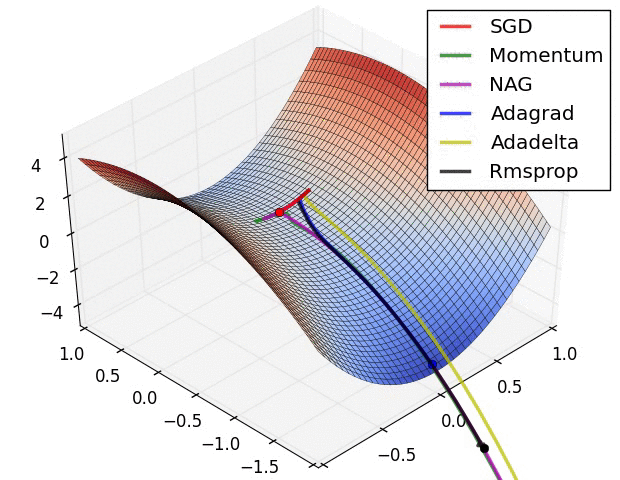
正则化

之前讲过的正则化意思是通过对权重参数的抑制使其不会过度学习，其实正则化的目的就是减少训练误差，有不少方法是通过控制神经网络的容量来防止其过拟合的，在训练数据不够多时，或者overtraining时，常常会导致overfitting（过拟合）。随着训练过程的进行，模型复杂度增加，在训练集上的error渐渐减小，但是在验证集上的error却反而渐渐增大——因为训练出来的网络过拟合了训练集，对训练集外的数据却不work，这里说一下，正则化一般是在验证数据集中体现出来的，并且从验证数据集的表现来影响训练数据集。

L2正则化

L2正则化可能是最常用的正则化方法了。可以通过惩罚目标函数中所有参数的平方将其实现。即对于网络中的每个权重 $w$ ，向目标函数中增加一个 $\frac{1}{2}\lambda w^2$ ，其中 $\lambda$ 是正则化强度。前面这个 $\frac{1}{2}$ 很常见，是因为加上 $\frac{1}{2}$ 后，该式子关于 $w$ 梯度(导数)就是 $\lambda w$ 而不是 $2\lambda w$ 了。L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚，倾向于更加分散的权重向量。在Lecture 3中讨论过，由于输入和权重之间的乘法操作，这样就有了一个优良的特性：使网络更倾向于使用所有输入特征，而不是严重依赖输入特征中某些小部分特征。最后需要注意在梯度下降和参数更新的时候，使用L2正则化意味着所有的权重都以 $-\lambda w$ 向着0线性下降。

L1正则化

L1正则化是另一个相对常用的正则化方法。对于每个 $w$ 我们都向目标函数增加一个 $\lambda|w|$ 。L1和L2正则化也可以进行组合： $\lambda_1|w|+\lambda_2w^2$ ，这也被称作Elastic net regularizaton。L1正则化有一个有趣的性质，它会让权重向量在最优化的过程中变得稀疏（即非常接近0）。也就是说，使用L1正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集，同时对于噪音输入则几乎是不变的了。相较L1正则化，L2正则化中的权重向量大多是分散的小数字。在实践中，如果不是特别关注某些明确的特征选择，一般说来L2正则化都会比L1正则化效果好。

最大范式约束

最大范式约束（Max norm constraints）。另一种形式的正则化是给每个神经元中权重向量的量级设定上限，并使用投影梯度下降来确保这一约束。在实践中，与之对应的是参数更新方式不变，然后要求神经元中的权重向量 $\overrightarrow{w}$ 必须满足 $||\overrightarrow{w}||_2<c$ 这一条件，一般 $c$ 值为3或者4。有研究者发文称在使用这种正则化方法时效果更好。这种正则化还有一个良好的性质，即使在学习率设置过高的时候，网络中也不会出现数值“爆炸”，这是因为它的参数更新始终是被限制着的。

Dropout

随机失活（Dropout）是一个简单又极其有效的正则化方法。该方法与L1正则化，L2正则化和最大范式约束等方法互为补充。在训练的时候，随机失活的实现方法是让神经元以超参数p的概率被激活或者被设置为0，一般来说，p值会被设置为0.5。
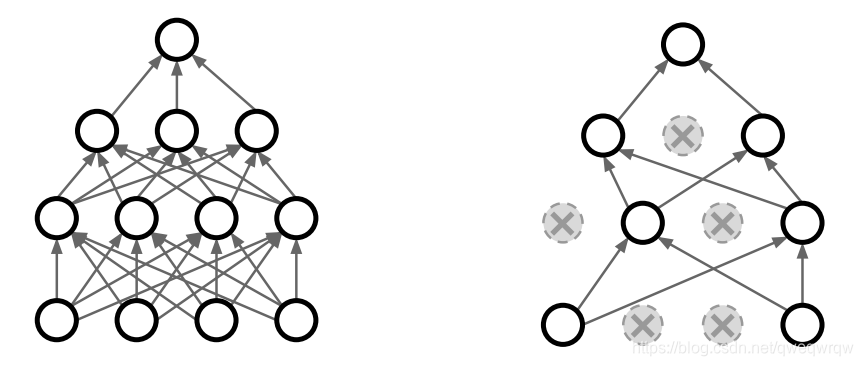
在这里插入图片描述
训练时的网络如图所示，在每一次前向与后向传播中都使用一半的子网络来训练可以大大的提高网络的表现情况，这是为什么呢？从下面的表示方法可以了解到这个理论的具体过程：

如上图所示，每一次在学习过程中防止几项功能的共同适应，而强制使网络有几项冗余特征是很好的消除过拟合的方式，其实在学习的过程中，失活的神经元参数是不会被前向与后向传播更新的，只有被激活的才会更新，就相当于在使用一个数据来训练大网络中的一个子网络，也就是说在多次循环中使用相同的数据点来训练不同的有共有参数的模型。

所以，整体来说，在训练过程中，随机失活可以被认为是对完整的神经网络抽样出一些子集，每次基于输入数据只更新子网络的参数（然而，数量巨大的子网络们并不是相互独立的，因为它们都共享参数）。

在测试过程中不使用随机失活，可以理解为是对数量巨大的子网络们做了模型集成（model ensemble），以此来计算出一个平均的预测。
在这里插入图片描述
可以看到训练过程中的期望是测试的期望的 $\frac{1}{2}$ ，所以，在测试时，可以将测试的过程中参数乘以 $\frac{1}{2}$ 。

数据扩充

数据扩充（Data Augmentation）也是一种常见的正则化方式，它的意义就在于，数据量更多，那么训练出的模型就会更好，可是往往我们的训练数据就那么些，怎么扩充呢？其实可以在原数据上进行改动，做一些变换，达到扩充数据的效果：

图像翻转
图像旋转
图像增亮
添加随机噪声
截取图像的部分
对图像进行弹性畸变

以上就是正则化的大致操作，其实上一节的批量归一化（Batch Normalization）也是一种正则化方式，其实还有更多方法，这里就不一一赘述了，可以上网寻找~~

小结

讨论几类梯度下降算法，最后推荐在大多数情况下使用Adam算法，或者使用SGD+Momentum算法并且结合学习率衰减的方法。其实当数据量较小时，也可以使用二阶L-BFGS算法。
讨论几类减小训练误差的正则化方式，有通过控制权重的L1、L2正则化，通过随机失活的Dropout，扩充数据集，还有Batch Normalization的方式，来尽量使验证集的准确率提升，训练出更好的模型。

资料来源：