[leetcode] Python(33)--验证二叉搜索树(98)、将有序数组转换为二叉搜索树(108)、删除链表中的节点(237)、合并两个有序数组(88)

从零开始的力扣（第三十三天）~

1. 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

示例 2:

—————————————————————————————————————————

最开始想法是递归左子树与右子树，但是这样不能包括根节点的数值，可能出现特殊情况，最后想到用中序遍历解决，因为二叉搜索树的中序遍历必须是由小到大并且无重复的

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        ans = []
        def DFS(root):
            if not root:
                return
            DFS(root.left)
            ans.append(root.val)
            DFS(root.right)
        DFS(root)
        if sorted(ans) == ans and len(ans) == len(set(ans)):
            return True
        return False

2.将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

—————————————————————————————————————————

先考虑特殊情况，nums长度为0，1，2时候如何判定，再递归判定nums更长的情况，并且分为奇偶两种情况

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if not nums:
            return
        if len(nums) == 1:
            node = TreeNode(nums[0])
            return node
        if len(nums) == 2:
            node1 = TreeNode(nums[0])
            node2 = TreeNode(nums[1])
            node2.left = node1
            return node2
        if len(nums) % 2 == 0:
            mid = len(nums) // 2 - 1
            root = TreeNode(nums[mid])
            root.left = self.sortedArrayToBST(nums[:mid])
            root.right = self.sortedArrayToBST(nums[mid + 1:])
            return root
        else:
            mid = (len(nums) - 1) // 2
            root = TreeNode(nums[mid])
            root.left = self.sortedArrayToBST(nums[:mid])
            root.right = self.sortedArrayToBST(nums[mid + 1:])
            return root

3.删除链表中的节点

请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点，你将只被给定要求被删除的节点。

现有一个链表 – head = [4,5,1,9]，它可以表示为:

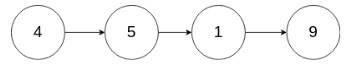
示例 1:
输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

示例 2:
输入: head = [4,5,1,9], node = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.

说明:
链表至少包含两个节点。
链表中所有节点的值都是唯一的。
给定的节点为非末尾节点并且一定是链表中的一个有效节点。
不要从你的函数中返回任何结果。
—————————————————————————————————————————

和一般的删除节点不同，这里给定的只有被删除节点，那么就可以根据被删除节点的属性来替换被删除节点，例如将后一个节点的属性替代本节点

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteNode(self, node):
        """
        :type node: ListNode
        :rtype: void Do not return anything, modify node in-place instead.
        """
        node.val, node.next= node.next.val, node.next.next

4.合并两个有序数组

给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。

说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。

示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3

输出: [1,2,2,3,5,6]
—————————————————————————————————————————

比较麻烦，遍历nums1的数，发现大于等于nums2的第一位时，插入元素，每次进行一下简单判断nums1最后一个元素是否小于nums2的第一个元素

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        k = 0
        while nums2:
            if nums1[m + k - 1] <= nums2[0]:
                nums1[m + k:m + k + n] = nums2
                nums2 = []
                break
            i = 0
            while nums1[i] < nums2[0]:
                i += 1
            nums1[i + 1:m + k + 1] = nums1[i:m + k]
            nums1[i] = nums2.pop(0)
            k += 1

另一种偷鸡的方法，将nums1后面元素替换成nums2，然后sort

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        nums1[m:m + n] = nums2
        nums1.sort()

以上就是今日经验！