机器学习实战（六）决策树（上）

前言：
决策树（Decision Tree）是一种基本的分类与回归方法，本文主要讨论分类决策树。 决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。相比朴素贝叶斯分类，决策树的优势在于构造过程不需要任何领域知识或参数设置，因此在实际应用中，对于探测式的知识发现，决策树更加适用。

一、从分类问题开始

分类（Classification）任务就是确定对象属于哪个预定义的目标类。 分类问题不仅是一个普遍存在的问题，而且是其他更加复杂的决策问题的基础，更是机器学习和数据挖掘技术中最庞大的一类算法家族。我们前面介绍过的很多算法（例如SVM，朴素贝叶斯等）都可以用来解决分类问题。作为本文的开始，我们首先来简单回顾一下什么是分类。

假设我们现在有如下表所示的一个属性集（feature set），它收集了几个病患的症状和对应的病症。症状包括头疼的程度、咳嗽的程度、体温以及咽喉是否肿痛，这些症状（feature）的组合就对应一个病症的分类（Cold 还是 Flu）。

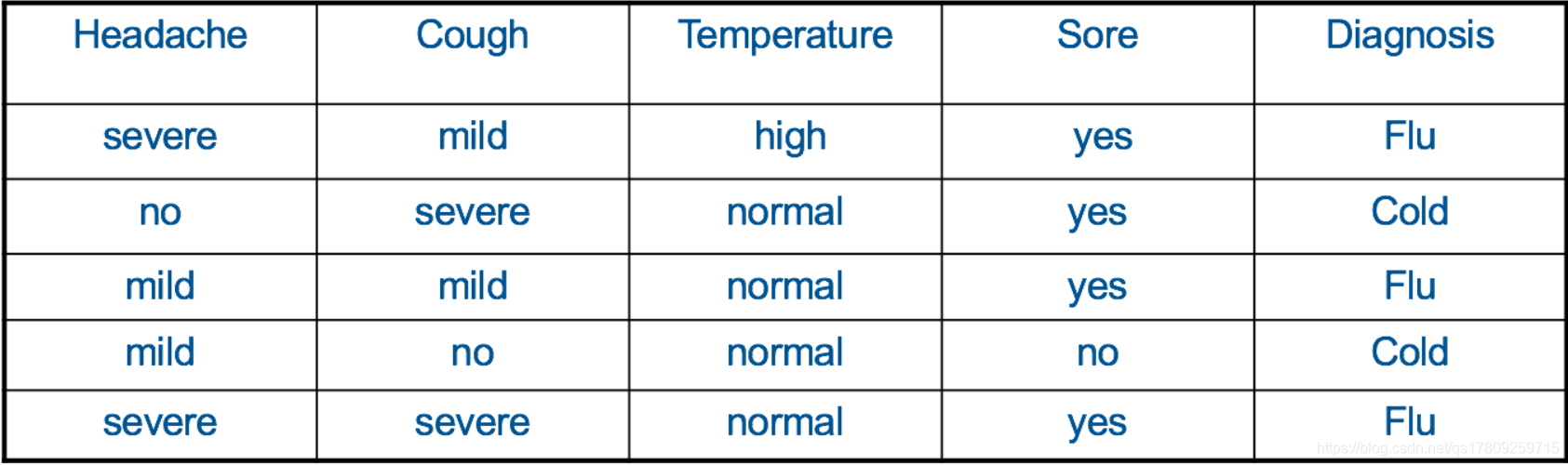
分类问题的本质就是当给定这样一个数据集后，要求我们训练出（或建立）一个模型ff。当出现一组新的特征向量时，要求我们预测（或判断）拥有这样一组特征向量的对象应当属于哪个类别。就我们现在给出的例子而言，假设你是一名医生，现在收治了一位新的病患，然后你通过问诊得知他的一些症状（包括头疼的程度、咳嗽的程度、体温以及咽喉是否肿痛），然后你就要根据你已经建立好的模型来判断该病人得的到底是Cold（普通感冒）还是Flu（流行性感冒）。

分类问题的类别数目可以是两类也可以是多类。二分类问题是最简单的分类问题，而多分类问题模型可以在二分类模型的基础上进行构建。我们在前面文章中一直使用的鸢尾花数据集就是一个典型的多分类问题，问题的最终目标是判断给定一朵花，它应该属于setosa、versicolor和virginica中的哪一类。

二、决策树模型

1.概念
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部节点和叶节点，内部节点表示一个特征或属性，叶节点表示一个类。
分类的时候，从根节点开始，对实例的某一个特征进行测试，根据测试结果，将实例分配到其子结点；此时，每一个子结点对应着该特征的一个取值。如此递归向下移动，直至达到叶结点，最后将实例分配到叶结点的类中。

2.举一个通俗的栗子
决策树可以理解成是很多if−then的规则组合.由决策树的根结点到叶结点的每一条路径构建一条规则；路径上的内部结点的特征对应着规则的条件，而叶结点对应着分类的结论。决策树的路径和其对应的if-then规则集合是等效的，它们具有一个重要的性质：互斥并且完备。这里的意思是说：每一个实例都被一条路径或一条规则所覆盖，而且只被一条规则所覆盖。
下图就是一棵典型的决策树:

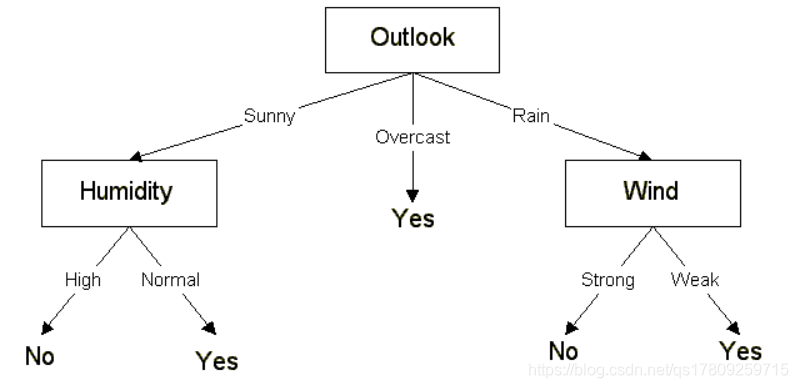
这棵决策树根据天气情况分类“星期六上午是否适合打网球”,根节点到叶节点的每一条路径构成了一条规则,路径上的内部节点对应规则的条件,叶节点的类对应着规则的结论.

规则1:如果晴天,湿度很高就不去打网球
规则2:如果晴天,湿度一般就去打网球
规则3:如果是阴天,就去打网球