算法学习2-二分和前缀和简单总结

一、二分

基本思想：二分是一种高效的查询算法思想，核心是在于不断缩小区间来查找目标值的过程。

• 首先要确定区间，假设数组长度为n，则数组的区间范围可能是a[0,1,2,……n-1]
• 其次要找一个具有二段性的性质。即可能前半段满足这个性质而后半段不满足这个性质。
  具体例子而言：在一个有序数组[1, 3, 5, 7, 9, 11, 13]中查找数字7。我们可以定义这样一个性质：数组中某个位置i的元素小于等于7。那么对于这个数组，从起始位置到7所在位置（包含7）的元素都满足该性质，而7之后的元素都不满足。即[1, 3, 5, 7]满足性质，[9, 11, 13]不满足性质。

具体情况：
当查找最小值的时候：如果check(mid)满足条件，说明mid小于最小值，则需要mid=l+r+1>>1，这里+1是为了避免死循环问题。假设数组长度为2，如果不加1则l+r>>2=1则陷入死循环。

while(l<r):
	int mid = l+r+1>>1;
	if (check(mid)) l=mid;
	else:
		r=mid-1;
	

当求满足条件最大值的时候,r=mid；

	while(l < r)
	{
		int mid = l + r >> 1;
		if(check(mid)) r = mid;
		else l = mid + 1;
	}

二、前缀和

基本思想：前缀和是一种非常重要的预处理思想。其核心目的是降低算法的时间复杂度。特别是在处理区间查询问题时，可以显著降低查询的时间开销。通过提前计算并存储一些特定的值，在后续查询中可以直接利用这些值，避免重复计算，从而提高算法效率。
一维前缀和：
对于给定的数列我们定义：

• S₀=0
• S₁=a₁
• S₂=a₁+a₂
• S₃=a₁+a₂+a₃
• ……
• S_n=a₁+a₂+a₃+……+a_n
  可以用递推公式表示为
  $$Si=\sum _{i=1}^{n}ai-1+an$$
  假如我们要计算区间[L,R]中所有元素的和，一种常见的方式是依次从a_L遍历到a_R，时间复杂度为O(R-L+1)

a=[1,2,3,4,5,6]
L,R=1,3
sum_value=0
for i in range(L-1,R):
	sum_value+=a[i]
print(sum_value)

但是使用前缀和，我们可以使用S_R-S_L-1来进行计算，而其时间复杂度为O(1)

a=[1,2,3,4,5,6]
L,R=1,3
sum_value=0
n=len(a)
S = [0]*（n+1）
for i in range(1,n+1):
	S[i]=S[i-1]+a[i-1]
sum_value = S[R]-S[R-1]
print(sum_value)

使用前缀和计算区间和的时间复杂度为O(1)，因为只涉及到两次数组元素的访问和一次减法运算，大大提高了查询效率。
二维前缀和:
二维前缀和是一维前缀和在二维空间上的扩展，同样用于优化二维数组中矩形区域元素和的查询。
二维前缀和的定义与计算方法:
对于一个 m*n的二维数组a_ij(1<=i<=m,1<=j<=n)，我们定义其二维前缀和数组 S_ij表示从(1,1)到 (m,n)这个矩形区域内所有元素的和。
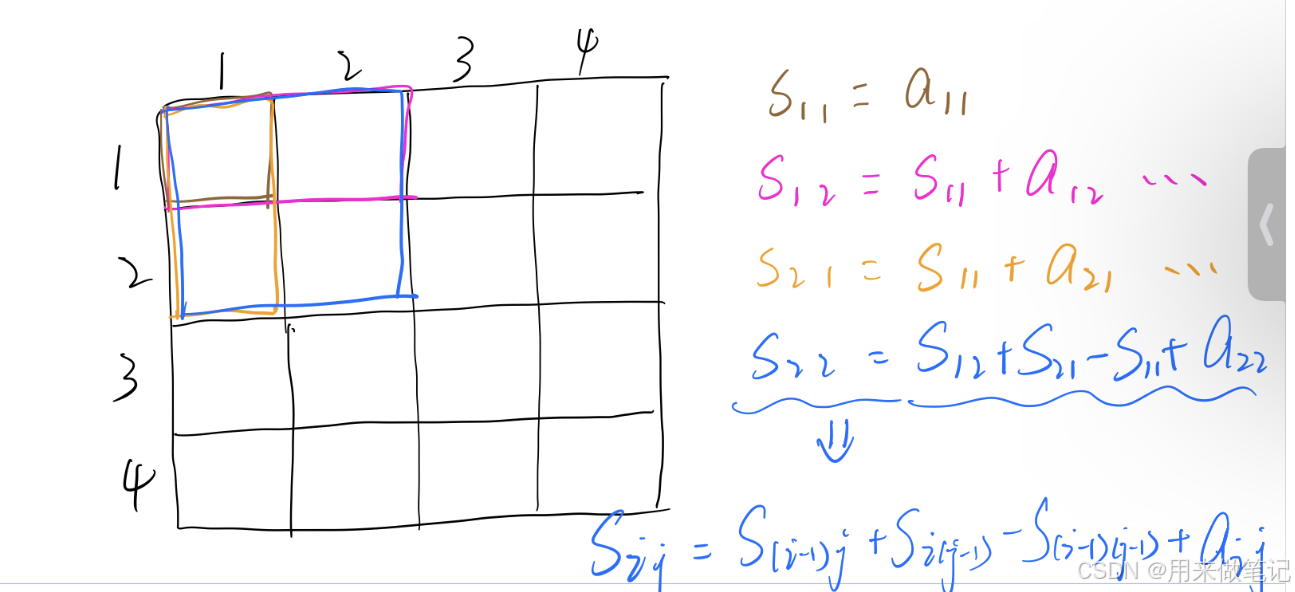
二维前缀和的递推公式为 S_ij= S_(i-1)j+ S_i(j-1) -S_(i-1)(j-1)+a_ij。下面解释这个公式的原理：

• S~(i-1)j表示第 1 行到第 i-1 行，第 1列到第 j 列这个矩形区域的元素和。
• S~(i-1)j表示第 1 行到第 i行，第 1 列到第 j -1 列这个矩形区域的元素和。
• 当我们把 S_(i-1)j 和 S_(i-1)j 相加时，会发现从（1，1）到 （i-1,j-1) 这个矩形区域的元素和被重复计算了一次，所以需要减去 。
• 最后再加上当前位置的元素 a_ij，就得到了从 (1,1)到 (i，j)这个矩形区域的元素和 S_(i-1)j。
  

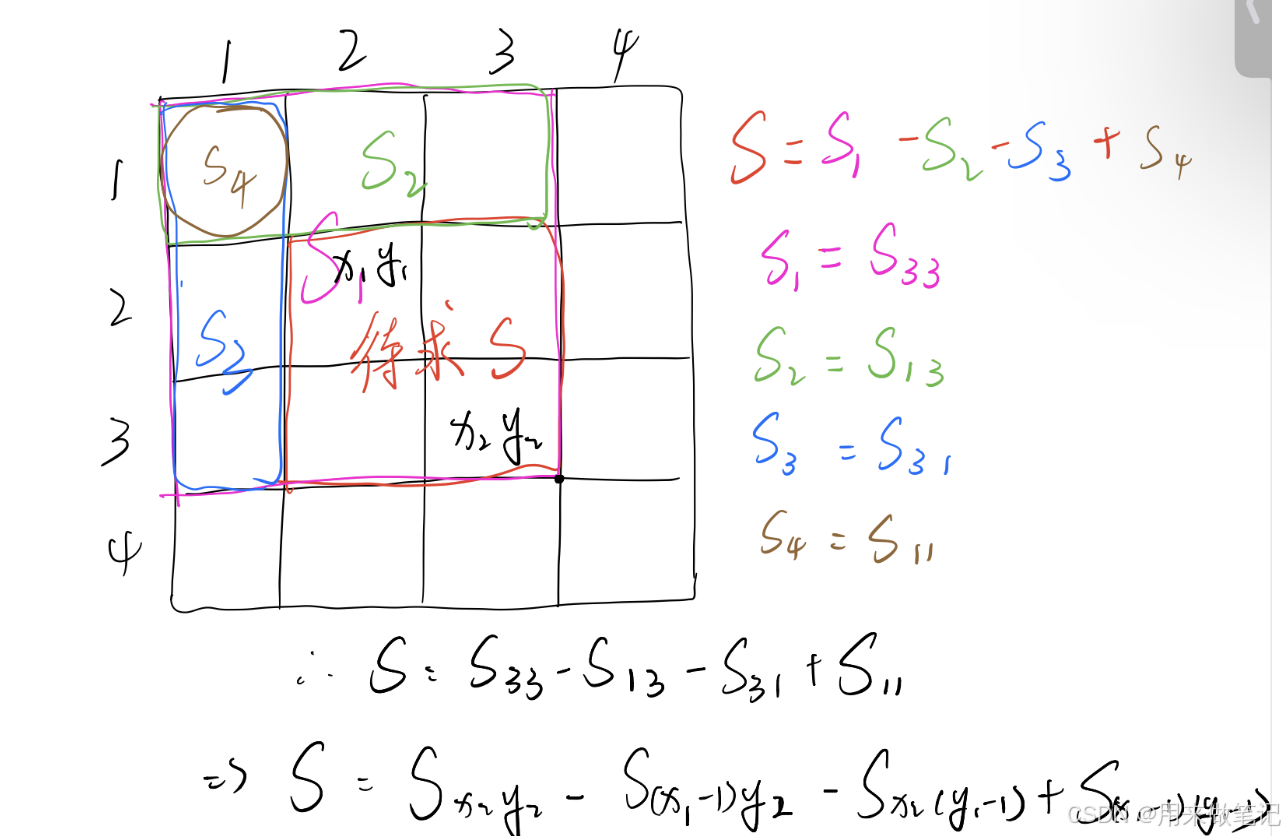
利用二维前缀和求矩形区域和：

如果我们需要计算二维数组中以（x₁，y₁)为左上角，（x₂，y₂)为右下角的矩形区域内所有元素的和，可以通过公式Sx2y2-S(x1-1)y2-Sx2(y1-1)+S(x1-1)(y1-1)来计算。原理和计算S_ij类似，通过对不同区域的前缀和进行加减运算，避免重复计算，从而将查询矩形区域和的时间复杂度从O(（x2-x1+1)(y2-y1+1))降低到O(1)

代码示例如下：

# 二维数组
a = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]
m, n = len(a), len(a[0])
# 初始化二维前缀和数组
S = [[0] * (n + 1) for _ in range(m + 1)]
# 计算二维前缀和
for i in range(1, m + 1):
    for j in range(1, n + 1):
        S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i - 1][j - 1]
# 计算以 (1, 1) 为左上角，(2, 2) 为右下角的矩形区域和
x1, y1, x2, y2 = 1, 1, 2, 2
sum_value = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]
print(sum_value)

综上所述，前缀和思想通过预处理的方式，将原本需要重复计算的区间和或矩形区域和问题的时间复杂度进行了优化，在实际应用中具有重要的价值。