java成长日记（10）

最新推荐文章于 2025-05-24 10:42:46 发布

无存在感路人甲

最新推荐文章于 2025-05-24 10:42:46 发布

阅读量101

点赞数 1

文章标签： java

本文链接：https://blog.youkuaiyun.com/qq_74321854/article/details/134168489

版权

文章讲述了如何使用Java实现稀疏矩阵的快速转置，通过三元组顺序表存储非零元素，并详细解释了转置过程中行列交换和位置映射的过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

今天数据结构课又学了点新东西，课下花了点时间才搞懂这些知识点- -下面我就关于三元组、稀疏矩阵来实现稀疏矩阵的快速转置展开讨论：

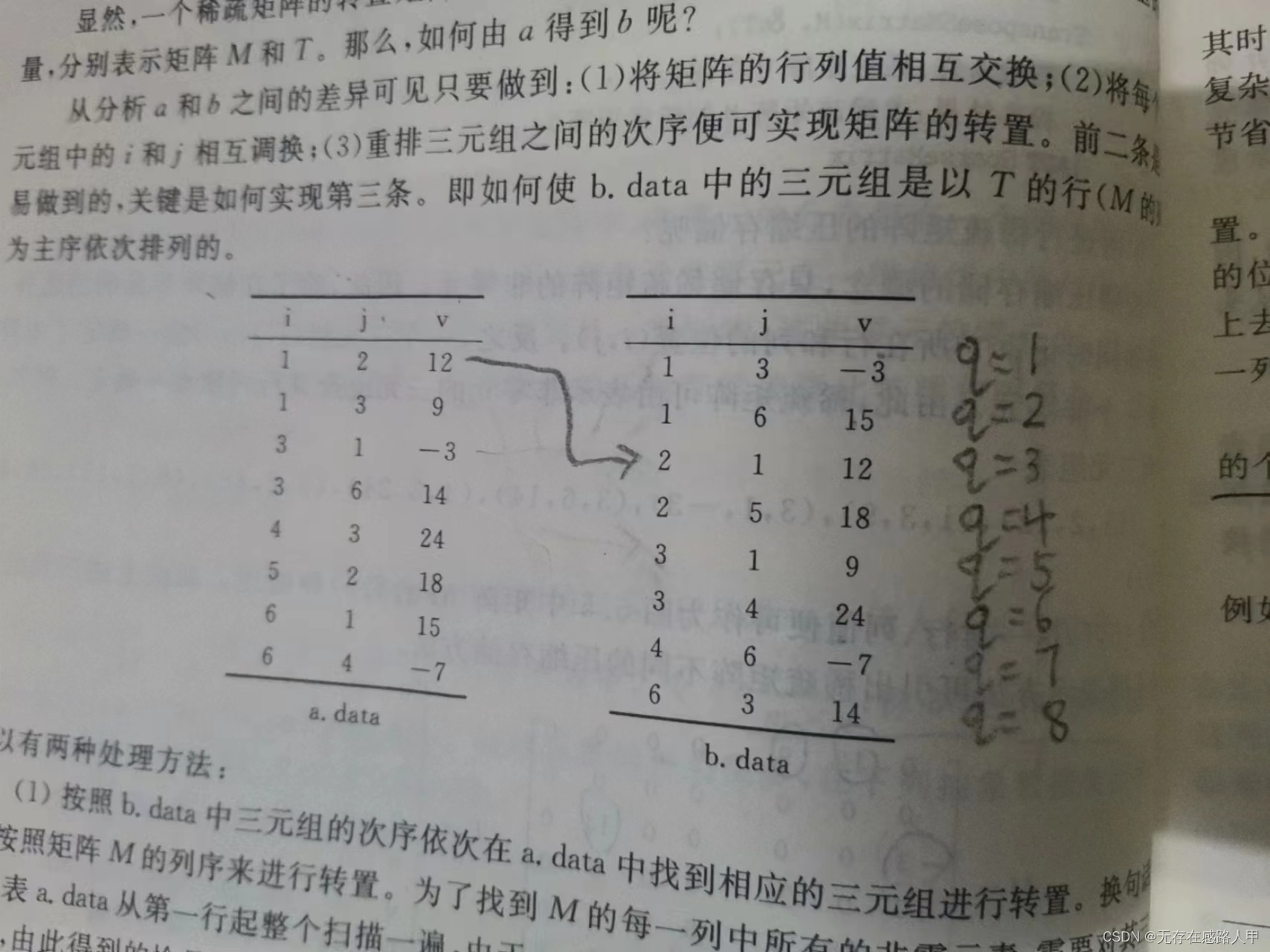
以我们数据结构课本的题目为例，现在我们有这样的一个矩阵

$\begin{bmatrix} &0 & 12 & 9& 0 & 0 & 0 &0\\ & 0 & 0& 0& 0 & 0& 0&0\\ & -3& 0 &0 & 0 &0 &14 &0\\ & 0&0 & 24 & 0 &0 & 0 &0\\ & 0 & 18 & 0&0 & 0& 0&0\\ & 15 & 0&0 &7 &0 &0 &0 \end{bmatrix}$

转置之后的矩阵为：

$\begin{bmatrix} & 0& 0& -3& 0&0 &15\\ & 12& 0 &0 & 0 &18 &0\\ & 9& 0 & 0& 24&0 &0\\ & 0&0 &0 & 0 &0 &-7\\ & 0& 0&0 &0 & 0&0\\ & 0 & 0 & 14 & 0 &0 &0\\ & 0 &0 & 0& 0 &0 &0 \end{bmatrix}$

首先，我们要建立一个三元组顺序表，先建立一个Triple类：

public class Triple<T> {
    int row,col;  //该非零元的行下标和列下标
    T v; //v为其值
    public Triple(){}
    public Triple(int row,int col, T v){
        this.row = row;
        this.col = col;
        this.v = v;
    }
}

之后建立一个TSMatrix类，里面包括了一个打印矩阵的方法display()：

public class TSMatrix {
    final int MAXSIZE = 10;
    int mu,nu,tu;
    Triple<Integer> data[] = new Triple[MAXSIZE + 1];//Java不支持泛型数组
    public TSMatrix(int mu, int nu, int tu){
        this.mu = mu;  //行数
        this.nu = nu;  //列数
        this.tu = tu;  //非零元个数
        for(int i=1; i<=MAXSIZE; i++)
            data[i] = new Triple();
    }
    public void display(){
        int i,j,k,m,n,count = 0;
        for(i=1; i<=mu; i++){
            for(j=1; j<=nu; j++){
                for(k=1; k<=tu; k++){
                    if(i==data[k].row && j==data[k].col){
                        System.out.print(data[k].v + " ");
                        count = -1;
                        break;
                    }
                }
                if(count != -1)
                    System.out.print("0 ");
                count = 0;
            }
            System.out.println();
        }
    }
}

之后，创建主类，在主类里实现快速转置的方法：

public class Transfer {

    public static void main(String[] args) {
        int i,j,k,l;
        Scanner scan = new Scanner(System.in);
        System.out.println("请输入矩阵的行数，列数，非零元的个数：");
        int mu,nu,tu;
        mu = scan.nextInt();
        nu = scan.nextInt();
        tu = scan.nextInt();
        TSMatrix M = new TSMatrix(mu,nu,tu);
        TSMatrix T = new TSMatrix(nu,mu,tu);
        System.out.println("请输入矩阵的三元组：");
        for(i=1; i<=tu; i++){
            M.data[i].row = scan.nextInt();
            M.data[i].col = scan.nextInt();
            M.data[i].v = scan.nextInt();
        }
        System.out.println("您输入的矩阵为：");
        M.display();
        //增加两个向量
        int num[] = new int[nu+1];//M1中第col列中非零元的个数
        int col,row,t;
        for(col=1; col<=nu; col++){  //各列元素个数初始化
            num[col] = 0;
        }
        for(t=1; t<=tu; t++){  //记录各列元素个数
            num[M.data[t].col]++;
        }
        int cpot[] = new int[nu+1];//M中第col列的第一个非零元在T.data中的位置。
        cpot[1] = 1;
        for(col=2; col<=nu; col++){  //记录起始位置
            cpot[col] = cpot[col - 1] + num[col - 1];  //copt[col]指示M中第col列的第一个非零元在b.data中的恰当位置
        }
        int p,q;//实现转置
        for(p=1; p<=tu; p++){
            col = M.data[p].col;  //行列交换
            q = cpot[col];
            T.data[q].row = M.data[p].col;
            T.data[q].col = M.data[p].row;
            T.data[q].v = M.data[p].v;  //元素交换
            cpot[col]++;  //当该位置存放一个三元组之后，则起始位置需要+1
        }
        System.out.println("转置后的矩阵为：");
        T.display();

    }

}

先解释一下display()的运行原理吧，当i和j分别等于三元组里的行数和列数时，会输出这个行数和列数所对应的非零元素，并把标志数count设置为-1，并break出去；当其跳到j层循环时，count标志符会重新设置为0；若i和j不等于等于三元组里的行数或列数时，count会等于0，从而满足count != -1的条件，此时会输出零元素。

接下来，我来讲一下这个代码里面最难理解的转置部分，也就是这个部分的代码：

 int p,q;//实现转置
        for(p=1; p<=tu; p++){
            col = M.data[p].col;  //行列交换
            q = cpot[col];
            T.data[q].row = M.data[p].col;
            T.data[q].col = M.data[p].row;
            T.data[q].v = M.data[p].v;  //元素交换
            cpot[col]++;  //当该位置存放一个三元组之后，则起始位置需要+1
        }

首先是这一行（第一次循环为例）：

col = M.data[p].col;  //行列交换

这是先取出三元组中M.data[1]的对应的列数；

然后是这一行：

q = cpot[col];

这是用q取出M中第2列的第一个非零元在新的三元组中的恰当位置，即是：

然后是这一段代码：

            T.data[q].row = M.data[p].col;
            T.data[q].col = M.data[p].row;
            T.data[q].v = M.data[p].v;

这就是在新三元组中的对应位置保存倒置后的行、列和值，如下图：

之后是这一步：

cpot[col]++;

当该位置存放一个三元组之后，则起始位置需要+1；

如法炮制，在执行第二次循环时其运行过程可抽象成下图：

我们可以通过debug证实我们的猜想：

所以，它是按照原三元组的顺序，通过cpot[col]一一将转置后的行、列和值“映射”到新三元组的相关位置。综上，这种快速转置法是“以空间换时间”的一种方式，能有效地减少算法的时间复杂度。

以上的叙述仅限于本人对该模块知识的理解，并不完全准确；如果有我理解错误的地方，请各位多多包涵T_T

参考代码：

作者：Pickle

出处：Pickle - 博客园