【数学建模】数据拟合与插值技术全解析：从线性插值到Logistic模型实战

原创已于 2025-04-10 17:40:40 修改 · 1.5k 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#数学建模 #python #机器学习 #算法

于 2025-02-25 19:48:10 首次发布

数学建模专栏收录该内容

10 篇文章

订阅专栏

请添加图片描述

💕 个人主页： Puszy-优快云博客💕

🎉 欢迎关注：👍点赞 📣留言 😍收藏 💖 💖 💖 华丽的跌倒，胜过无谓的徘。 –– 《人民日报》

🌈🌈🌈往期精选内容：

💖熵权法原理深度解析与数学建模实战–基于2021全国大学学建模C题供应商评价
 💖基于PyTorch的MLP模型的MNIST手写数字识别的Python代码

💖一、引言

在科学研究和工程实践中，处理离散数据并挖掘其背后规律是一项至关重要的任务。插值和拟合作为两种关键的数据处理方法，能够帮助我们从有限的已知数据中获取更多有价值的信息，进而实现对未知数据的有效估计和分析。
本文将深入探讨插值和拟合的相关知识，详细介绍线性插值、三次样条插值、最近邻点插值、双线性插值、双三次插值等不同插值方法，以及二次多项式拟合和非线性拟合等拟合方案。通过具体的题目案例、清晰的解决思路、直观的结果展示和详细的代码实现，为读者提供全面且深入的学习指导，帮助大家更好地掌握这些方法的原理和应用。

📚二、插值（Interpolation）

定义：插值是在已知离散数据点之间构造一个连续函数，使其严格通过所有已知点，从而估算未知位置的数值。其核心目标是精确还原数据点间的局部特征。

🚀2.1、线性插值和三次样条插值

📘2.1.1、题目

题目:要求使用两种插值方法来计算给定数据点在 (x) 每改变 0.1 时的 (y) 值。数据点如下：
$\begin{array}{c|cccccccccc} x & 0 & 3 & 5 & 7 & 9 & 11 & 12 & 13 & 14 & 15 \\ \hline y & 0 & 1.2 & 1.7 & 2.0 & 2.1 & 2.0 & 1.8 & 1.2 & 1.0 & 1.6 \\ \end{array}$
需要使用的两种插值方法是：

分段线性插值：这种方法在每对相邻的数据点之间使用直线段进行插值。这意味着在两个已知点之间，(y) 值会线性地从第一个点的 (y) 值变化到第二个点的 (y) 值。
三次样条插值：这种方法使用三次多项式在每对相邻的数据点之间进行插值，以确保在每个数据点处，函数值和一阶导数都是连续的。三次样条插值通常能提供比线性插值更平滑的曲线。

📘2.1.2、解决思路

分段线性插值：
- 对于每个 (x) 值（从 0 到 15，步长为 0.1），找到它所在的两个相邻 (x) 数据点。
- 使用这两个点的 (y) 值和 (x) 值计算线性插值的 (y) 值。
三次样条插值：
- 构建一个三次多项式，使其通过每对相邻的数据点。
- 确保在每个数据点处，多项式的值和一阶导数都与相邻点相匹配。
- 对于每个 (x) 值（从 0 到 15，步长为 0.1），使用构建的多项式计算 (y) 值。

通过这些步骤，可以计算出 (x) 每改变 0.1 时的 (y) 值。

📈2.1.3、结果展示

结果展示

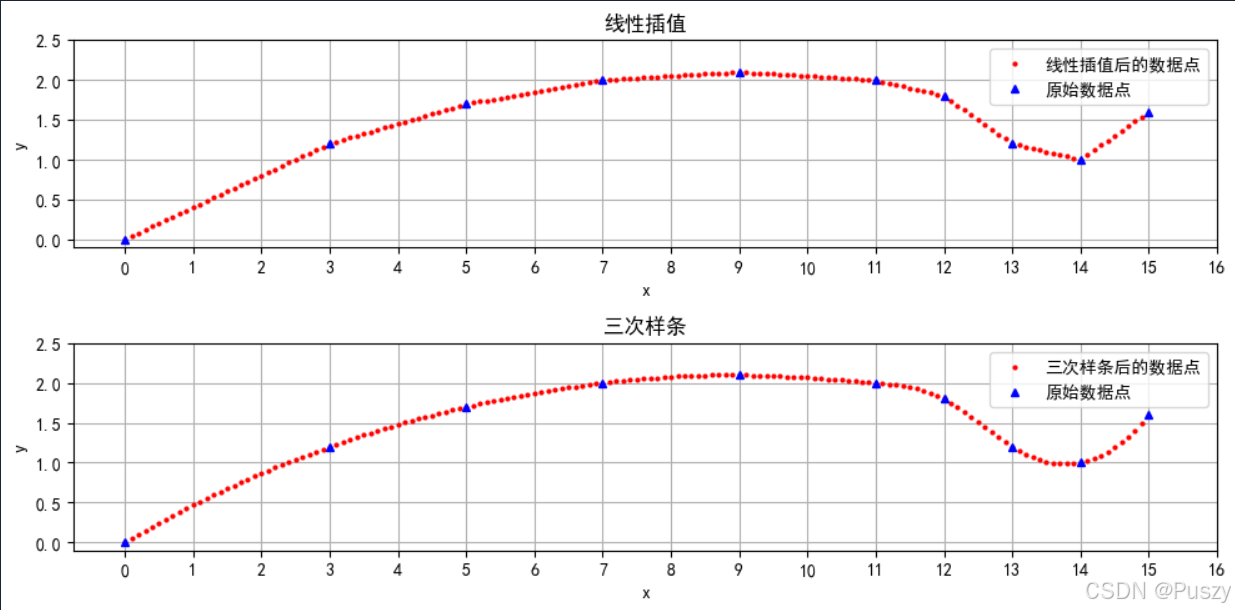
👉2.1.4、详细代码

# 导入必要的库
from matplotlib import font_manager  # 字体管理模块，用于中文字体显示
import numpy as np  # 数值计算库
import matplotlib.pyplot  as plt  # 绘图库
from scipy.interpolate  import interp1d  # 一维插值函数
import matplotlib  # 基础绘图库

# 设置全局字体（解决中文显示问题），设置加粗样式
matplotlib.rc("font",  family='SimHei', weight='bold')

# 定义原始数据点
x0 = [0, 3, 5, 7, 9, 11, 12, 13, 14, 15]  # 原始x坐标
y0 = [0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6]  # 原始y坐标

# 生成插值所需的密集x坐标（步长0.1）
x1 = np.arange(0,  15, 0.1)  # 创建从0到15的等差数列，间隔0.1

# 创建两种插值函数
f_linear = interp1d(x0, y0, kind='linear')  # 线性插值器
f_cubic = interp1d(x0, y0, kind='cubic')  # 三次样条插值器

# 生成插值后的y值
y1 = f_linear(x1)  # 线性插值结果
y2 = f_cubic(x1)   # 三次样条插值结果

# ------------------ 绘制线性插值子图 ------------------
plt.figure(figsize=(10,5),  dpi=100)  # 创建画布（宽10英寸，高5英寸，分辨率100）
plt.subplot(2,  1, 1)  # 创建2行1列的子图布局，定位第1个子图

# 绘制插值结果（红色圆点，大小4）和原始数据（蓝色三角，大小4）
plt.plot(x1,  y1, 'r.', markersize=4, label='线性插值后的数据点')
plt.plot(x0,  y0, 'b^', markersize=4, label='原始数据点')

# 设置坐标轴标签、网格、刻度范围和标题
plt.xlabel('x') 
plt.ylabel('y') 
plt.grid() 
plt.xticks(np.arange(0,17,1))   # x轴从0到16，步长1
plt.yticks(np.arange(0,3,0.5))   # y轴从0到2.5，步长0.5
plt.title(' 线性插值')
plt.legend()   # 显示图例

# ------------------ 绘制三次样条插值子图 ------------------
plt.subplot(2,  1, 2)  # 定位第2个子图
plt.plot(x1,  y2, 'r.', markersize=4, label='三次样条后的数据点')
plt.plot(x0,  y0, 'b^', markersize=4, label='原始数据点')

# 设置坐标轴标签、网格、刻度范围和标题（与第一个子图保持对称）
plt.xlabel('x') 
plt.ylabel('y') 
plt.grid() 
plt.xticks(np.arange(0,17,1)) 
plt.yticks(np.arange(0,3,0.5)) 
plt.title(' 三次样条')
plt.legend() 

# 自动调整子图间距，避免重叠
plt.tight_layout()

🚀2.2、最近邻点插值、双线性插值和双三次插值

📘2.2.1、题目

试作出该山区的地貌图和等高线图，并对最近邻点插值、双线性插值方法和双三次插值方法的插值效果进行比较。

y \ x	1200	1600	2000	2400	2800	3200	3600	4000
1200	1130	1250	1280	1230	1040	900	500	700
1600	1320	1450	1420	1400	1300	700	900	850
2000	1390	1500	1500	1400	900	1100	1060	950
2400	1500	1200	1100	1350	1450	1200	1150	1010
2800	1500	1200	1100	1550	1600	1550	1380	1070
3200	1500	1550	1600	1550	1600	1600	1600	1550
3600	1480	1500	1550	1510	1430	1300	1200	980

📘2.2.2、解决思路

根据要求，可以按照以下步骤来解决这个问题：

1. 数据准备
首先，使用 numpy 数组来存储这些数据，并使用 np.meshgrid 函数生成网格坐标。

2. 插值函数定义
定义一个名为 interpolate 的函数，该函数接受原始数据点的坐标和值，以及插值方法和插值点的数量。这个函数使用 scipy.interpolate.griddata 函数进行插值，生成插值后的网格数据。

3. 插值方法选择
选择三种插值方法：最近邻点插值（‘nearest’）、双线性插值（‘linear’）和双三次插值（‘cubic’）。这些方法用于比较插值效果。

4. 绘制3D地貌图和等高线图
使用 matplotlib 和 mpl_toolkits.mplot3d 绘制3D地貌图和等高线图。首先，绘制原始数据的3D图和等高线图。然后，对于每种插值方法，绘制插值后的3D图和等高线图。

5. 比较插值效果
通过比较不同插值方法生成的3D地貌图和等高线图，可以评估每种方法的效果。包括观察插值结果的平滑度、准确性和细节表现。

📈2.2.3、结果展示

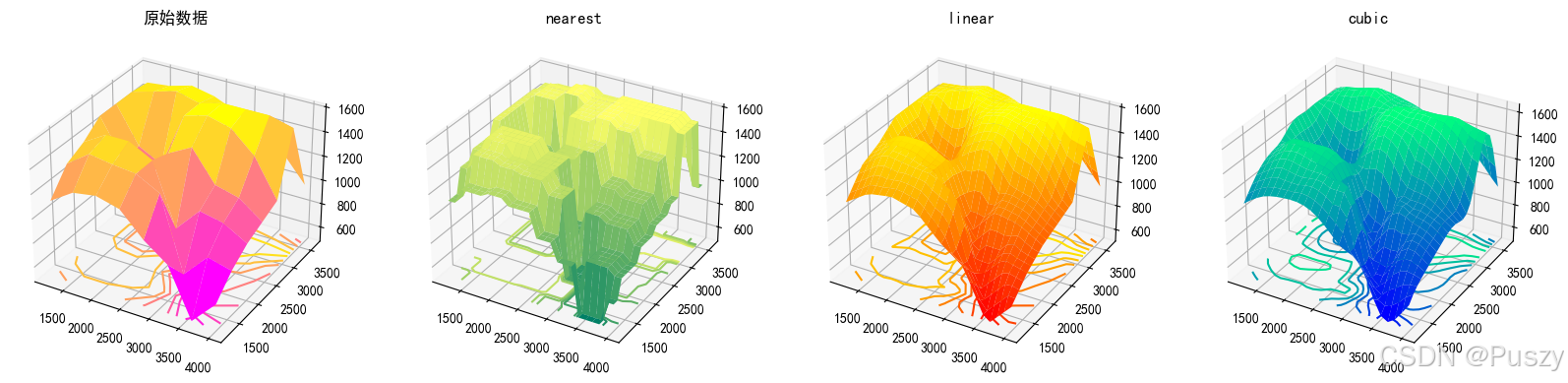
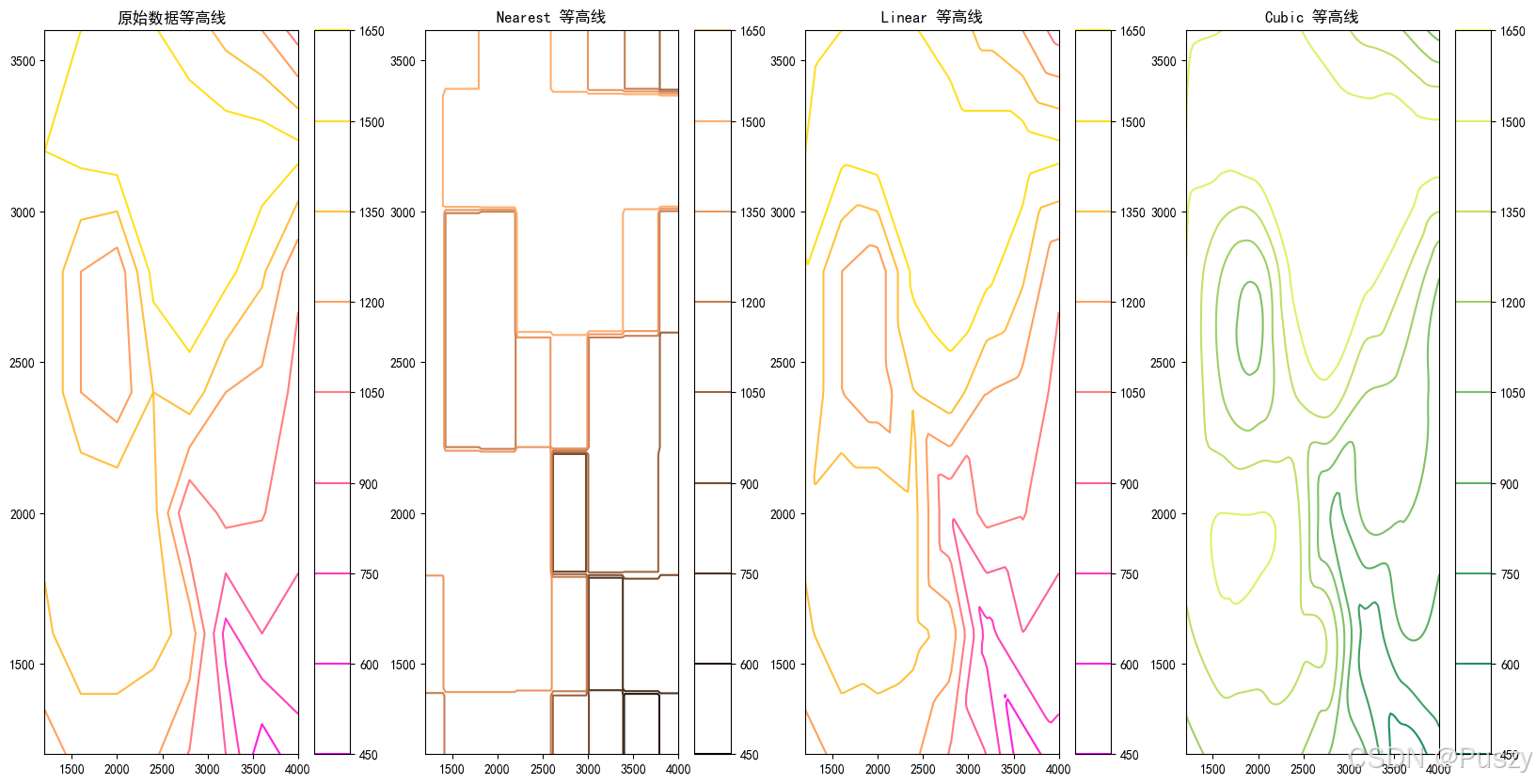
在这里插入图片描述

👉2.2.4、详细代码

# 导入 matplotlib 库的 pyplot 模块，用于绘制图形
import matplotlib.pyplot  as plt
# 导入 mpl_toolkits.mplot3d  中的 axes3d 模块，用于绘制 3D 图形
from mpl_toolkits.mplot3d  import axes3d
# 导入 matplotlib 库，用于设置图形的字体等属性
import matplotlib
# 导入 scipy.interpolate  中的 griddata 函数，用于进行数据插值
from scipy.interpolate  import griddata
# 导入 numpy 库，用于进行数值计算
import numpy as np

# 设置 matplotlib 的字体为黑体，字体加粗
matplotlib.rc("font",  family='SimHei', weight='bold')
# 设置 matplotlib 的字体为仿宋，用于正常显示中文标签
plt.rcParams['font.sans-serif']=['FangSong'] 
# 设置 matplotlib 正常显示负号
plt.rcParams['axes.unicode_minus']=False 

# 定义原始数据
# 创建一个从 1200 到 4000（包含），步长为 400 的一维数组，作为 x 轴的原始数据
x0 = np.array([i  for i in range(1200, 4001, 400)])
# 创建一个从 1200 到 3600（包含），步长为 400 的一维数组，作为 y 轴的原始数据
y0 = np.array([i  for i in range(1200, 3601, 400)])
# 使用 meshgrid 函数将 x0 和 y0 转换为二维网格坐标矩阵
X0, Y0 = np.meshgrid(x0,  y0)
# 定义 z 轴的原始数据，是一个二维数组
Z0 = np.array([ 
    [1130, 1250, 1280, 1230, 1040, 900, 500, 700],
    [1320, 1450, 1420, 1400, 1300, 700, 900, 850],
    [1390, 1500, 1500, 1400, 900, 1100, 1060, 950],
    [1500, 1200, 1100, 1350, 1450, 1200, 1150, 1010],
    [1500, 1200, 1100, 1550, 1600, 1550, 1380, 1070],
    [1500, 1550, 1600, 1550, 1600, 1600, 1600, 1550],
    [1480, 1500, 1550, 1510, 1430, 1300, 1200, 980],
])

# 定义插值函数
def interpolate(x0, y0, Z0, num=100, method='nearest'):
    # 生成插值点的坐标网格
    # 在 x0 的最小值和最大值之间均匀生成 num 个点
    x = np.linspace(x0.min(),  x0.max(),  num)
    # 在 y0 的最小值和最大值之间均匀生成 num 个点
    y = np.linspace(y0.min(),  y0.max(),  num)
    # 对原始数据的 x0 和 y0 进行网格化
    X0, Y0 = np.meshgrid(x0,  y0)
    # 对插值点的 x 和 y 进行网格化
    Xi, Yi = np.meshgrid(x,  y)
    # 使用 griddata 函数进行插值
    # 将原始数据的二维网格坐标矩阵展平，以及对应的 z 值展平
    # 根据插值点的网格坐标，使用指定的插值方法进行插值
    Zi = griddata((X0.flatten(),  Y0.flatten()),  Z0.flatten(),  (Xi, Yi), method=method)
    return Xi, Yi, Zi

# 定义插值方法列表
methods = ['nearest', 'linear', 'cubic']

# 定义颜色映射列表
Sequential = [ 'spring', 'summer', 'autumn', 'winter', 'cool',
               'Wistia', 'hot', 'afmhot', 'gist_heat', 'copper']

# 绘制原始数据的 3D 图形
# 创建一个大小为 20x10 的图形窗口
fig = plt.figure(figsize=(20,  10))
# 在图形窗口中添加一个 2 行 4 列的子图，位置为第 1 个
ax0 = fig.add_subplot(241,  projection='3d')
# 绘制 3D 曲面图，使用原始数据的网格坐标和 z 值，以及指定的颜色映射
ax0.plot_surface(X0,  Y0, Z0, cmap=Sequential[0])
# 设置子图的标题为“原始数据”
ax0.set_title(' 原始数据')
# 绘制 3D 等高线图，投影方向为 z 轴，偏移量为 z 值的最小值，使用指定的颜色映射
cset = ax0.contour(X0,  Y0, Z0, zdir='z', offset=np.min(Z0),  cmap=Sequential[0])

# 绘制不同插值方法的 3D 图形
for index, method in enumerate(methods):
    # 子图的索引从 2 开始
    index += 2
    # 在图形窗口中添加一个 2 行 4 列的子图，位置为当前索引对应的位置
    ax = fig.add_subplot(2,  4, index, projection='3d')
    # 调用插值函数进行插值，生成插值后的网格坐标和 z 值
    X, Y, Z = interpolate(x0, y0, Z0, num=25, method=method)
    # 绘制 3D 曲面图，使用插值后的网格坐标和 z 值，以及指定的颜色映射
    ax.plot_surface(X,  Y, Z, cmap=Sequential[index - 1])
    # 设置子图的标题为当前插值方法
    ax.set_title(f'{method}') 
    # 绘制 3D 等高线图，投影方向为 z 轴，偏移量为插值后 z 值的最小值，使用指定的颜色映射
    cset = ax.contour(X,  Y, Z, zdir='z', offset=np.min(Z),  cmap=Sequential[index - 1])

# 绘制原始数据的等高线图
# 创建一个大小为 20x10 的图形窗口
fig1 = plt.figure(figsize=(20,  10))
# 在图形窗口中添加一个 1 行 4 列的子图，位置为第 1 个
ax = fig1.add_subplot(1,  4, 1)
# 绘制等高线图，使用原始数据的网格坐标和 z 值，以及指定的颜色映射
contour = ax.contour(X0,  Y0, Z0, cmap=Sequential[0])
# 设置子图的标题为“原始数据等高线”
ax.set_title(f' 原始数据等高线')
# 为等高线图添加颜色条
fig1.colorbar(contour,  ax=ax)

# 绘制不同插值方法的等高线图
for index, method in enumerate(methods):
    # 在图形窗口中添加一个 1 行 4 列的子图，位置为当前索引加 2 对应的位置
    ax = fig1.add_subplot(1,  4, index + 2)
    # 调用插值函数进行插值，生成插值后的网格坐标和 z 值
    X, Y, Z = interpolate(x0, y0, Z0, num=100, method=method)
    # 绘制等高线图，使用插值后的网格坐标和 z 值，以及指定的颜色映射
    contour = ax.contour(X,  Y, Z, cmap=Sequential[index - 1])
    # 设置子图的标题为当前插值方法的大写形式加“ 等高线”
    ax.set_title(f'{method.capitalize()}  等高线')
    # 为等高线图添加颜色条
    fig1.colorbar(contour,  ax=ax)

# 显示所有绘制的图形
plt.show()

📚三、拟合（Fitting）

定义：拟合是通过已知数据点构建一个近似函数，使其在整体趋势上最接近数据分布，允许存在误差。其核心目标是揭示数据背后的潜在规律。

🚀3.1、二次多项式拟合

📘3.1.1、题目

对下面一组数据作二次多项式拟合，并作出数据点和拟合曲线的图形

x	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
y	-0.447	1.978	3.28	6.16	7.08	7.34	7.66	9.56	9.48	9.30	11.2

📘3.1.2、解决思路

Scikit-learn库提供了便捷的多项式拟合方案，使用Matplotlib绘制结果图，比较结果。

📈3.1.3、结果展示

在这里插入图片描述

3.1.4、详细代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# 整理后的数据点
x = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]).reshape(-1, 1)
y = np.array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 11.2])  # 修正了原始数据中的错误

fig=plt.figure(figsize=(40,6))  # 创建图形对象并设置大小
num_min=1  # 设置多项式最小阶数
num_max=10  # 设置多项式最大阶数
num=num_max-num_min  # 计算需要绘制的子图数量

# 循环拟合不同阶数的多项式
for i in range(num_min, num_max):
    # 创建二次多项式特征
    poly_features = PolynomialFeatures(degree=i, include_bias=False)
    # 转换特征
    x_poly = poly_features.fit_transform(x)
    # 创建线性回归模型
    model = LinearRegression()
    # 拟合模型
    model.fit(x_poly, y)
    ax=fig.add_subplot(1, num, i-num_min+1)  # 添加子图
    # 绘制原始数据点
    ax.scatter(x, y, color='blue', label='原始数据')
    # 提取系数和截距
    coef = model.coef_
    intercept = model.intercept_
    # 构建多项式表达式
    poly_expr = f"{intercept:.3f}"
    for j in range(i):
        poly_expr += f" + {coef[j]:.3f}x^{j+1}"
    print(f"多项式阶数 {i}: y = {poly_expr}")  # 打印多项式表达式
    # 绘制拟合直线
    x_line = np.linspace(x.min(), x.max(), 100).reshape(100, 1)  # 生成连续的x值
    x_line_poly = poly_features.transform(x_line)  # 转换为多项式特征
    y_pred = model.predict(x_line_poly)  # 预测y值
    ax.plot(x_line, y_pred, color='red', label='拟合曲线')  # 绘制拟合曲线
    # 添加图例和标签
    ax.set_title(f'多项式阶数{i}')  # 设置子图标题

plt.show()  # 显示图形

🚀3.2 非线性拟合方案

📘3.2.1、(Logistic）传染病模型

在一次传染病中，已知t时刻的染病人数满足模型 $\frac{1}{a + be^{ct}}$ 公共部门每隔5天记录一次传染病的人数，具体见表1，试利用拟合方法确定参数 a,b,c。
表1传染人数记录

天数	0	5	10	15	20	25	30
感染人数（单位：百人）	0.2	0.4	0.5	0.9	1.5	2.4	3.1
天数	35	40	45	50	55	60
感染人数（单位：百人）	3.8	4.1	4.2	4.5	4.4	4.5

📘3.2.2、解决思路

对于非线性拟合，可使用Python的scipy.optimize库来进行高效拟合，curve_fit 通过最小化模型预测值和实际观测值之间的平方差来估计这些参数。通过设置初始猜测值 p0 和参数边界 bounds，可以提高拟合的稳定性和准确性。curve_fit 返回最优参数 popt 和参数协方差矩阵 pcov。

📈3.2.3、结果展示

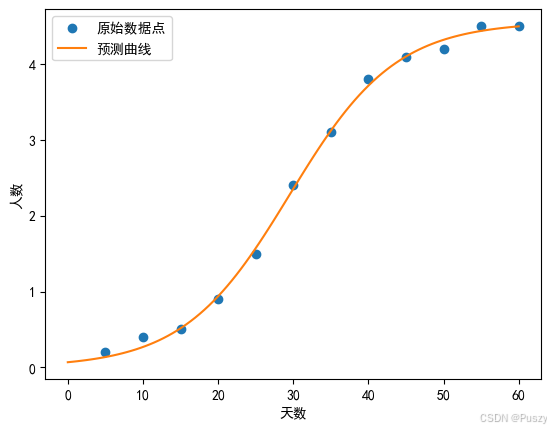
在这里插入图片描述

👉3.2.4、详细代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 从文件中整理出的数据点，表示每隔5天记录的感染人数（单位：百人）
t = np.array([5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60])  # 天数
I_actual = np.array([0.2, 0.4, 0.5, 0.9, 1.5, 2.4, 3.1, 3.8, 4.1, 4.2, 4.5, 4.5])  # 感染人数（百人）

# 定义模型函数，这里使用的是逻辑斯蒂模型
def I(t, a, b, c):
    # 逻辑斯蒂模型的公式
    return 1 / (a + b * np.exp(-c * t))

# 使用 curve_fit 进行拟合，p0是参数的初始猜测值，bounds是参数的边界
popt, pcov = curve_fit(I, t, I_actual, p0=[1, 1, 0.1], bounds=([0, 0, 0], [np.inf, np.inf, np.inf]))

# 获取最优参数
a, b, c = popt

# 打印拟合得到的最优参数值
print(f"Optimized parameters: a={a:.4f}, b={b:.4f}, c={c:.4f}")

# 绘制拟合曲线
# 生成一个从0到60的等间隔数列，用于绘制拟合曲线
t_fit = np.linspace(0, 60, 100)
# 计算拟合曲线在t_fit对应的I值
I_fit = I(t_fit, a, b, c)

# 绘制原始数据点和拟合曲线
plt.plot(t, I_actual, 'o', label='原始数据点')  # 绘制原始数据点
plt.plot(t_fit, I_fit, label='预测曲线')  # 绘制拟合曲线

# 设置x轴和y轴的标签
plt.xlabel('天数')
plt.ylabel('人数')

# 显示图例
plt.legend()

# 显示绘制的图形
plt.show()