LCR 051.二叉树中最大路径和

目录

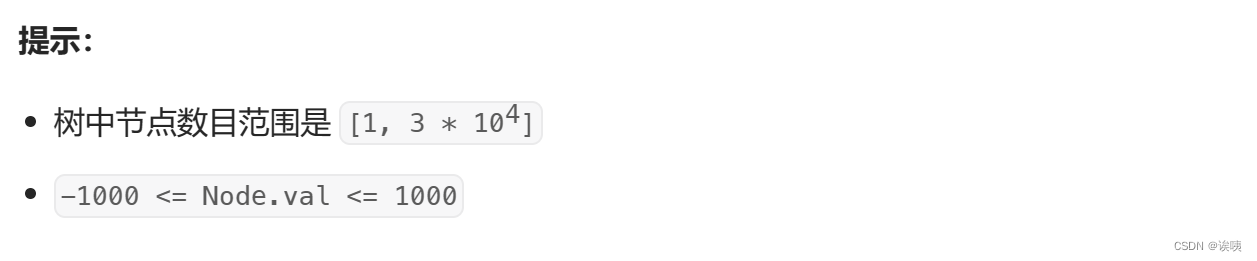
题目描述

思路解析

AC代码

---

题目描述

LCR 051.二叉树中最大路径和

思路解析

这道题是一道路径规划题。如果，我们将其视作图。从枚举的角度上来说 弗洛伊德算法 将是很好的一种解决手段。但是，我们的树中节点的规模告诉我们，这是痴心妄想的。

根据题目意思，一条路径序列中的节点仅出现一次也就表明这条路线是单一的，不会出现交汇的情况。那么我们不妨考虑简单情况，因为此时我们面对处理树的手段还有DFS。我们可以通过DFS来缩小问题规模。

那么，我们很快就能获取到三种情况：

1. 向左子树延申，可上传

2. 向右子树延申，可上传

3. 链接左右子树，也意味着路径规划结束，不可能在上传

最终的答案，就在这三种情况中诞生。

AC代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int maxSum = INT_MIN;

public:
    int maxGain(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }
        
        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = max(maxGain(node->left), 0);   //向左延申
        int rightGain = max(maxGain(node->right), 0); //向右延申

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node->val + leftGain + rightGain;//连接左右，且不可上传

        // 更新答案
        maxSum = max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node->val + max(leftGain, rightGain);
    }

    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};