表达式计算

题目表述及样子示意

 

 

题意分析

这道题，咋一眼看很简单，因为就是进行几乎是我们小学时代就会的基本运算。

但是仔细一想，这道题难度不小，问题出现在运算的次序上，符号的解析上。因为对于我们人脑来说处理这些式子轻而易举，但是对于计算机就不行。为什么呢？计算机面对一个表达式对它的认知只是字符串。而不能如同人脑一般提起对式子预处理。

所以我们需要一个方式，让计算机也学会处理表达式中的信息。大概有两点：1.运算次序信息处理；2.符号解析（运算符、运算数、正负号）

当然，当你了解过算法、看过一些算法书籍，大多数市面做法都采用“双栈法”。但是我们今天不采用“双栈法”，而是另外一种数据化翻译方式。

在我们的认知中，对于 a + b，我们最关注的是什么，或者说我们最先关注的是什么？很明显是运算符号‘+’；于是我们可以根据我们的注意点来画出一幅图。

 接下来，我们考虑 对于式子 a + b * c呢？

我们可以画出下面的图

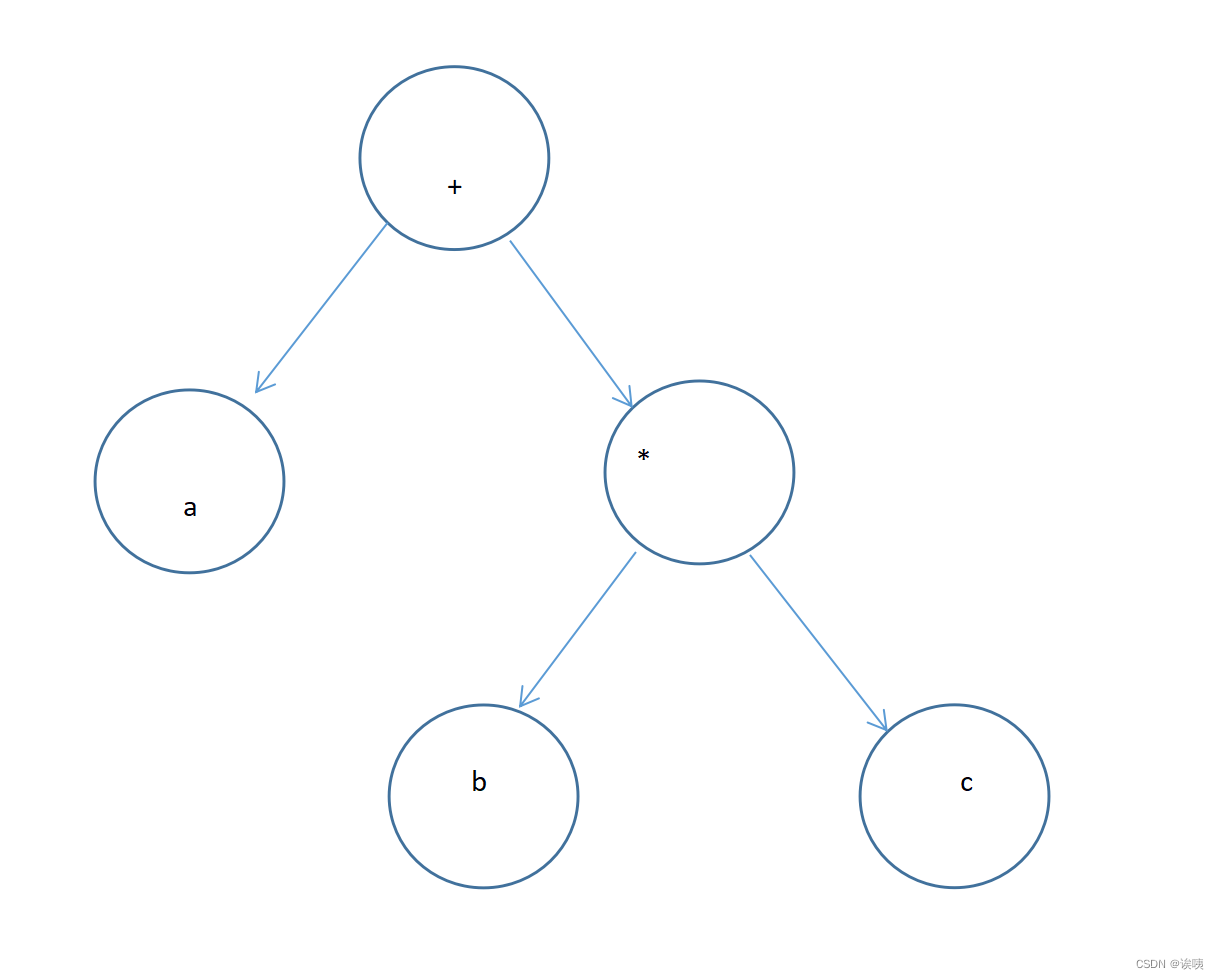
没错，我们的反应应该是 a + ‘？’，‘？’是什么？没错‘？’是 b*c。也就是我们要知道最终的答案结果我们需要先知道‘？’数值才能知道答案，所以我们有了“优先级” 。

那我们可以有下面的表格（按优先级）：

 但是，我们很会发现一个问题‘（）’。括号它不影响数值，但是它影响优先级啊！

这恰巧也是我们需要关注的信息之一，于是我们能反应到本身的优先级还不够用，需要一个额外的优先级来反应‘（）’的影响。

于是又有了下表格：

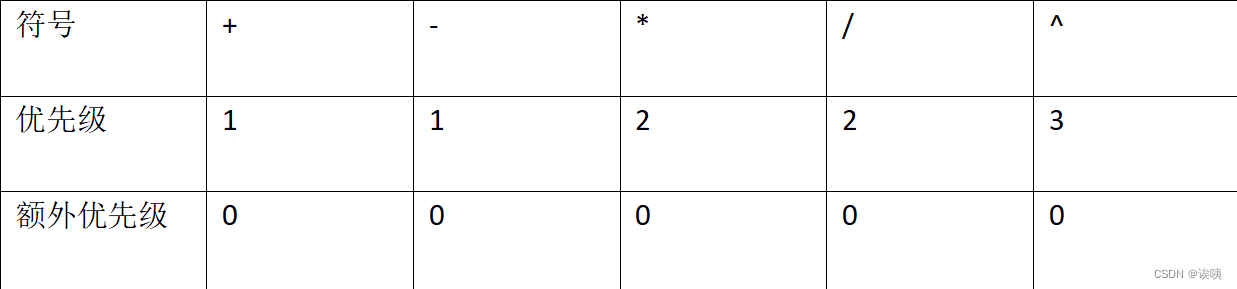
当我们遇到‘（’时，额外优先级 +100，遇到‘）’时，额外优先级 -100，以此来反应总优先运算级别 。然后我们需要先选取优先级别低的运算符号将运算式子拆解成两个子问题求解。那么我们可以采用递归设计。

于是我们可以有一下设计：

#include <iostream>
#include <cstdlib>
#include <stack>
#include <queue>
#include <set>
#include <unordered_set>
#include <algorithm>
#include <cmath>
using namespace std;

int calcu(string& s, int l, int r);

int main(){

        string str;

        cin >> str;

        int n = str.size();

        calcu(str, 0, n);

        return 0;

}

搭建完框架，我们开始填充细节代码:

在calcu（...）中，我们需要做以下事情：

1.遍历寻找优先级最低的运算符号，以其为分隔符，将式子拆解成左右两个子问题；

2.遇到'('额外权重 +100，遇到‘）’额外权重 -100；

3.运算级别相同，应该符合我们人的关注顺序（运算顺序），从左向右关注；

第一件事情，意味着我们需要标记出最小运算符位置，其次我们需要思考一个问题初始值。

因为我们需要找到最小值，诶赋值成“无穷大”就不错，我们思考以下数字的优先级，显然，数字的优先级（我们的关注点要低）要大，故此‘无穷大’可行。

对于第三件事情，赋值无穷大能合理吗？我们知道从左向右关注，也就是从右向左运算，我们需要找到最右边的最低运算符。那么一定是 ‘... >= ...’;如果运算符和数字都是INF，那么就算是数字也会符合条件。所以为了让数字是第一优先级，它的初始值必须比运算符高。所以运算符最大要为INF-1

综上，我们需要最低位置的优先级、位置；现在遍历的符号优先级，以及其额外优先级；

#define INF 0x3f3f3f3f

int calcu(string& s, int l, int r){

        int pos = -1, pri = INF-1, cur_pri = INF, temp_pri = 0;

        for(int i = l; i < r; ++i){

                cur_pri = INF;

                switch(s[i]){

                        case '(': temp_pri += 100; break;

                        case  ')':temp_pri  -= 100; break;

                        case '+':

                        case '-': cur_pri = temp_pri + 1; break;

                        case '*':

                        case '/': cur_pri =temp_pri + 2; break;

                        case '^': cur_pri =temp_pri + 3; break;

                }

                if(pri >= cur_pri){

                        pri = cur_pri;

                        pos = i;

                }

        }

       

        if(pos == -1){//区间内没有最低运算符，注意这不代表只有数字,因为可能还有括号

                             //或者没有任何字符，不要想当然，pos只标记五种符号

                int ans = 0;

                for(int i = l; i < r; ++i){

                        if('0' <= s[i] && s[i] <= '9')ans = ans * 10 + s[i] - '0';

                }

                return ans;

        }

        //注意区间是左闭右开

    int num_l = calcu(s, l, pos);
    int num_r = calcu(s, pos + 1, r);

    switch (s[pos]) {
    case '+': return num_l + num_r;
    case '-': return num_l - num_r;
    case '*': return num_l * num_r;
    case '/': return num_l / num_r;
    case '^': return static_cast<int>(pow(num_l, num_r));
    }

        //为了编译成功，或者是一种习惯，本句其实没有用。

        return 0;

}

好，至此我们的代码已经完善了差不多了。现在还有一个问题没有解决，也就是现在的程序还有一个小bug。还记得两件事情吗？我们现在其实只做了优先级分析，以及大部分符号解析，但是正负号呢？

没错我们上述代码中，没有处理 ‘-’的含义是什么，是运算符还是表示取反？

所以我们要思考，取反如何表示、解析。

其实，这个问题没那么难，因为取反也有优先级，在数学上是这样理解的。而且还相当高，也就是如果检测到‘-/+’时，我们需要额外检测他们的含义。

什么时候时取反呢？其实就是前面的符号不是数字的时候但不为‘）’（是非括号其他运算符)，或者前面又没任何数字；

#define INF 0x3f3f3f3f

int calcu(string& s, int l, int r) {
    int pos = -1, pri = INF - 1, cur_pri = INF, temp_pri = 0;

    for (int i = l; i < r; ++i) {
        cur_pri = INF;//
        switch (s[i]) {
        case '(':temp_pri += 100; break;
        case ')':temp_pri -= 100; break;
        case '+':
        case '-':
            cur_pri = temp_pri + 1;
            if (i == 0 || ('0' > s[i - 1] || s[i - 1] > '9') && s[i - 1] != ')') cur_pri += 1000;//
            break;
        case '*':
        case '/':cur_pri = temp_pri + 2; break;
        case '^':cur_pri = temp_pri + 3; break;
        }

        if (pri >= cur_pri) {
            pri = cur_pri;
            pos = i;
        }
    }

    if (pos == -1) {
        int num = 0;
        for (int i = l; i < r; ++i) {
            if ('0' <= s[i] && s[i] <= '9')num = num * 10 + (s[i] - '0'); //
        }
        return num;
    }

    int num_l = calcu(s, l, pos);
    int num_r = calcu(s, pos + 1, r);

    switch (s[pos]) {
    case '+': return num_l + num_r;
    case '-': return num_l - num_r;
    case '*': return num_l * num_r;
    case '/': return num_l / num_r;
    case '^': return static_cast<int>(pow(num_l, num_r));
    }

    return 0;
}

int main() {
    string s;
    cin >> s;
    cout << calcu(s, 0, s.size());
    return 0;
}

但是，前面没有很任何数字其实也可以认为是 0 +/- 数字；所以也可以不需要判断这种情况；

最后的代码，也可以这样子表述

if (i > 0 && ('0' > s[i - 1] || s[i - 1] > '9') && s[i - 1] != ')') 

#include <iostream>
#include <cstdlib>
#include <stack>
#include <queue>
#include <set>
#include <unordered_set>
#include <algorithm>
#include <cmath>
using namespace std;

//寻找最低优先级运算符号；
//以此为分界线，对左右两个部分进行计算；
//
//注意 ‘-’是运算符还是取反符号？ 取反符 == 前一字符为非括号运算符
//‘（）‘会改变优先级，所以需要引入附加权重的概念

#define INF 0x3f3f3f3f

int calcu(string & s, int l, int r) {
	int pos = -1, pri = INF - 1, cur_pri = INF, temp_pri = 0;
	
	for (int i = l; i < r; ++i) {
		cur_pri = INF;//
		switch (s[i]) {
			case '(':temp_pri += 100; break;
			case ')':temp_pri -= 100; break;
			case '+':
			case '-':
				cur_pri = temp_pri + 1;
				if (i > 0 && ('0' > s[i - 1] || s[i - 1] > '9') && s[i - 1] != ')') cur_pri += 1000;//
				break;
			case '*':
			case '/':cur_pri = temp_pri + 2; break;
			case '^':cur_pri = temp_pri + 3; break;
		}

		if (pri >= cur_pri) {
			pri = cur_pri;
			pos = i;
		}
	}

	if (pos == -1) {
		int num = 0;
		for (int i = l; i < r; ++i) {
			 num = num * 10 + (s[i] - '0'); //
		}
		return num;
	}

	int num_l = calcu(s, l, pos);
	int num_r = calcu(s, pos + 1, r);

	switch (s[pos]) {
	case '+': return num_l + num_r;
	case '-': return num_l - num_r;
	case '*': return num_l * num_r;
	case '/': return num_l / num_r;
	case '^': return static_cast<int>( pow(num_l, num_r) );
	}

	return 0;
}

int main() {
	string s;
	cin >> s;
	cout << calcu(s, 0, s.size());
	return 0;
}