虽然DDPG算法是离线策略算法,但是它的训练非常不稳定,收敛性较差,对超参数比较敏感,也难以适应不同的环境,所以一个想法就是提升策略的随机性。2018年,一个更加稳定的离线策略算法Soft Actor-Critic(SAC)被提出。SAC的前身是Soft Q-learning,它们都属于最大熵强化学习的范畴。
熵(entropy)表示对一个随机变量的随机程度的度量。具体而言,如果X是一个随机变量,而且它的概率密度函数为p,那么它的熵H就被定义为:
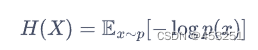
在强化学习中,我们使用![]() 来表示策略π在状态s下的随机程度。
来表示策略π在状态s下的随机程度。
最大熵强化学习的思想就是除了要最大化累计奖励,还要使得策略更加随机。如此,强化学习的目标中就加入了一项熵的正则项,定义为:

其中α是一个正则化的系数,用来控制熵的重要程度。
熵的正则化增加了强化学习算法的探索程度,α越大,探索性就越强,有助于加速后续的策略学习,并减少策略陷入较差的局部最优的可能性。传统强化学习和最大熵强化学习的区别如下图: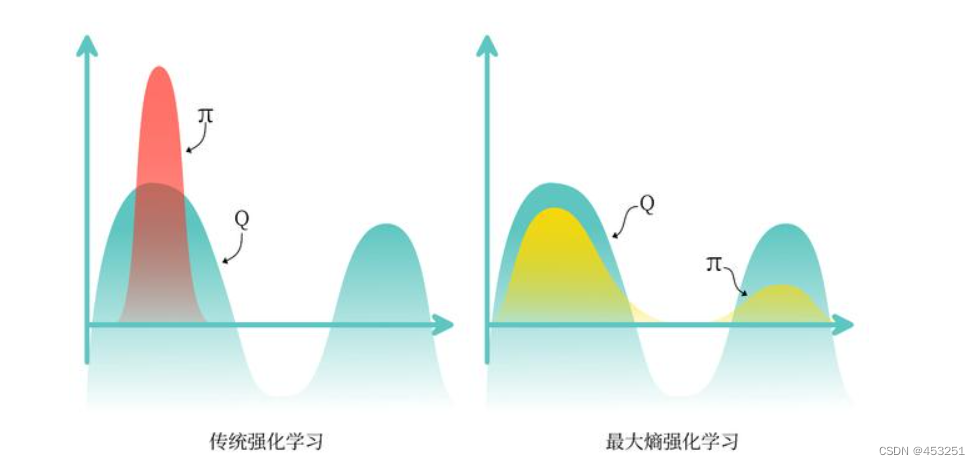
在最大熵强化学习框架中,由于目标函数发生了变化,其他的一些定义也有相应的变化。首先,我们先看一下soft贝尔曼方程:
![]()
其中,加入熵正则项后,状态价值函数被写为:

于是,根据soft贝尔曼方程,在有限的状态和动作空间下,soft策略评估可以收敛到策略π的soft Q函数。然后,根据如下soft策略提升公式可以改进策略:

这个公式是指通过最小化动作分布的KL散度来改进策略,括号中的右半部分表示基于当前值函数和归一化因子的指数型动作分布,通过最小化 KL 散度,我们能够使改善后的策略更接近于基于当前值函数的指数型动作分布,从而提高整体策略的性能。
重复交替使用 Soft 策略评估和 Soft 策略提升,最终策略可以收敛到最大熵强化学习目标中的最优策略。但该 Soft 策略迭代方法只适用于表格型(tabular)设置的情况,即状态空间和动作空间是有限的情况。在连续空间下,我们需要通过参数化函数和策略来近似这样的迭代。
在 SAC 算法中,我们为两个动作价值函数Q(参数分别ω1和ω2)和一个策略函数π(参数为θ)建模。基于 Double DQN 的思想,SAC 使用两个Q网络,但每次用Q网络时会挑选一个Q值小的网络,从而缓解Q值过高估计的问题。任意一个函数Q的损失函数为:

其中,R是策略过去收集的数据,其实该损失函数就是利用训练Q网络的输出减去时序差分目标(加上熵正则项)估计的Q值的均方误差损失,(时序差分目标既可以估计Q值也可以估计V值)。由于SAC是一个离线策略算法,为了让训练更加稳定,这里使用了目标Q网络![]() ,同样是两个目标Q网络,与两个Q网络一一对应,且目标Q网络的更新方式与DDPG的更新方式一样。
,同样是两个目标Q网络,与两个Q网络一一对应,且目标Q网络的更新方式与DDPG的更新方式一样。
同时,策略π的损失函数可由KL散度得到,化简后为:
![]()
可以理解为最大化函数V,因为有![]()
对于连续动作空间的环境,SAC算法的策略网络输出高斯分布的均值和标准差,但是根据高斯分布来采样动作的过程是不可导的(是因为高斯分布的采样是通过随机抽取标准正态分布(也称为高斯分布的变量)加上平均值和标准差的乘积得到的。这个过程中包含了随机性,因此不能通过求导来表示)。因此,我们需要用到重参数化技巧,重参数化的做法是先从一个单位高斯分布![]() 采样,再把采样值乘以标准差后加上均值。这样就可以认为是从策略高斯分布采样,并且这个采样动作的过程对于策略函数是可导的,可以将该策略函数表示为
采样,再把采样值乘以标准差后加上均值。这样就可以认为是从策略高斯分布采样,并且这个采样动作的过程对于策略函数是可导的,可以将该策略函数表示为![]() ,其中
,其中![]() 是一个噪声随机变量。同时考虑两个函数Q,重写策略的损失函数为:
是一个噪声随机变量。同时考虑两个函数Q,重写策略的损失函数为:

同时,在SAC算法中,如何选择熵正则项的系数非常重要。在不同的状态下需要不同大小的熵:在最优动作的不确定某个状态下,熵的取值应该大一点;而在某个最优动作比较确定的状态小,熵的取值就可以小一点。所以,考虑到需要调整熵正则项,SAC将强化学习的目标改写为一个带约束条件的优化问题:
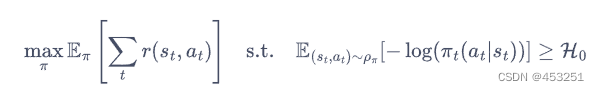
也就是最大化期望回报的同时,我们也需要将熵控制在一定范围内,我们约数熵的均值大于H0。化简后,我们可以得到α的损失函数:

即当策略的熵低于目标值H0时,训练目标L(α)会使的值增大,进而在上述最小化损失函数的过程中增加了策略熵对应项的重要性;而当策略的熵高于目标值时,训练目标会使的值减小,进而使得策略训练时更专注于价值提升。
首先,我们在倒立摆环境下进行试验
导入库
import random
import gym
import numpy as np
from tqdm import tqdm
import torch
import torch.nn.functional as F
from torch.distributions import Normal
import matplotlib.pyplot as plt
import rl_utils接下来定义策略网络和价值网络。由于处理的是与连续动作交互的环境,策略网络输出一个高斯分布的均值和标准差来表示动作分布;而价值网络的输入是状态和动作的拼接向量,输出一个实数来表示动作价值。
class PolicyNetContinuous(torch.nn.Module):
def __init__(self,state_dim,hidden_dim,action_dim,action_bound):
super(PolicyNetContinuous,self).__init__()
self.fc1=torch.nn.Linear(state_dim,hidden_dim)
self.fc_mu=torch.nn.Linear(hidden_dim,action_dim)
self.fc_std=torch.nn.Linear(hidden_dim,action_dim)
self.action_bound=action_bound
def forward(self,x):
x=F.relu(self.fc1(x))
mu=self.fc_mu(x)
std=F.softplus(self.fc_std(x))
#创建一个正态分布对象,作为动作空间
dist=Normal(mu,std)
#动作空间采样,得到样本,样本是动作值,代表连续空间中对应的动作
normal_sample=dist.rsample() #rsample()是重参数化采样
#计算样本的对数概率密度
log_prob=dist.log_prob(normal_sample)
#将动作约数在[-1,1]
action=torch.tanh(normal_sample)
#计算tanh_normal分布的对数概率密度
#限制动作范围会影响到动作的概率密度函数。这是因为 tanh 函数的导数在边界点上接近于零,这可能导致在这些点上计算的概率密度非常小,甚至接近于零。这会导致梯度消失,从而影响模型的训练效果。
#为了解决这个问题,可以使用公式 log(1 - tanh^2(x) + ε) 来重新计算对数概率密度,其中 ε 是一个较小的常数(在这里是 1e-7),用于避免取对数时的除零错误。这样可以保持对数概率密度的合理值,并避免梯度消失的问题。因此,在该代码中,使用该公式重新计算 log_prob。
log_prob=log_prob - torch.log(1-torch.tanh(action).pow(2) + 1e-7)
#得到动作的范围
action=action * self.action_bound
return action, log_prob
class QValueNetContinuous(torch.nn.Module):
def __init__(self,state_dim,hidden_dim,action_dim):
super(QValueNetContinuous,self).__init__()
self.fc1=torch.nn.Linear(state_dim+action_dim,hidden_dim)
self.fc2=torch.nn.Linear(hidden_dim,hidden_dim)
self.fc_out=torch.nn.Linear(hidden_dim,1)
def forward(self,x,a):
cat=torch.cat([x,a],dim=1)
x=F.relu(self.fc1(cat))
x=F.relu(self.fc2(x))
return self.fc_out(x)然后我们来看一下 SAC 算法的主要代码。如 14.4 节所述,SAC 使用两个 Critic 网络和来使 Actor 的训练更稳定,而这两个 Critic 网络在训练时则各自需要一个目标价值网络。因此,SAC 算法一共用到 5 个网络,分别是一个策略网络、两个价值网络和两个目标价值网络。
class SACContinuous:
"""处理连续动作的SAC算法"""
def __init__(self,state_dim,hidden_dim,action_dim,action_bound,actor_lr,critic_lr,alpha_lr,target_entropy,tau,gamma,device):
self.actor=PolicyNetContinuous(state_dim,hidden_dim,action_dim,action_bound).to(device) #策略网络
self.critic_1=QValueNetContinuous(state_dim,hidden_dim,action_dim).to(device) #第一个Q网络
self.critic_2=QValueNetContinuous(state_dim,hidden_dim,action_dim).to(device) #第二个Q网络
self.target_critic_1=QValueNetContinuous(state_dim,hidden_dim,action_dim).to(device) #第一个目标Q网络
self.target_critic_2=QValueNetContinuous(state_dim,hidden_dim,action_dim).to(device) #第二个目标Q网络
#令目标Q网络的参数和Q网络一样
self.target_critic_1.load_state_dict(self.critic_1.state_dict())
self.target_critic_2.load_state_dict(self.critic_2.state_dict())
self.actor_optimizer=torch.optim.Adam(self.actor.parameters(),lr=actor_lr)
self.critic_1_optimizer=torch.optim.Adam(self.critic_1.parameters(),lr=critic_lr)
self.critic_2_optimizer=torch.optim.Adam(self.critic_2.parameters(),lr=critic_lr)
#使用alpha的log值,可以使训练结果比较稳定
self.log_alpha=torch.tensor(np.log(0.01),dtype=torch.float)
self.log_alpha.requires_grad=True #可以对alpha求梯度
self.log_alpha_optimizer=torch.optim.Adam([self.log_alpha],lr=alpha_lr)
self.target_entropy=target_entropy #目标熵的大小
self.gamma=gamma
self.tau=tau
self.device=device
def take_action(self,state):
state=torch.tensor([state],dtype=torch.float).to(self.device)
action=self.actor(state)[0]
return [action.item()]
def calc_target(self,rewards,next_states,dones): #计算目标Q值
next_actions,log_prob=self.actor(next_states)
#计算熵,注意这里是有个负号的
entropy=-log_prob
q1_value=self.target_critic_1(next_states,next_actions)
q2_value=self.target_critic_2(next_states,next_actions)
#注意entropy自带负号
next_value=torch.min(q1_value,q2_value) + self.log_alpha.exp() * entropy
td_target=rewards + self.gamma * next_value *(1-dones)
return td_target
def soft_update(self,net,target_net):
for param_target, param in zip(target_net.parameters(),net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)
def update(self,transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
#和之前章节一样,对倒立摆的奖励进行重塑以便训练
rewards=(rewards + 8.0) / 8.0
#更新两个Q网络
td_target=self.calc_target(rewards,next_states,dones)
#Q网络输出值和目标值的均方差
critic_1_loss=torch.mean(F.mse_loss(self.critic_1(states,actions),td_target.detach()))
critic_2_loss=torch.mean(F.mse_loss(self.critic_2(states,actions),td_target.detach()))
self.critic_1_optimizer.zero_grad()
critic_1_loss.backward()
self.critic_1_optimizer.step()
self.critic_2_optimizer.zero_grad()
critic_2_loss.backward()
self.critic_2_optimizer.step()
#更新策略网络
new_actions, log_prob=self.actor(states)
entropy= -log_prob
q1_value=self.critic_1(states,new_actions)
q2_value=self.critic_2(states,new_actions)
#最大化价值,所以误差为价值函数加负号
actor_loss=torch.mean(-self.log_alpha.exp() * entropy - torch.min(q1_value,q2_value))
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
#更新alpha值
#利用梯度下降自动调整熵正则项
alpha_loss=torch.mean((entropy - self.target_entropy).detach() *self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()
#软更新目标网络
self.soft_update(self.critic_1,self.target_critic_1)
self.soft_update(self.critic_2,self.target_critic_2)设置超参数,进行试验
env_name = 'Pendulum-v1'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0] # 动作最大值
random.seed(0)
np.random.seed(0)
env.reset(seed=0)
torch.manual_seed(0)
actor_lr = 3e-4
critic_lr = 3e-3
alpha_lr = 3e-4
num_episodes = 100
hidden_dim = 128
gamma = 0.99
tau = 0.005 # 软更新参数
buffer_size = 100000
minimal_size = 1000
batch_size = 64
target_entropy = -env.action_space.shape[0]
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = SACContinuous(state_dim, hidden_dim, action_dim, action_bound,
actor_lr, critic_lr, alpha_lr, target_entropy, tau,
gamma, device)
return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes,
replay_buffer, minimal_size,
batch_size)
绘图
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
可以发现,SAC 在倒立摆环境中的表现非常出色。SAC 算法原本是针对连续动作交互的环境提出的,那一个比较自然的问题便是:SAC 能否处理与离散动作交互的环境呢?答案是肯定的,但是我们要做一些相应的修改。首先,策略网络和价值网络的网络结构将发生如下改变:
- 策略网络的输出修改为在离散动作空间上的 softmax 分布;
- 价值网络直接接收状态和离散动作空间的分布作为输入。
定义价值网络和策略网络
class PolicyNet(torch.nn.Module):
def __init__(self,state_dim,hidden_dim,action_dim):
super(PolicyNet,self).__init__()
self.fc1=torch.nn.Linear(state_dim,hidden_dim)
self.fc2=torch.nn.Linear(hidden_dim,action_dim)
def forward(self,x):
x=F.relu(self.fc1(x))
return F.softmax(self.fc2(x),dim=1)
class QValueNet(torch.nn.Module):
"""只有一层隐藏层的Q网络"""
def __init__(self,state_dim,hidden_dim,action_dim):
super(QValueNet,self).__init__()
self.fc1=torch.nn.Linear(state_dim,hidden_dim)
self.fc2=torch.nn.Linear(hidden_dim,action_dim)
def forward(self,x):
x=F.relu(self.fc1(x))
return self.fc2(x)该策略网络输出一个离散的动作分布,所以在价值网络的学习过程中,不需要再对下一个动作a(t+1)进行采样,而是直接通过概率计算来得到下一个状态的价值。同理,在α的损失函数计算中,也不需要再对动作进行采样。
class SAC:
''' 处理离散动作的SAC算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
alpha_lr, target_entropy, tau, gamma, device):
# 策略网络
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
# 第一个Q网络
self.critic_1 = QValueNet(state_dim, hidden_dim, action_dim).to(device)
# 第二个Q网络
self.critic_2 = QValueNet(state_dim, hidden_dim, action_dim).to(device)
self.target_critic_1 = QValueNet(state_dim, hidden_dim,
action_dim).to(device) # 第一个目标Q网络
self.target_critic_2 = QValueNet(state_dim, hidden_dim,
action_dim).to(device) # 第二个目标Q网络
# 令目标Q网络的初始参数和Q网络一样
self.target_critic_1.load_state_dict(self.critic_1.state_dict())
self.target_critic_2.load_state_dict(self.critic_2.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
lr=actor_lr)
self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(),
lr=critic_lr)
self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(),
lr=critic_lr)
# 使用alpha的log值,可以使训练结果比较稳定
self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float)
self.log_alpha.requires_grad = True # 可以对alpha求梯度
self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha],
lr=alpha_lr)
self.target_entropy = target_entropy # 目标熵的大小
self.gamma = gamma
self.tau = tau
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
# 计算目标Q值,直接用策略网络的输出概率进行期望计算
def calc_target(self, rewards, next_states, dones):
next_probs = self.actor(next_states)
next_log_probs = torch.log(next_probs + 1e-8)
#用next_log_probs的期望作为熵,因为动作是离散的
#keepdim=True是保持维度不变
entropy = -torch.sum(next_probs * next_log_probs, dim=1, keepdim=True)
q1_value = self.target_critic_1(next_states)
q2_value = self.target_critic_2(next_states)
#同样地,利用期望
min_qvalue = torch.sum(next_probs * torch.min(q1_value, q2_value),
dim=1,
keepdim=True)
next_value = min_qvalue + self.log_alpha.exp() * entropy
td_target = rewards + self.gamma * next_value * (1 - dones)
return td_target
def soft_update(self, net, target_net):
for param_target, param in zip(target_net.parameters(),
net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) +
param.data * self.tau)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device) # 动作不再是float类型
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
# 更新两个Q网络
td_target = self.calc_target(rewards, next_states, dones)
critic_1_q_values = self.critic_1(states).gather(1, actions)
critic_1_loss = torch.mean(
F.mse_loss(critic_1_q_values, td_target.detach()))
critic_2_q_values = self.critic_2(states).gather(1, actions)
critic_2_loss = torch.mean(
F.mse_loss(critic_2_q_values, td_target.detach()))
self.critic_1_optimizer.zero_grad()
critic_1_loss.backward()
self.critic_1_optimizer.step()
self.critic_2_optimizer.zero_grad()
critic_2_loss.backward()
self.critic_2_optimizer.step()
# 更新策略网络
probs = self.actor(states)
log_probs = torch.log(probs + 1e-8)
# 直接根据概率计算熵
entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True) #
q1_value = self.critic_1(states)
q2_value = self.critic_2(states)
min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value),
dim=1,
keepdim=True) # 直接根据概率计算期望
actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue)
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# 更新alpha值
alpha_loss = torch.mean(
(entropy - target_entropy).detach() * self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()
self.soft_update(self.critic_1, self.target_critic_1)
self.soft_update(self.critic_2, self.target_critic_2)设置超参数,进行试验
actor_lr = 1e-3
critic_lr = 1e-2
alpha_lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
tau = 0.005 # 软更新参数
buffer_size = 10000
minimal_size = 500
batch_size = 64
target_entropy = -1
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.reset(seed=0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = SAC(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, alpha_lr,
target_entropy, tau, gamma, device)
return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes,
replay_buffer, minimal_size,
batch_size)
绘图
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
可以发现,SAC 在离散动作环境车杆下具有完美的收敛性能,并且其策略回报的曲线十分稳定,这体现出 SAC 可以在离散动作环境下平衡探索与利用的优秀性质。























 1346
1346

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








