教你用纯 Numpy 实现神经网络：从数学公式到可运行代码, 实现双输入单隐藏层分类器

本文链接：https://blog.youkuaiyun.com/qq_70350287/article/details/146361014

1. 前置知识准备

调用框架如乘快车，手撸代码似拆引擎 —— 唯有亲手解构神经网络的每个齿轮，才能真正理解其运转逻辑。因此，我们将构建一个简单的 2 层神经网络（1 个隐藏层），结构如下：

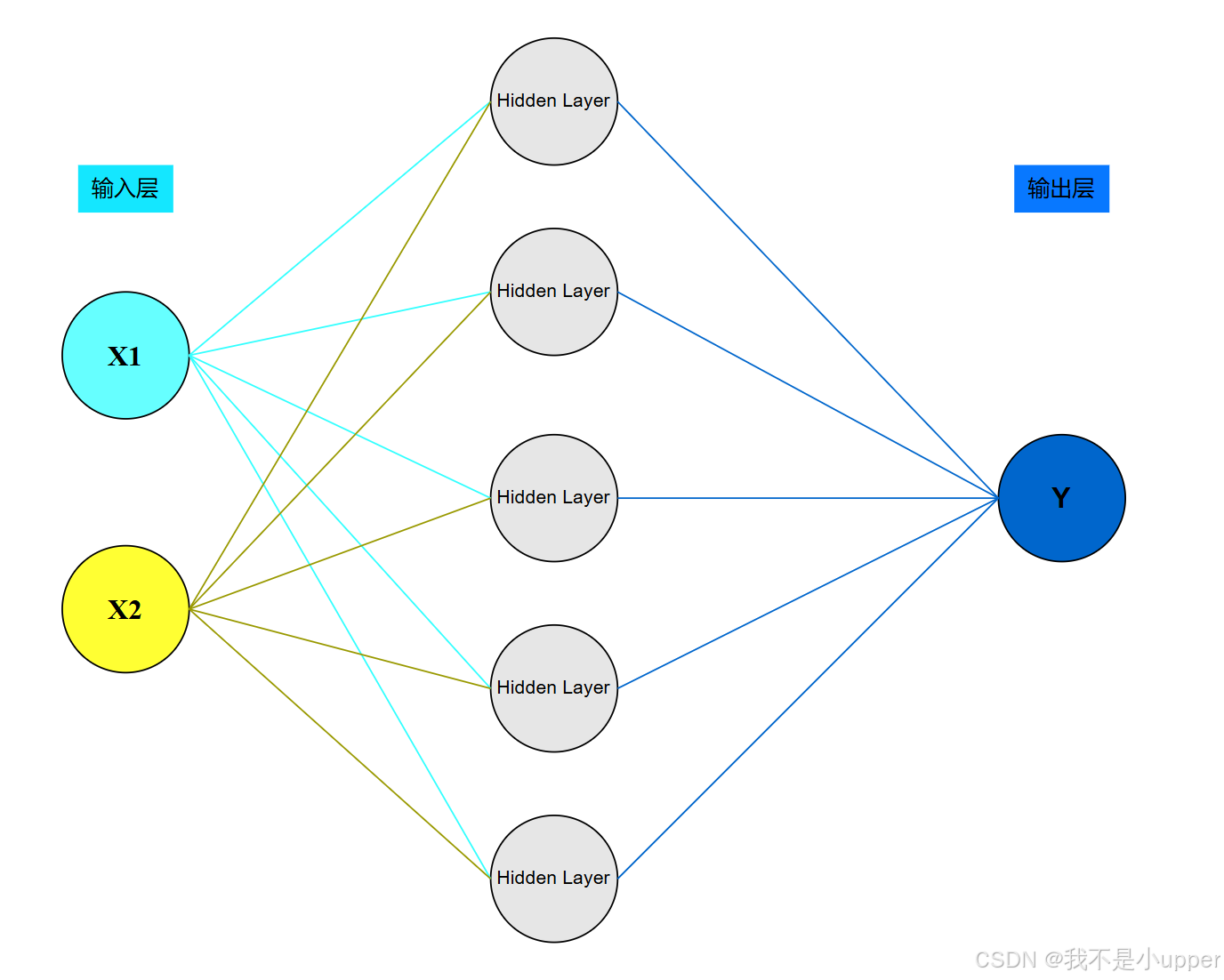
2. 导入必要库

import numpy as np  # 数值计算库
import matplotlib.pyplot as plt  # 可视化库

NumPy：提供了高效的数组操作和线性代数运算，是神经网络计算的基础
Matplotlib：用于数据的可视化，展示数据集和决策边界

2. 生成模拟数据集

np.random.seed(42)  # 固定随机种子保证可重复性
X = np.random.randn(200, 2) * 2  # 生成200个二维正态分布样本
y = np.logical_xor(X[:,0] > 0, X[:,1] > 0).astype(int)  # 异或逻辑生成标签

异或问题：经典非线性可分问题，用于测试神经网络的非线性拟合能力
数据分布：样本分布在四个象限，通过 XOR 操作生成红蓝两类
astype(int)：将布尔值转换为 0/1 整数标签

3. 初始化网络参数

input_size = 2       # 输入特征数
hidden_size = 5      # 隐藏层神经元数
output_size = 1      # 输出类别数
learning_rate = 0.1  # 学习率控制参数更新步长
epochs = 1000        # 迭代次数

W1 = np.random.randn(input_size, hidden_size) * 0.01  # 输入层到隐藏层权重
b1 = np.zeros((1, hidden_size))                      # 隐藏层偏置
W2 = np.random.randn(hidden_size, output_size) * 0.01 # 隐藏层到输出层权重
b2 = np.zeros((1, output_size))                      # 输出层偏置

随机初始化：小随机值避免神经元饱和（sigmoid 导数在 0 附近较大）
权重矩阵维度：输入层 2→隐藏层 5→输出层 1
偏置初始化：使用全零初始化（对称破缺在隐藏层权重中已通过随机值实现）
可能初学者的小伙伴有点困惑，为什么要*0.01，那是因为若权重未缩小（如直接使用 np.random.randn），则线性组合 z = XW + b 的结果可能很大，导致激活值处于饱和区，导数消失。乘以 0.01 后，z 值分布在 [-0.01, 0.01] 附近，此时sigmoid 函数处于近似线性区域（导数接近 0.25）见下表，这样就可以保证梯度传递更有效，避免训练停滞。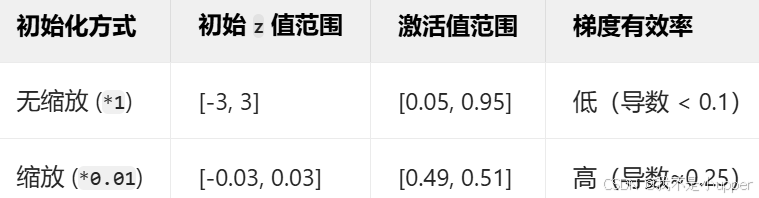

4. 定义激活函数及其导数

本次使用sigmoid激活函数，有些也称之为logistic函数，本次使用的sigmoid函数的输出范围限定在(0,1)之间，相当于做了归一化操作，可以用于将预测概率作为输出的模型,且sigmoid函数便于求导，计算量减小。其函数表达式为：

$sigmoid(x)=\frac{1}{1+e^{-x}}$

其导数为：

由于 $y = \sigma( z_{2})$ ，其中 $z_{2} = h\cdot W_{2}+b_{2}$ ，因此：

代码实现过程

def sigmoid(x):
    return 1 / (1 + np.exp(-x))  # Sigmoid函数公式

def sigmoid_derivative(output):
    return output * (1 - output)  # 链式法则形式的导数

Sigmoid 函数：将线性组合映射到 [0,1] 区间，适合二分类问题
导数优化：利用输出结果直接计算导数，避免重复计算exp

5. 前向传播过程

输入层 → 隐藏层

矩阵乘法：X (200×2) × W1 (2×5) = z1 (200×5)，偏置加法：z1 + b1 (1×5) → 广播为 (200×5)，激活函数：a1 = sigmoid(z1) → 非线性变换
隐藏层 → 输出层

矩阵乘法：a1 (200×5) × W2 (5×1) = z2 (200×1)，偏置加法：z2 + b2 (1×1) → 广播为 (200×1)，激活函数：a2 = sigmoid(z2) → 输出概率值
返回结果
返回中间结果 a1 和最终输出 a2，用于反向传播计算梯度
维度匹配验证

输入层：X (200, 2)，隐藏层：W1 (2, 5) → 每个输入特征连接到 5 个隐藏神经元。z1 (200, 5) → 每个样本生成 5 个隐藏激活值。输出层：W2 (5, 1) → 每个隐藏神经元连接到 1 个输出神经元。a2 (200, 1) → 每个样本生成 1 个概率预测值。
数学公式对应

隐藏层线性组合：

隐藏层激活：

输出层线性组合：

输出层激活：

以下是代码实现：

def forward(X):
    z1 = np.dot(X, W1) + b1   # 隐藏层线性组合：X * W1 + b1
    a1 = sigmoid(z1)         # 隐藏层激活值
    
    z2 = np.dot(a1, W2) + b2 # 输出层线性组合：a1 * W2 + b2
    a2 = sigmoid(z2)         # 最终输出概率
    
    return a1, a2            # 返回中间结果用于反向传播

矩阵乘法：np.dot实现批量样本的并行计算
维度说明：
- X: (200, 2) → z1: (200, 5) → a1: (200, 5)
- a1: (200, 5) → z2: (200, 1) → a2: (200, 1)

6. 定义损失函数

def cross_entropy_loss(y_pred, y_true):
    return -np.mean(y_true * np.log(y_pred + 1e-8) + (1 - y_true) * np.log(1 - y_pred + 1e-8))

交叉熵损失：
- 公式：
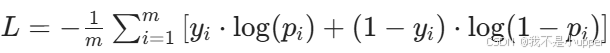
- 优势：对概率预测敏感，梯度稳定（避免 0 值导致 log 爆炸）
1e-8 平滑项：防止 log (0) 出现

7. 反向传播过程

流程图说明：

输入：
- 前向传播得到的隐藏层激活值 a1 和输出层激活值 a2
- 真实标签 y
输出层误差 δ²：
- 公式：δ² = (a2 - y) * a2 * (1 - a2)
- 意义：输出层预测值与真实值的差异乘以激活函数导数
隐藏层误差 δ¹：
- 公式：δ¹ = (δ²・W2^T) * a1 * (1 - a1)
- 意义：通过权重矩阵反向传播误差，再乘以隐藏层激活函数导数
输出层梯度：
- dW2：隐藏层到输出层的权重梯度
- db2：输出层偏置梯度
隐藏层梯度：
- dW1：输入层到隐藏层的权重梯度
- db1：隐藏层偏置梯度
参数更新：
- W2 = W2 - learning_rate * dW2
- b2 = b2 - learning_rate * db2
- W1 = W1 - learning_rate * dW1
- b1 = b1 - learning_rate * db1

关键数学关系：

链式法则：误差项通过权重矩阵反向传播
矩阵运算：
- δ² 维度：(200, 1)
- W2^T 维度：(1, 5)
- δ¹ 维度：(200, 5)
- a1^T 维度：(5, 200)
- dW2 维度：(5, 1)

下面是代码复现：

def backward(X, y, a1, a2):
    m = X.shape[0]  # 样本数量
    
    # 输出层误差
    delta2 = (a2 - y) * sigmoid_derivative(a2)  # δ² = (a² - y) * a²(1-a²)
    
    # 隐藏层误差
    delta1 = np.dot(delta2, W2.T) * sigmoid_derivative(a1)  # δ¹ = (W²^T δ²) * a¹(1-a¹)
    
    # 计算梯度
    dW2 = (1/m) * np.dot(a1.T, delta2)  # ∂L/∂W² = (1/m) a¹^T δ²
    db2 = (1/m) * np.sum(delta2, axis=0) # ∂L/∂b² = (1/m) Σδ²
    
    dW1 = (1/m) * np.dot(X.T, delta1)    # ∂L/∂W¹ = (1/m) X^T δ¹
    db1 = (1/m) * np.sum(delta1, axis=0) # ∂L/∂b¹ = (1/m) Σδ¹
    
    return dW1, db1, dW2, db2

误差项推导：
- 输出层：δ² = (a² - y) * σ’(z²)
- 隐藏层：δ¹ = (W²^T δ²) * σ’(z¹)
梯度计算：
- dW2：隐藏层激活到输出层的梯度
- dW1：输入到隐藏层的梯度
- 批量平均：所有梯度除以样本数 m

8. 训练循环

loss_history = []  # 记录损失变化

for epoch in range(epochs):
    # 前向传播
    a1, a2 = forward(X)
    
    # 计算损失
    loss = cross_entropy_loss(a2, y.reshape(-1, 1))
    loss_history.append(loss)
    
    # 反向传播
    dW1, db1, dW2, db2 = backward(X, y.reshape(-1, 1), a1, a2)
    
    # 更新参数
    W1 -= learning_rate * dW1
    b1 -= learning_rate * db1
    W2 -= learning_rate * dW2
    b2 -= learning_rate * db2
    
    # 打印进度
    if epoch % 100 == 0:
        print(f'Epoch {epoch}, Loss: {loss:.4f}')

参数更新：梯度下降法，参数沿梯度反方向更新
维度匹配：y 需要 reshape 为 (200,1) 以匹配 a2 的形状
损失记录：用于后续绘制损失曲线

9. 可视化决策边界

h = 0.02  # 网格精度
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

Z = np.c_[xx.ravel(), yy.ravel()]  # 生成网格点坐标
a1, a2 = forward(Z)                # 预测所有网格点
Z = (a2 > 0.5).astype(int).reshape(xx.shape)  # 转换为类别标签

plt.figure(figsize=(10, 7))
plt.contourf(xx, yy, Z, alpha=0.4)  # 绘制决策区域
plt.scatter(X[y==0,0], X[y==0,1], c='blue', label='Class 0')
plt.scatter(X[y==1,0], X[y==1,1], c='red', label='Class 1')
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('Neural Network Decision Boundary')
plt.legend()
plt.show()