N皇后问题

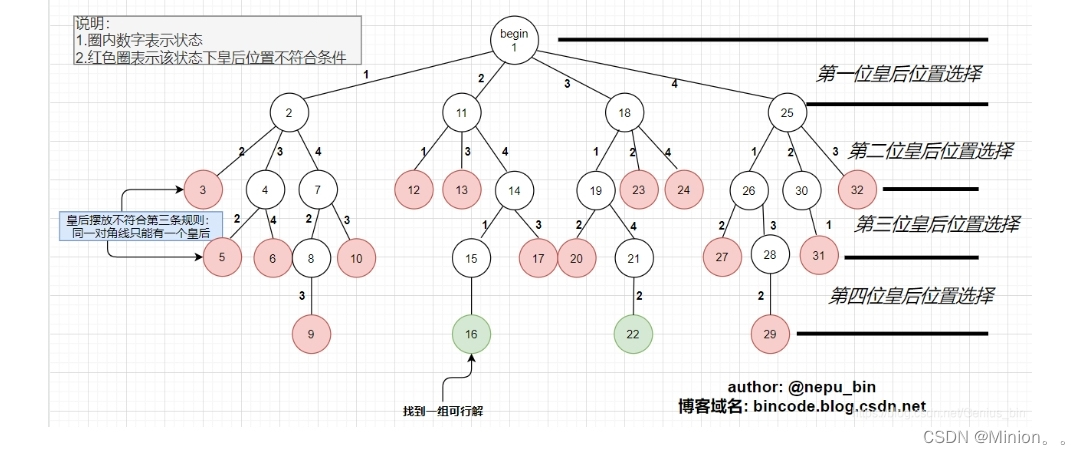
由于皇后的位置受到上述三条规则约束，我们必须通过一些技术手段来判断当前皇后的位置是否合法。

1.皇后的编号从 0 ~ N - 1 （N表示皇后的数量），这样编号的想法很简单：数组下标从0开始（这样方便后续对其位置的说明）。

2.使用一维数组 putInf 对每一行皇后的存放位置进行保存，因此得到解向量 (putInf[0], putInf[1], putInf[3], … , putInf[N - 1])，putInf[i] 表示第 i 个皇后被放置到了第 putInf[i] + 1 列上（putInf数组中存储的是列号，范围为 0 ~ N - 1）;

3.第二个条件：各皇后不同列， N 皇后放在 N x N 的棋盘上，那么每一列最多且必须放置一个皇后，这里我用了一个 used数组 对每一列的摆放情况进行记录， used[i] = true 表示 第 i 列 已经放置了皇后，used[i] = false 表示第i列暂未放置皇后，这样我们可以保证不在一列上放置多个皇后，也就能满足 各皇后不同列 的规则。

4.各皇后不能处于同一对角线位置：假设两皇后位置坐标分别为(i, j) 、（l, k），那么根据直线斜率公式：

(i - l) / (j - k) = 1 求解得 i - l == j - k ①
(i - l) / (j - k) = -1 求解得 i - l == k - j ②
这两种情况出现时表明处于同一对角线，那么要满足摆放规则就必须满足
| i - l | != | j - k | （“| |” 表示绝对值）

 完整代码

 
#include<stdio.h>
#include<malloc.h>
#include<math.h>
 
//判断把它放在这是是否是适用的 
 
int place(int *paraSolution,int paraT){
	int j;
	for(j = 0;j < paraT;j++){
		 if ((abs(paraT - j) == abs(paraSolution[j] - paraSolution[paraT])) || (paraSolution[j] == paraSolution[paraT]))
	return 0;
	}
	return 1;
}
 
//Backtracking.回溯。 
 
void backtracking(int* paraSolution,int paraN, int paraT){
	int i;
	if(paraT>paraN){
		for(i = 1;i <= paraN;i++)
		printf("%d",paraSolution[i]);
		printf("\r\n");
	}
	else
	{
		for(i = 1;i <= paraN;i++){
			paraSolution[paraT] = i;
			if(place(paraSolution,paraT))
			backtracking(paraSolution,paraN,paraT + 1);
		}
	}
}
 
//Title: n queens.<br>
 
void nQueen(int paraN){
	int i;
	int*solution = (int*)malloc((paraN + 1) * sizeof(int));
	for(i = 0;i <= paraN;i++)
	solution[i] = 0;
	
	backtracking(solution,paraN,1);
}
 
//The entrace.输出数据 
 
int main(){
	printf("输入个数： \r\n");
	int n;
	scanf("%d",&n);
	nQueen(n);//括号里面写具体有多少个元素 
	return 1;
}

运行结果

输入个数：
6
246135
362514
415263
531642