蓝桥OJ3362 建造房屋

蓝桥OJ3362 建造房屋

前言&废话

报名蓝桥省赛班后学动态规划遇到的第一个题目,当时不论是班里学长讲还是上网找攻略都看得朦朦胧胧的,最后想了三四个小时总算看懂了百分之八九十,现在我把我写这题遇到的一些错误写在这里,希望能帮到和我一样的动态规划小白.

官网题目

思路一

dp设置

设置dp[i][j]是前i条街道一共建造j个房子的方案数,那么
dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1]j-3]+…+dp[i-1][0];

举个例子

如果要在前4条街道建造一共7个房子,那么方案数是一下情况的和:

• 第四条街道建0个, 前三条街道建7个
• 第四条街道建1个, 前三条街道建6个
• 第四条街道建2个, 前三条街道建5个
• 第四条街道建3个, 前三条街道建4个
• 第四条街道建4个,前三条街道建3个
• 第四条街道建5个,前三条街道建2个
• 第四条街道建6个,前三条街道建1个
• 第四条街道建7个,前三条街道建0个
  删去的部分不满足每条街道至少一个房屋的要求,可以在数组中设置为0.

AC代码

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

ll mod = 1e9 + 7;
ll dp[55][2605];//dp[i][j]表示只考虑前i条街道，总共建造j个房屋的方案数
int main()
{
    int N,M,K;
    cin >>N>>M>>K;
    auto show=[&](){//用于打印表格,便于调试
        cout<<"------\n";
        for(int i=0;i<=N;i++){
            for(int j=0;j<=M;j++){
                cout<<dp[i][j]<<"\t";
            }
            cout<<"\n";
        }
    };
    dp[0][0]=1;
    for(int i=1;i<=N;i++){//考虑前1到前N条街道
        for(int j=i;j<=K;j++){//一共建造j个房屋,因为每条街道至少一个房屋,所以j从i开始
            for(int thisnum=1;thisnum<=M&&thisnum<=j;thisnum++){
                int prenum=j-thisnum;
                //thisnum:第i条街道建造房屋数,至少为1
                //prenum:此时前i-1条街道建造房屋数
                dp[i][j]+=dp[i-1][prenum];
                dp[i][j]%=mod;
            }
//            cout<<"i:"<<i<<" j:"<<j;
//            show();
        }
    }
    int ans =0;
    for(int j=1;j<=K;j++){
        ans+=dp[N][j];//
        ans%=mod;
    }
    cout<<ans;
    return 0;
}

dp表格样例

以样例2 3 5为例

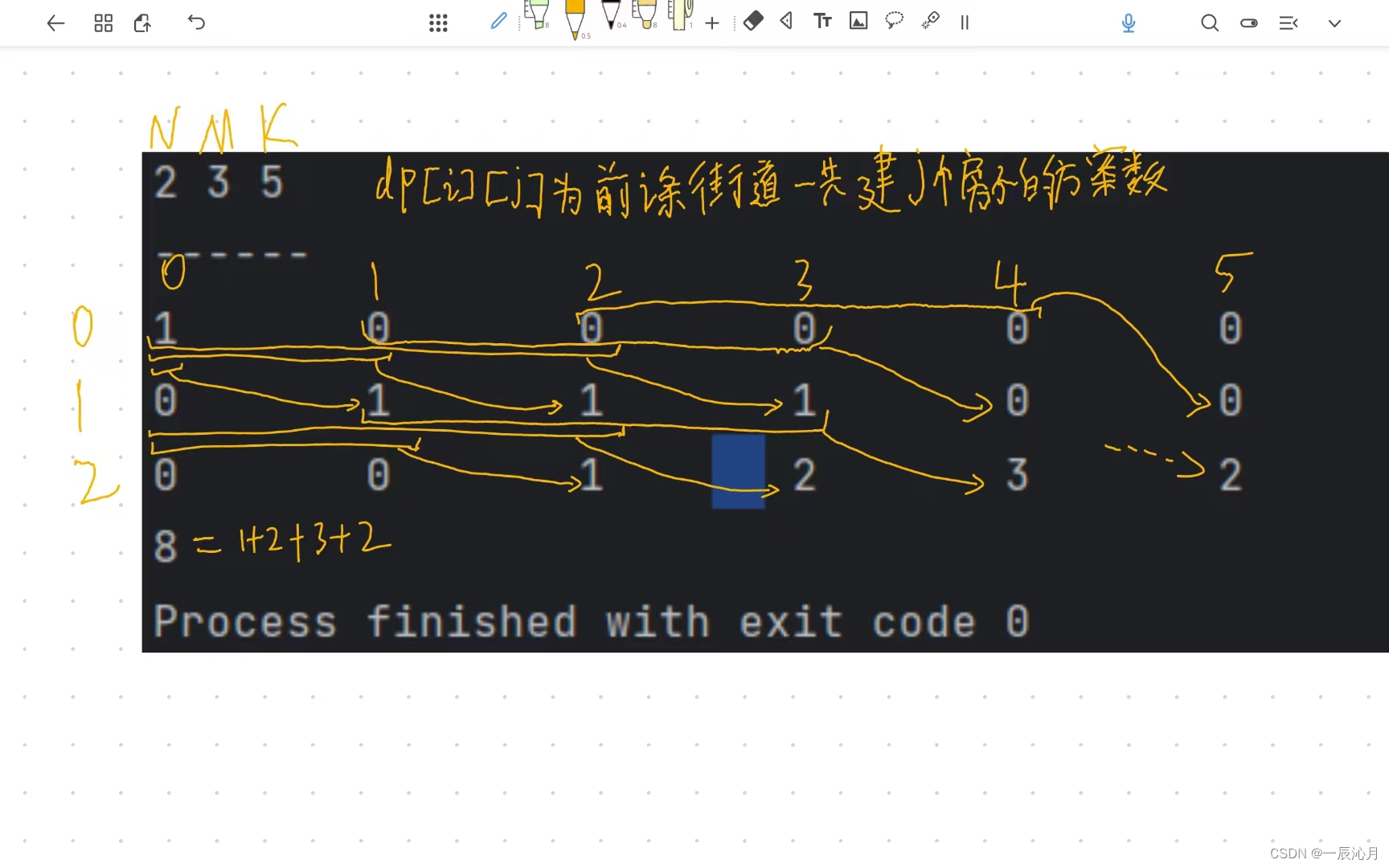
由图可知
dp[1][1]=dp[0][0]+dp[0][1]
dp[1][2]=dp[0][0]+dp[0][1]+dp[0][2]
dp[1][3]=dp[0][1]+dp[0][2]+dp[0][3]
…
dp[2][2]=dp[1][0]+dp[1][1]
…
以此类推

坑

1. 由于题目问的是不超过K元的建造方案,所以求到最后第N行是要把所有方案数加起来,才是答案.
2. 这道题有两种动态规划的思路:一种是枚举建造j个房屋再把所有方案求和,就是上面的代码;另一种是直接设置数组的时候就设置dp[i][j]为前i条街道建造不超过j个房屋的方案数.由于我当时把学长的代码和其他人的题解混着看,所以看了好久才明白用的不是同一个思路.
3. 我们当时有两节课,一节叫线性dp,一节叫二维dp,这道题在线性dp的练习题中,然后我以为用一维dp数组就可以解决,想了半天也没想出来.

思路二

dp设置

dp[i][j]设置为前i条街道,建造不超过j个建筑的方案数,状态转移和上面是一样的dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1]j-3]+…+dp[i-1][0];

举个例子 注意关键词 不超过

如果要在前4条街道建造一共不超过7个房子,那么方案数是一下情况的和:

• 第四条街道建0个, 前三条街道建不超过7个
• 第四条街道建1个, 前三条街道建不超过6个
• 第四条街道建2个, 前三条街道建不超过5个
• 第四条街道建3个, 前三条街道建不超过4个
• 第四条街道建4个,前三条街道建不超过3个
• 第四条街道建5个,前三条街道建不超过2个
• 第四条街道建6个,前三条街道建不超过1个
• 第四条街道建7个,前三条街道建不超过0个
  删去的部分不满足每条街道至少一个房屋的要求
  两种思路的状态转移方程是一样的,区别在于初始化,第一种思路只初始化dp[0][0]=1;而第二种(本方法)要初始化第0行全为1,可以认为是dp[0]的前缀和,因为第二种思路的dp数组,就是第一种思路的dp数组的前缀和
  直观地看,建造不超过k个房子的方案数,就是建0个+建1个+建2个+建3个+…+建k个

AC代码

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

ll mod = 1e9 + 7;
ll dp[55][2605];//dp[i][j]表示只考虑前i条街道，总共建造j个房屋的方案数

int main()
{
    int N,M,K;
    cin >>N>>M>>K;
    for(int i=0;i<= K;i ++)dp[0][i]=1;//初始化,便于后续递推
    for(int i=1;i<=N;i++)//依次考虑前1~N条街道
    {
        for(int j=i;j<=K;j++){//前i条街道一共建造不超过j个房屋,且j>=i
            for(int k=1;k<=M&&k<=j;k++){//当前街道建造k个,前i-1条街道建造不超过j-k个
                dp[i][j]=(dp[i-1][j-k]+dp[i][j])%mod;
            }
        }
    }
    cout << dp[N][K] << endl;//dp[N][K]即在前N条街道，总共建造不超过K个房屋的方案数
    return 0;
}

滚动数组

以思路1为例
可以滚,会零一背包的滚动应该就能会这道题的滚动

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

ll mod = 1e9 + 7;
ll dp[2][2605];//dp[i][j]表示只考虑前i条街道，总共建造j个房屋的方案数
int main()
{
    int N,M,K;
    cin >>N>>M>>K;
    auto show=[&](){
        cout<<"------\n";
        for(int i=0;i<2;i++){
            for(int j=0;j<=K;j++){
                cout<<dp[i][j]<<"\t";
            }
            cout<<"\n";
        }
    };
    dp[0][0]=1;
    for(int i=1;i<=N;i++){//考虑前1到前N条街道
        for(int j=i;j<=K;j++){//一共建造j个房屋,因为每条街道至少一个房屋,所以j从i开始
            for(int thisnum=1;thisnum<=M&&thisnum<=j;thisnum++){
                int prenum=j-thisnum;
                //thisnum:第i条街道建造房屋数,至少为1
                //prenum:此时前i-1条街道建造房屋数
                dp[1][j]+=dp[0][prenum];
                dp[1][j]%=mod;
            }

        }
        swap(dp[0],dp[1]);//将最新一行放到上面
        for(int j=0;j<=K;j++){//清空下面那行
            dp[1][j]=0;
        }
    }
//    show();
    ll ans =0;
    for(int j=1;j<=K;j++){
        ans+=dp[0][j];//由于每次计算完都会交换上下行,所以dp[0]才是最终计算完的那一行;
        ans%=mod;
    }
    cout<<ans;
    return 0;
}

可能有更简单的滚动方法,但是太累了,不想了

前缀和优化

由于两种思路的dp[i][j]都与第i-1行的区间和有关,所以可以使用前缀和优化.
注意由于思路二的dp数组是思路一的dp数组的前缀和,如果在思路二使用前缀和优化,相当于思路一dp的二次前缀和,容易眼花缭乱.
前缀和优化就是把最内层的for循环假发换成使用i-1行的前缀和数组相减.要加上区间[l,r]其实就可以简单理解为prenum的最大值和最小值,最后注意一下输出的时候有可能dp[0][N]在加上dp[0][N-1]后取了模,所以要判断一下.

思路二,前缀和优化代码

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

ll mod = 1e9 + 7;
ll dp[2][2605];//dp[i][j]表示只考虑前i条街道，总共建造不超过j个房屋的方案数
int main()
{
    int N,M,K;
    cin >>N>>M>>K;
    auto show=[&](){
        cout<<"------\n";
        for(int i=0;i<2;i++){
            for(int j=0;j<=K;j++){
                cout<<dp[i][j]<<"\t";
            }
            cout<<"\n";
        }
    };
for(int i=0;i<K;i++){
    dp[0][i]=1;
}//思路二基本的初始化
for(int i=1;i<=K;i++){
    dp[0][i]+=dp[0][i-1];
}//使用前缀和的初始化

    for(int i=1;i<=N;i++){//考虑前1到前N条街道
        for(int j=i;j<=K;j++){//一共建造不超过j个房屋,因为每条街道至少一个房屋,所以j从i开始
            int l=j-min(M,j);
            int r=j-1;
            // l,r分别是prenum最大值和最小值
//            for(int thisnum=1;thisnum<=M&&thisnum<=j;thisnum++){
//                int prenum=j-thisnum;
//                thisnum:第i条街道建造房屋数,至少为1
//                prenum:此时前i-1条街道建造房屋数
//                dp[1][j]+=dp[0][prenum];
//                dp[1][j]%=mod;
//            }
            if(l==0)
                dp[1][j]=dp[0][r];
            else
                dp[1][j]=dp[0][r]-dp[0][l-1];
            dp[1][j]+=dp[1][j-1];
            dp[1][j]%=mod;
        }
//      show();
        //滚动数组
        swap(dp[0],dp[1]);
        for(int j=0;j<=K;j++){
            dp[1][j]=0;
        }
        //
    }
//    show();
ll ans=dp[0][K]-dp[0][K-1];
    if(ans<0)ans+=mod;
    cout<<ans;
    return 0;
}

未解决的问题

不知道思路一的初始化为什么是dp[0][0]=1,只能说是试出来的.如果有人能解释为什么的话,欢迎留言